poj 2653 Pick-up sticks（线段相交）

随机线段堆叠问题的解决方案

最新推荐文章于 2020-06-24 20:37:33 发布

原创最新推荐文章于 2020-06-24 20:37:33 发布 · 681 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#numbers #input #each #random #output

计算几何专栏收录该内容

67 篇文章

订阅专栏

本博客探讨了一个涉及随机线段堆叠并找出顶部线段的问题。通过输入线段的数量及其坐标，读者可以了解如何识别那些未被其他线段覆盖的线段。文章详细解释了输入格式、数据限制及输出要求，并提供了使用暴力搜索方法解决此问题的代码示例。

Pick-up sticks

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 6686		Accepted: 2450

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.

Output

For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.

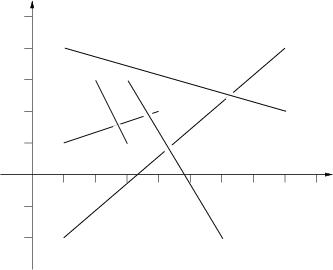
The picture to the right below illustrates the first case from input.

Sample Input

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

Hint

Huge input,scanf is recommended.

Source

Waterloo local 2005.09.17

题目： http://poj.org/problem?id=2653

题意：随机n条线段，按顺序叠放，要求那些线段不被其他线段叠压

分析：本来一看数据以为要用扫描线那个判断线段相交的方法，不过偷偷搜了下题解，居然都是暴力过的= =，我也跟着水一个哈

代码：

#include<cstdio>
#include<iostream>
using namespace std;
const int mm=111111;
typedef double mType;

/**表示点或向量*/
struct Tpoint
{
    mType x,y;
    Tpoint(){}
    Tpoint(mType _x,mType _y):x(_x),y(_y){}
};


/**有起点和终点的向量或线段*/
struct Tsegment
{
    Tpoint start,end;
    Tsegment(){}
    Tsegment(Tpoint _start,Tpoint _end):start(_start),end(_end){}
    Tsegment(mType sx,mType sy,mType tx,mType ty):start(sx,sy),end(tx,ty){}
};


/**生成一个点P到点Q的向量*/
Tpoint MakeVector(Tpoint P,Tpoint Q)
{
    return Tpoint(Q.x-P.x,Q.y-P.y);
}

/**向量P与Q的叉积PQ*/
mType CrossProduct(Tpoint P,Tpoint Q)
{
    return P.x*Q.y-P.y*Q.x;
}

/**向量QP与向量QR的叉积，用来判断向量的拐向
*  返回值: >0 向右拐, <0 向右拐,等于零同向或反向
*/
mType MultiCross(Tpoint P,Tpoint Q,Tpoint R)
{
    return CrossProduct(MakeVector(Q,P),MakeVector(Q,R));
}

/**判断线段P和线段Q是否相交*/
bool IsIntersect(Tsegment P,Tsegment Q)
{
    if(max(P.start.x,P.end.x)<min(Q.start.x,Q.end.x)||max(Q.start.x,Q.end.x)<min(P.start.x,P.end.x)||
       max(P.start.y,P.end.y)<min(Q.start.y,Q.end.y)||max(Q.start.y,Q.end.y)<min(P.start.y,P.end.y))return 0;
    return (MultiCross(P.end,P.start,Q.start)*MultiCross(P.end,P.start,Q.end)<0&&
            MultiCross(Q.end,Q.start,P.start)*MultiCross(Q.end,Q.start,P.end)<0);
}
Tsegment g[mm];
int main()
{
    int i,j,n;
    mType sx,sy,ex,ey;
    while(scanf("%d",&n),n)
    {
        for(i=1;i<=n;++i)
        {
            scanf("%lf%lf%lf%lf",&sx,&sy,&ex,&ey);
            g[i]=Tsegment(sx,sy,ex,ey);
        }
        printf("Top sticks:");
        for(i=1;i<n;++i)
        {
            for(j=i+1;j<=n;++j)
                if(IsIntersect(g[i],g[j]))break;
            if(j>n)printf(" %d,",i);
        }
        printf(" %d.\n",n);
    }
    return 0;
}