滤波器开发之四：基于算术平均的中值滤波器

  在信号采集系统中，除了我们感兴趣的数据外，难免会有一些来自于环境的干扰信号。但我们总希望我们得到的数据是纯净而真实的，为了达到这个目标，我们不得不想办法去除这些干扰信号，于是滤波器就成为我们必不可少的帮手。这一篇我们就来讨论如何通过软件实现基于中值平均算术平均算法的中值数字滤波器。

1、问题的提出

  在我们通过AD采集获取数据时，不可避免会受到干扰信号的影响，而且很多时候我们希望尽可能的将这种影响减到最小。为实现这一目的，人们想了很多办法，有硬件方面的，也有软件方面的。在硬件难以改变或者软件能够达到相应效果时，我们一般采用软件方法来实现，通常称之为数字滤波。
  在我们的项目中，要求100毫秒采集100个数据，由于信号非常微弱，很容易收到干扰，所以实际采集到的数据中起伏很大，这其中有很多数据数叠加了干扰项的数据。通过示波器观察，我们发现在这些干扰项中，有周期性的频率相对低一些的干扰，也有无规律的频率很高的干扰。这些干扰信号对我们的测量结果的影响非常之大，几乎让测量结果完全不可信，所以我们必须想办法将其去除。
  我们考虑并测试了多种滤波算法，我们发现单一的滤波手段很难同时滤掉几种不同的干扰信号。所以我们尝试组合多种滤波算法以实现我们的目标。

2、算法设计

  前面我们已经描述了问题的来源，所以为了去除不同种类的干扰信号，我们必须设计一个针对多种干扰信号的滤波算法。我们知道主要的干扰信号是相对频率较低的周期干扰和相对频率较高的非周期干扰，我们将分析这两种信号的特点并针对性的采取相应的滤波手段。
  首先我们来考虑相对频率较低的周期干扰，这种干扰来自于环境并且很难避免，但这种干扰信号具有一定的规律，所以它对正常信号造成的影响也是有一定规律的。我们可以图示如下：

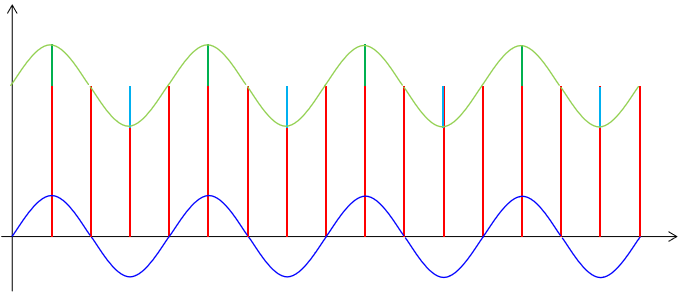
  如果只存在这一种周期性的低频率的干扰信号，那么我们很容易想到采用算术平局算法就能够去除，在前面我们也确实是这么做的。事实上如果存在多种频率的周期性干扰信号，只要采集到的数据样本数量足够，采用算数平均算法基本都是可以得到比较理想的结果。在我们的项目中，我们的采集频率达到了1KHz，而我们每100毫秒出一个数，所以从理论上讲，10Hz以上的周期性干扰都可以通过算术平均率波来消除。
  接下来我们来考虑相对频率较高的非周期干扰，这种干扰具有较大的随机性，有可能对信号的影响较大，也有可能对信号的影响较小，其频率和幅值都是随机的，测量结果存在很大的偶然性。我们可以简单的图示如下：

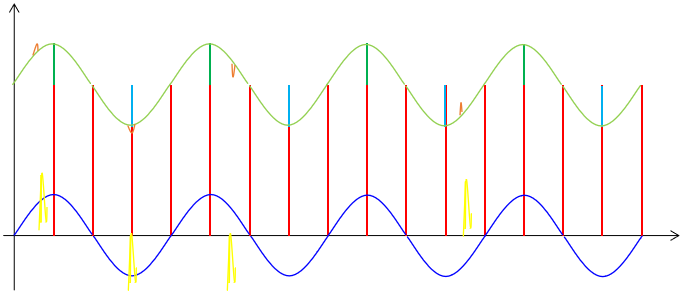
  对于这种干扰我们前面的方法对他是没有效果的，但我们的ADC采用的是积分方式来检测信号的，所以在两个采样点之间，无论这类干扰信号在何时出现都会叠加到紧接着的这个采样数据上，致使最终的采样数据比周期性干扰叠加的情况下要么大一些，要么小一些。这就存在两种情况，如果是正向干扰就会是数据变大一些，如果是反向干扰就会是数据变小一些。使得最终的测量数据更加背离原始数据或者更加接近原始数据。
  对于更加接近我们需要的数据的变化，我们先不用理会它，毕竟它更加接近我们想要的数据。对于更加偏离的那一部分数据，我们有什么办法将其去除掉呢？办法是有的，我们借鉴比赛积分中去掉偶然性的方式，去掉最高和最低的数，中间的数应该更接近与真实值。具体如下图所示：