三分

【例题引入】

例题传送门三分法

题目大意：给出一个N次函数，保证在范围 [ l，r ] 内存在一点x，使得 [ l，x ] 上单调增，[ x，r ] 上单调减。试求出x的值。（洛谷 3382）

这道题，若没学三分，第一个想法应该是用二分，但是二分出来的答案不好判断是否合法（至少本蒟蒻不知道怎么判断）

这个时候我们想到三分，三分法一般适用于求单峰函数极值的一些东西

 

【基本思想】

其实三分和二分的做法差不多，只不过二分是找 [ l，r ] 间的中点，三分是找 [ l，r ] 间的三等分点

那么 m1 = l + ( r - l ) / 3 , m2 = r - ( r - l ) / 3

我们将两个点中更优的点叫做好点（若计算单峰函数的最大值，则函数值更大的那个点就为好点；若计算单峰函数的最小值，则函数值更小的那个点就为好点），另一个叫做坏点，如下图：

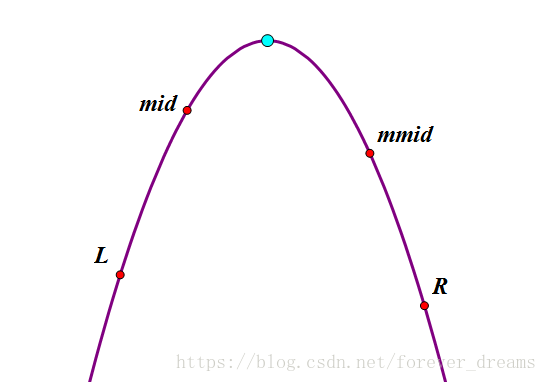
上图中，我们用 m1 代替 mid，m2 代替 mmid

很显然，m1 是好点，m2 是坏点

又因为在 [ l，r ] 中这是单峰函数，所以最优点和好点应在坏点同侧（可以自己画图理解），那缩小范围的时候就把 r 改成 m2 ，即我们的求解区间从 [ l，r ] 变为 [ l，m2 ] ，不断缩小范围直到求出解

 

【代码】

（其实三分不是一种常用的算法，大家了解一下就行了）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const double eps=1e-12;
int n;
double a[15],w[15];
double f(double x)
{
	int i;
	double pow=1,ans=0;
	for(i=n+1;i>=1;--i)
	{
		ans+=a[i]*pow;
		pow*=x;
	}
	return ans;
}
int main()
{
	int i;
	double l,r,m1,m2;
	scanf("%d",&n);
	scanf("%lf%lf",&l,&r);
	for(i=1;i<=n+1;++i)
	  scanf("%lf",&a[i]);
	while(r-l>=eps)
	{
		m1=l+(r-l)/3;
		m2=r-(r-l)/3;
		if(f(m2)-f(m1)>=eps)
		  l=m1;
		else
		  r=m2;
	}
	printf("%.5lf",l);
	return 0;
}