LeetCode96. 不同的二叉搜索树

皮卡猴

于 2021-11-08 21:21:36 发布

阅读量102

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode刷题文章标签： leetcode 动态规划算法

本文链接：https://blog.youkuaiyun.com/flying_monkey_1/article/details/121216187

leetcode刷题专栏收录该内容

252 篇文章

订阅专栏

这篇博客详细介绍了如何使用动态规划解决LeetCode96题，即计算不同结构的二叉搜索树的数量。通过分析元素作为头结点时，左子树和右子树的可能情况，得出递推公式并实现代码，有效地求解了问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCode96. 不同的二叉搜索树

1. 问题描述

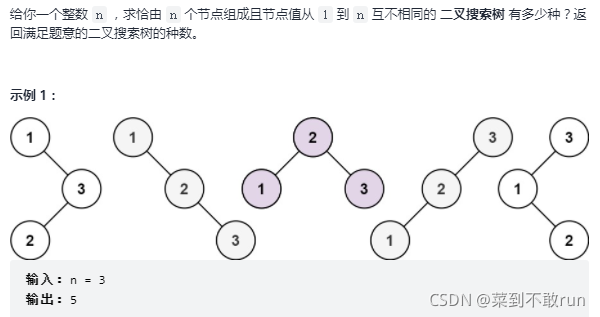
在这里插入图片描述

2. 思路

动态规划

dp[3]，就是元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3. 代码

func numTrees(n int) int {
    dp := make([]int, n + 1)
    dp[0], dp[1] = 1, 1

    for i := 2; i < n + 1; i++ {
        for j := 1; j < i + 1; j++ {
            dp[i] += dp[j-1] * dp[i-j]
        }
    }
    return dp[n]
}