神经网络中的激活函数

原创于 2019-08-17 17:08:55 发布 · 197 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#激活函数 #Sigmoid #ReLu

Deep Learing 专栏收录该内容

5 篇文章

订阅专栏

本文探讨了在神经网络中使用非线性激活函数的重要性，包括阶跃函数、Sigmoid函数和ReLU函数，并通过Python代码展示了这些函数的图形表现。

为了发挥叠加层所带来的优势，激活函数必须使用非线性函数

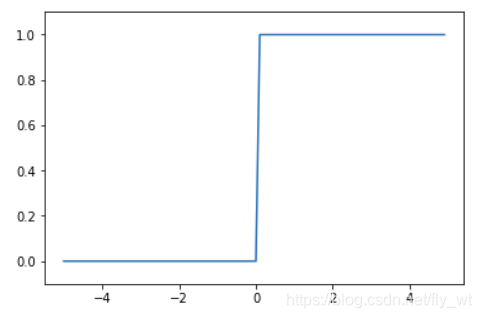
阶跃函数

import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
    return np.array(x > 0, dtype=int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

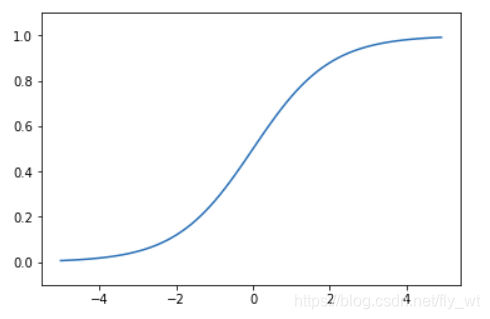
在这里插入图片描述

Sigmoid函数

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

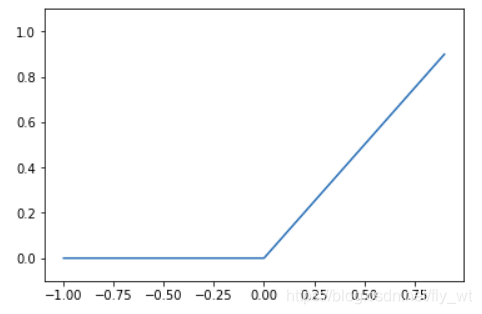
在这里插入图片描述

ReLu函数

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-1.0, 1.0, 0.1)
y = ReLU(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

在这里插入图片描述