【浮*光】 #树状数组# 洛谷P2161 [SHOI2009]会场预约

题目大意

• 设计一个数据结构，支持两种操作：
• 1. A i j 添加一个新的预约[i,j]，并删除所有与其冲突的预约。
• 返回此次操作删除的预约的个数。2. B 返回当前的预约总数。

方法分析

A操作的真实目的：查询一个区间中有多少种颜色。

并且清空所有在该区间中的颜色，把区间修改成另一种颜色。

因为任何时候区间的末端、都会随始端递增而递增，所以可以用差分的方法。

用树状数组维护【始端个数】的前缀和：

void add(int st,int k) //可以看做是区间修改
{ for(;st<maxn;st+=st&-st) c[st]+=k; }
//即：使用差分的思路，把区间的状态全部记录在始端上

之后就可以二分查找小于等于当前加入日程的末端的、最近的始端。

二分的代码是：

for(int p;p=ask(ed);){ //多次循环，删去所有相交的区间
//p存ed之前的始端个数，即最后一种颜色的编号
    int l=0,r=ed;
    while(l<r){ //二分找到最后可能交叉的区间
        int mid=(l+r)>>1; //就是当前区间和前一个区间是否有交集
        if(query(mid)<=p-1) l=mid+1; //寻找始端个数为p-1的位置
        else r=mid; //那个位置就是前一个区间的始端
    } if(endd[l]<st) break; //该区间在st之前就结束了
      else add(l,-1),cuts++,ans--;
}

这个过程可以看成是：

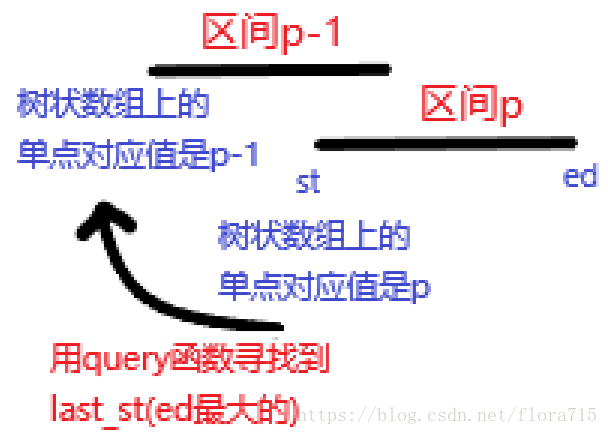
知道始端的位置后，我们可以得到相应的末端，如果形成相交就删去这个区间。

（其实这里就只用删去树状数组中始端的1了）。

因为始末端的单调性，当查找出的区间不形成相交就可以停止了。

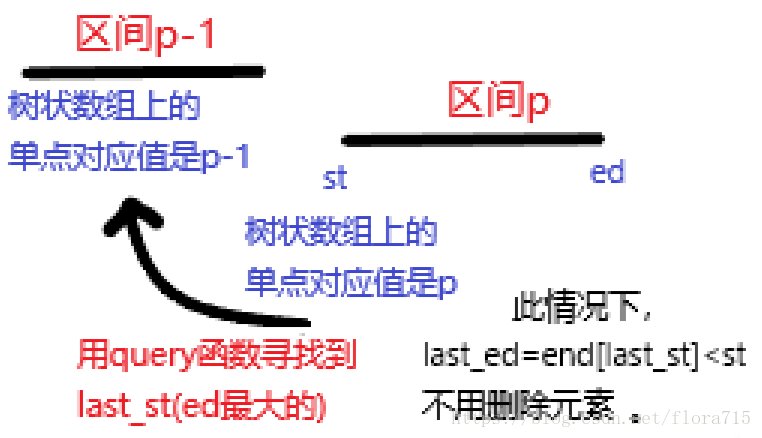
所以查询的query函数可以写出来：

int query(int x) //单点查询，可以看做区间修改时用了【差分】的思路
{ int sum=0; for(;x;x&=x-1) sum+=c[x]; return sum; }

注意输入输出即可，详细代码如下。

代码实现

#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#include<set>
#include<vector>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;

/*【p1198】会场预约
设计一个数据结构，支持两种操作：
1. A i j 添加一个新的预约[i,j]，并删除所有与其冲突的预约。
返回此次操作删除的预约的个数。 2. B 返回当前的预约总数。 */

/*【分析】
A操作的真实目的：查询一个区间中有多少种颜色，
清空数列中所有在该区间中出现的颜色，最后把这个区间修改成另一种颜色。
【在任何时候区间的末端随区间的始端递增而递增。】
考虑树状数组维护【始端个数】的前缀和。之后就可以二分查找小于等于某个点最近的始端。
知道始端的位置后，我们可以得到相应的末端，如果形成相交就删去这个区间（其实就是删去始端）。
因为始末端的单调性，当查找出的区间不形成相交就可以停止了。 */

const int maxn=100001;
int c[maxn],endd[maxn]; //管理数组c，ends记录每个始端对应的末端

void add(int st,int k) //可以看做是区间修改
//即：使用差分的思路，把区间的状态全部记录在始端上
{ for(;st<maxn;st+=st&-st) c[st]+=k; }

int query(int x) //单点查询，可以看做区间修改时用了【差分】的思路
{ int sum=0; for(;x;x&=x-1) sum+=c[x]; return sum; }

int main(){
    int n,ans=0; scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("\n"); 
        if(getchar()=='A'){
            int st,ed,cuts=0;
            scanf("%d%d",&st,&ed);
            for(int p;p=query(ed);){ //多次循环，删去所有相交的区间
            //p存ed之前的始端个数，即最后一种颜色的编号
                int l=0,r=ed;
                while(l<r){ //二分找到最后可能交叉的区间
                    int mid=(l+r)>>1; //就是当前区间和前一个区间是否有交集
                    if(query(mid)<=p-1) l=mid+1; //寻找始端个数为p-1的位置
                    else r=mid; //那个位置就是前一个区间的始端
                } if(endd[l]<st) break; //该区间在st之前就结束了
                  else add(l,-1),cuts++,ans--;
            } add(st,1); endd[st]=ed; ans++; //树状数组维护始端个数前缀和
            printf("%d\n",cuts);
        } else printf("%d\n",ans);
    } return 0;
}

 

 

                                              ——时间划过风的轨迹，那个少年，还在等你。