10.排序(上)

于 2019-01-13 21:57:25 发布
阅读量318 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： 数据结构与算法 数据结构学习笔记 文章标签： 排序 冒泡 插入 选择
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/firemaple_li/article/details/86439041
本文深入讲解排序算法的分析方法，包括执行效率、内存消耗及稳定性，详细解析冒泡排序、插入排序与选择排序的实现原理、代码实现及复杂度分析。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

1. 如何分析一个排序算法

1.1 排序算法的执行效率

1.1 最好、最坏、平均情况时间复杂度

1.2 时间复杂度的系数、常数、低阶

1.3 比较和交换(移动)的次数

1.2 排序算法的内存消耗

​ 原地排序 指特定空间复杂度是O(1)的排序算法

1.3 排序算法的稳定性

​ 稳定性 指待排序中有相等的元素，排完序后，这些元素的相对顺序不变。比如说现在按订单金额先排序，然后在按下单时间早晚排序。现有两个订单的金额相同，但是下单的时间不同。如果采用稳定排序可以这样：先按下单时间早晚排序，然后在按订单金额进行稳定排序。

2. 冒泡排序

2.1 思路

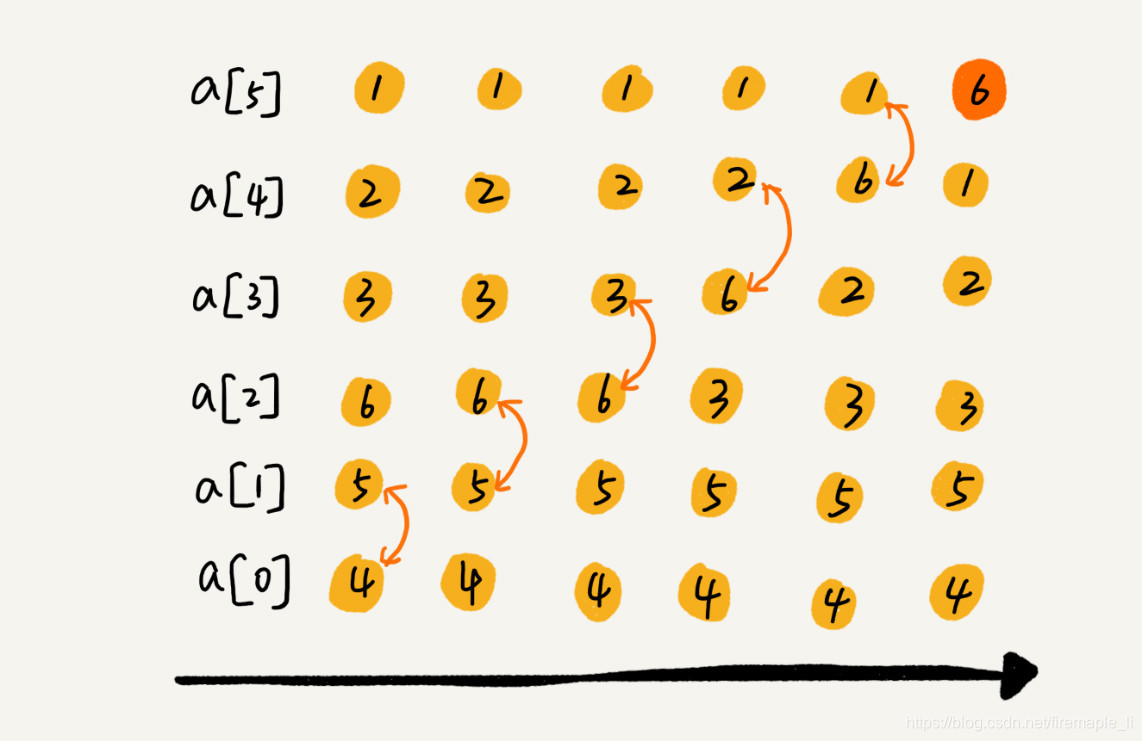
​ 冒泡排序只会比较相邻的元素，如果不满足大小要求，就进行交换，一次交换，就能使他移动到应该的位置，经过n次交换，排序完成。

在这里插入图片描述

2.2 代码

/**
     * 冒泡:
     * 最好: 经过优化，只冒一次泡，发现无元素交换，终止.为 O(n).
     * 最坏：已经有序，但是排序要求是其反方向排列。n+(n-1)+...+1 = ((n-1)/2)*n -> O(n²).
     * 平均：n*(n-1)/4 -> O(n²)
     *  有序度：是指数组中具有有序关系得元素对的个数。数学表达式：《br
     有序元素对：a[i] <= a[j],如果 i < j, 比如 3,4,1 有序度为1, 只有 (3,4)这个有序对.
     对于一个完全由序的数字，比如 1,2,3,4;有序度为 n(n-1)/2,, 也即是6，把这种完全有序的数字叫做 满有序度

     逆序度正好与有有序度相反，有序度=满有序度-逆序度，排序的过程，没交换一次，有序度+1，逆序-1，
     当有序度达到满有序度，排序完成 这个也印证了，如果有序度为0，排一次序，需要交换 (n-1) + (n-2) + ... + 1 = n*(n-1)/2 ，
     也就是满有序度的数量. 对于平均复杂度而言，取中间值 ( n(n-1)/2 + 0 )/ 2= n(n-1)/4，
     也就是说平均需要交换 n*(n-1)/4次. 比较的次数为肯定要多于交换的次数, 但上限为O(n²)，因此为O(n²).

     * @param arr
     */
    public static void bubble(int[] arr) {
        for(int i=0; i<arr.length; i++) {
            for(int j=0; j<arr.length - i - 1; j++) {
                if(arr[j] > arr[j+1]) {
                    int t = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = t;
                }
            }

            print(arr);
        }
        print(arr);
    }

优化：如果某次冒泡，无交换，说明排序完成:

/**
     * 优化：如果某次冒泡，无交换操作，说明已经有序了.
     * @param arr
     */
    public static void bubble_optimize(int[] arr) {
        for(int i=0; i<arr.length; i++) {
            boolean flag = false;

            for(int j=0; j<arr.length - i - 1; j++) {
                if(arr[j] > arr[j+1]) {
                    int t = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = t;

                    flag = true;
                }
            }

            if(!flag) {
                break;
            }

            print(arr);
        }
        print(arr);
    }

2.3 算法分析

2.3.1 是否原地排序

​ 排序过程只涉及相邻元素的交换，只需要申请常量级别的临时空间？(可能最坏设计n!次交换与)，因此是原地排序.

2.3.2 是否稳定

​ 如果两个元素相等， 可以不交换，因此可以为为稳定排序

2.3.2 时间复杂度

​ 有序度：是指数组中具有有序关系得元素对的个数。数学表达式：
有序元素对：a[i] <= a[j],如果 i < j, 比如 3,4,1 有序度为1, 只有 (3,4)这个有序对. 对于一个完全由序的数字，比如 1,2,3,4;有序度为 n(n-1)/2, 也即是6，把这种完全有序的数字叫做 满有序度

​ 逆序度正好与有有序度相反，有序度=满有序度-逆序度，排序的过程，没交换一次，有序度+1，逆序-1，当有序度达到满有序度，排序完成 这个也印证了，如果有序度为0，排一次序，需要交换 (n-1) + (n-2) + ... + 1 = n*(n-1)/2 ，也就是满有序度的数量. 对于平均复杂度而言，取中间值 ( n*(n-1)/2 + 0 )/ 2= n*(n-1)/4，也就是说平均需要交换 n(n-1)/4*次. 比较的次数为肯定要多于交换的次数, 但上限为O(n²)，因此为O(n²).

  • 平均：n*(n-1)/4 -> O(n²)

  • 最好: 经过优化，只冒一次泡，发现无元素交换，终止.为 O(n).

  • 最坏：已经有序，但是排序要求是其反方向排列。n+(n-1)+…+1 = ((n-1)/2)*n -> O(n²).

3. 插入排序

3.1思路

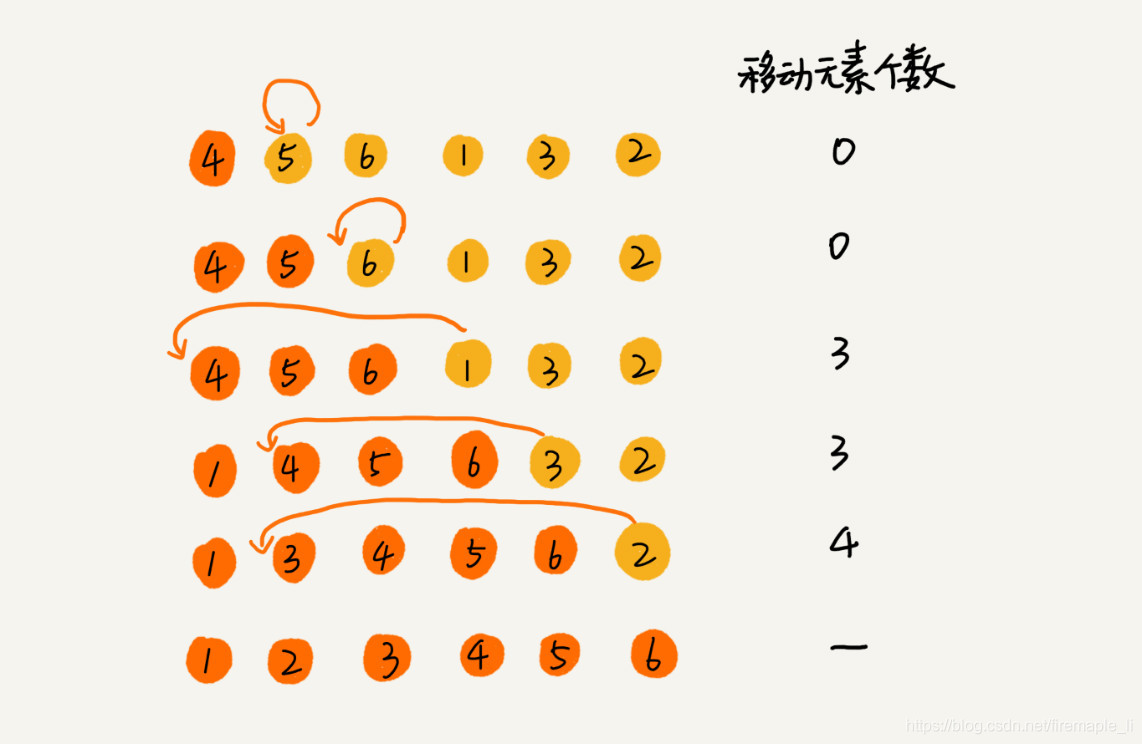
首先，我们将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序。重复这个过程，直到未排序区间中元素为空，算法结束

在这里插入图片描述

3.2代码

package com.desmond.codebase.algorithm.sorting;

import static com.desmond.codebase.algorithm.sorting.Sort.print;

/**
 * @author presleyli
 * @date 2019/1/12 5:04 PM
 */
public class InsertionSort {
    public static void main(String[] args) {
        Integer[] arr = {5,3,7,1,3,2,6,4};

        insertionSort(arr);
    }

    /**
     * 最好：已经排好序,O(n)
     * 最坏：1+2+3+...+(n-1) = n*(n-1)/2 -> O(n²)
     * 平均: ( 0 + n*(n-1)/2 ) = n*(n-1)/4 -> O(n²)
     *
     * 空间：原地排序
     * 稳定性：稳定
     * @param arr
     */
    public static void insertionSort(Integer[] arr) {
        for(int i=1; i<arr.length; i++) {
            int tmp = arr[i];

            int j = i - 1;
            for(; j >=0; j--) {
                if(tmp < arr[j]) {
                    arr[j+1] = arr[j];
                } else {
                    break;
                }
            }

            arr[j+1] = tmp;
        }

//        print(arr);
    }
}

3.3复杂度分析

3.3.1 空间

​ 原地排序

3.3.2 稳定度

​ 稳定

3.3.3 时间

  • 最好：已经排好序,O(n)

  • 最坏：1+2+3+…+(n-1) = n*(n-1)/2 -> O(n²)

  • 平均: ( 0 + n*(n-1)/2 ) = n*(n-1)/4 -> O(n²)

4. 选择排序

4.1思路

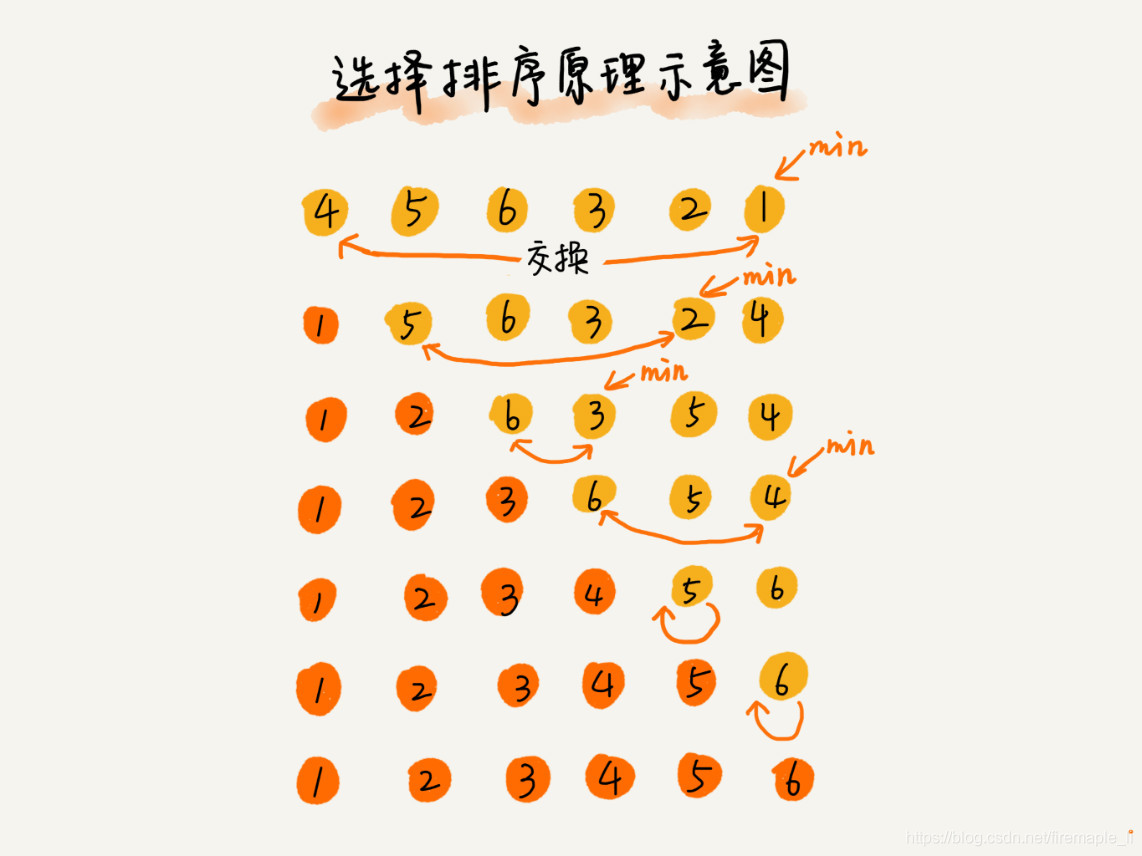
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾

在这里插入图片描述

4.2代码

package com.desmond.codebase.algorithm.sorting;

import static com.desmond.codebase.algorithm.sorting.Sort.print;

/**
 * 选择排序.
 * @author presleyli
 * @date 2019/1/12 5:04 PM
 */
public class SelectionSort {
    public static void main(String[] args) {
        Integer[] arr = {5,3,7,1,3,2,6,4};

        selectionSort(arr);

        print(arr);
    }

    /**
     * 空间：原地排序
     * 稳定度：剩下无序数组的第一个会与最小元素进行交换，不稳定。
     * 时间：
     *   最好：已经有序, 每个元素都得比较 n*n -> O(n²)
     *   最坏：完全倒序, 每个元素都得比较 n*n -> O(n²)
     *   平均：每个元素都得比较 n*n -> O(n²)
     *
     * @param arr
     */
    public static void selectionSort(Integer[] arr) {
        for(int i=0; i < arr.length; i++) {
            int j = i;
            int minIdx = j;
            for(; j < arr.length; j++) {
                if(arr[j] < arr[minIdx]) {
                    minIdx = j;
                }
            }

            // 把最小的与未排序的第一个元素进行交换
            int tmp = arr[i];
            arr[i] = arr[minIdx];
            arr[minIdx] = tmp;
        }
    }
}

4.3复杂度分析

4.3.1 空间

​ 原地排序

4.3.2 稳定度

​ 剩下无序数组的第一个会与最小元素进行交换，不稳定。

4.3.3 时间

  • 最好：已经有序, 每个元素都得比较 n*n -> O(n²)

  • 最坏：完全倒序, 每个元素都得比较 n*n -> O(n²)

  • 平均：每个元素都得比较 n*n -> O(n²)

5. 几种算法比较

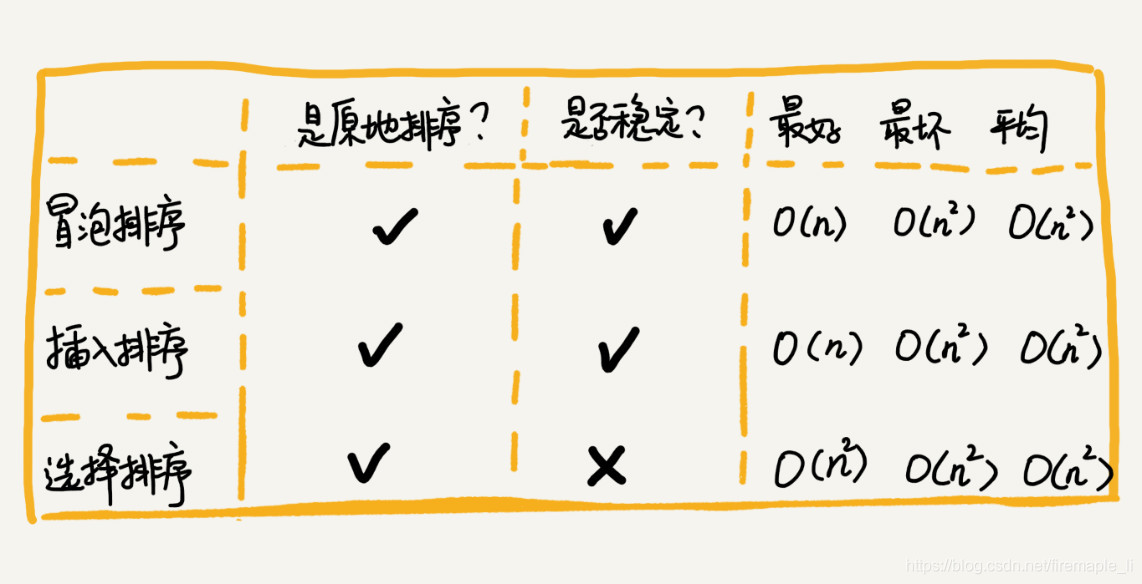
在这里插入图片描述

插入排序与冒泡排序复杂度都一样，但是插入优于冒泡，原因如下：

// 冒泡三次赋值：
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;

// 插入只需一次赋值
if(tmp < arr[j]) {
    arr[j+1] = arr[j];
} else {
    break;
}

对于数量大的情况，插入排序比冒泡少了2次基本的时间操作，更有优势：

package com.desmond.codebase.algorithm.sorting;

import java.util.ArrayList;
import java.util.List;
import java.util.Random;

/**
 * @author presleyli
 * @date 2019/1/13 9:31 PM
 */
public class CompareSort {
    public static void main(String[] args) {
        List<Integer[]> list = getRandomArrs(),
                list1 = new ArrayList<>(list);

        long t = System.currentTimeMillis();
        for(Integer[] arr : list) {
            BubbleSort.bubble_optimize(arr);
        }
        System.out.println(System.currentTimeMillis() - t);

        t = System.currentTimeMillis();
        for(Integer[] arr : list1) {
            InsertionSort.insertionSort(arr);
        }
        System.out.println(System.currentTimeMillis() - t);
    }

    public static List<Integer[]> getRandomArrs() {
        List<Integer[]> list = new ArrayList<>();
        for(int i=0; i<100000;i++) {
            list.add(arr(200));
        }

        return list;
    }

    public static Integer[] arr(int n) {
        Random random = new Random();
        Integer[] arr = new Integer[n];
        for(int i=0; i<n; i++) {
            arr[i] = random.nextInt(1000);
        }

        return arr;
    }
}

结果：

24506 // 冒泡(ms)
424  // 插入(ms)
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值