条件随机场

最新推荐文章于 2022-06-05 22:43:12 发布

原创最新推荐文章于 2022-06-05 22:43:12 发布 · 288 阅读

0 ·

CC 4.0 BY-SA版权

机器学习专栏收录该内容

8 篇文章

订阅专栏

条件随机场

马尔可夫过程

定义

假设一个随机过程中， $t_n$ 时刻的状态 $x_n$ 的条件发布，只与其前一状态 $x_{n-1}$ 相关，即：

$P(x_n|x_1,x_2,...,x_{n-1}) = P(x_n|x_{n-1})$

则将其称为马尔可夫过程。

在这里插入图片描述

隐马尔科夫算法

定义

隐马尔科夫算法是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，如下图所示：
在这里插入图片描述

在隐马尔科夫模型中，包含隐状态和观察状态，隐状态 $x_i$ 对于观察者而言是不可见的，而观察状态 $y_i$ 对于观察者而言是可见的。隐状态间存在转移概率，隐状态 $x_i$ 到对应的观察状态 $y_i$ 间存在输出概率。

假设

假设隐状态 $x_i$ 的状态满足马尔可夫过程，i时刻的状态 $x_i$ 的条件分布，仅与其前一个状态 $x_{i-1}$ 相关，即：

$P(x_i|x_1,x_2,...,x_{i-1}) = P(x_i|x_{i-1})$

假设观测序列中各个状态仅取决于它所对应的隐状态，即：

$P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1},...) = P(y_i|x_{i})$

存在问题

在序列标注问题中，隐状态（标注）不仅和单个观测状态相关，还和观察序列的长度、上下文等信息相关。例如词性标注问题中，一个词被标注为动词还是名词，不仅与它本身以及它前一个词的标注有关，还依赖于上下文中的其他词。

条件随机场（以线性链条件随机场为例）

定义

给定 $X=(x_1,x_2,...,x_n)$ ， $Y=(y_1,y_2,...,y_n)$ 均为线性链表示的随机变量序列，若在给随机变量序列 X 的条件下，随机变量序列 Y 的条件概率分布 $P (Y ∣ X)$ 构成条件随机场，即满足马尔可夫性：

$P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1}) = P(y_i|x,y_{i-1},y_{i+1})$

则称为 P(Y|X) 为线性链条件随机场。

通过去除了隐马尔科夫算法中的观测状态相互独立假设，使算法在计算当前隐状态 $x_i$ 时，会考虑整个观测序列，从而获得更高的表达能力，并进行全局归一化解决标注偏置问题。

在这里插入图片描述

参数化形式

$p\left(y | x\right)=\frac{1}{Z\left(x\right)} \prod_{i=1}^{n} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$

其中：

$Z (x)$ 为归一化因子，是在全局范围进行归一化，枚举了整个隐状态序列 $x_{1…n}$ 的全部可能，从而解决了局部归一化带来的标注偏置问题。

$Z(x)=\sum_{y} \exp \left(\sum_{i, k} \lambda_{x} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$

$t_k$ 为定义在边上的特征函数，转移特征，依赖于前一个和当前位置

$s_1$ 为定义在节点上的特征函数，状态特征，依赖于当前位置。

简化形式

因为条件随机场中同一特征在各个位置都有定义，所以可以对同一个特征在各个位置求和，将局部特征函数转化为一个全局特征函数，这样就可以将条件随机场写成权值向量和特征向量的内积形式，即条件随机场的简化形式。

在这里插入图片描述

基本问题

条件随机场包含概率计算问题、学习问题和预测问题三个问题。

概率计算问题：已知模型的所有参数，计算观测序列 $Y$ 出现的概率，常用方法：前向和后向算法；

学习问题：已知观测序列 $Y$ ，求解使得该观测序列概率最大的模型参数，包括隐状态序列、隐状态间的转移概率分布和从隐状态到观测状态的概率分布，常用方法：Baum-Wehch 算法；

预测问题：一直模型所有参数和观测序列 $Y$ ，计算最可能的隐状态序列 $X$ ,常用算法：维特比算法。

概率计算问题

给定条件随机场 $P (Y ∣ X)$ ，输入序列 $x$ 和输出序列 $y$ ;

计算条件概率

$P(Y_i=y_i|x), P(Y_{i-1} = y_{i-1},Y_i = y_i|x)$

计算相应的数学期望问题；

前向-后向算法

step 1 前向计算

对观测序列 $x$ 的每个位置 $i = 1, 2, . . ., n + 1$ ，定义一个 $m$ 阶矩阵（ $m$ 为标记 $Y_i$ 取值的个数）
在这里插入图片描述

学习问题

这里主要介绍一下 BFGS 算法的思路。

输入：特征函数 $f_1,f_2,...,f_n$ ：经验分布 $P~(X,Y)\widetilde{P}(X,Y)$ ；

输出：最优参数值 $w^\widehat{w}$ ，最优模型 $Pw^(y∣x)P_{\widehat{w}}(y|x)$ 。

选定初始点 w^{(0)}，取 $B_0$ 为正定对称矩阵，k = 0;
计算 $g_k = g(w^(k))$ ，若 $g_k = 0$ ，则停止计算，否则转 (3) ；
利用 $B_k p_k = -g_k$ 计算 $p_k$ ；
一维搜索：求 $λk\lambda_k$ 使得

在这里插入图片描述

设 $w(k+1)=w(k)+λk∗pkw^{(k+1)} = w^{(k)} + \lambda_k * p_k$
计算 $g_{k+1}$ = g(w^{(k+1)}),

若 $g_k = 0$ ，则停止计算；否则，利用下面公式计算 $B_{k+1}$ :

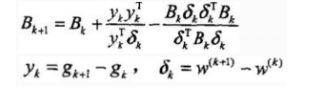
在这里插入图片描述

令 $k = k + 1$ ，转步骤（3）；

预测问题

对于预测问题，常用的方法是维特比算法，其思路如下：

输入：模型特征向量 $F (y, x)$ 和权重向量 $w$ ，输入序列（观测序列） $x={x_1,x_2,...,x_n}$ ；

输出：条件概率最大的输出序列（标记序列） $y^{*}= (y_1^*,y_2^*,...,y_n^*)$ ，也就是最优路径；
在这里插入图片描述

例子说明

利用维特比算法计算给定输入序列 $x$ 对应的最优输出序列 $y^*$ ：
在这里插入图片描述
求得最优路径 $y^{*}= (y_1^*,y_2^*,...,y_n^*) = (1,2,1)$

import numpy as np
 
class CRF(object):
    '''实现条件随机场预测问题的维特比算法
    '''
    def __init__(self, V, VW, E, EW):
        '''
        :param V:是定义在节点上的特征函数，称为状态特征
        :param VW:是V对应的权值
        :param E:是定义在边上的特征函数，称为转移特征
        :param EW:是E对应的权值
        '''
        self.V  = V  #点分布表
        self.VW = VW #点权值表
        self.E  = E  #边分布表
        self.EW = EW #边权值表
        self.D  = [] #Delta表，最大非规范化概率的局部状态路径概率
        self.P  = [] #Psi表，当前状态和最优前导状态的索引表s
        self.BP = [] #BestPath，最优路径
        return 
        
    def Viterbi(self):
        '''
        条件随机场预测问题的维特比算法，此算法一定要结合CRF参数化形式对应的状态路径图来理解，更容易理解.
        '''
        self.D = np.full(shape=(np.shape(self.V)), fill_value=.0)
        self.P = np.full(shape=(np.shape(self.V)), fill_value=.0)
        for i in range(np.shape(self.V)[0]):
            #初始化
            if 0 == i:
                self.D[i] = np.multiply(self.V[i], self.VW[i])
                self.P[i] = np.array([0, 0])
                print('self.V[%d]='%i, self.V[i], 'self.VW[%d]='%i, self.VW[i], 'self.D[%d]='%i, self.D[i])
                print('self.P:', self.P)
                pass
            #递推求解布局最优状态路径
            else:
                for y in range(np.shape(self.V)[1]): #delta[i][y=1,2...]
                    for l in range(np.shape(self.V)[1]): #V[i-1][l=1,2...]
                        delta = 0.0
                        delta += self.D[i-1, l]                      #前导状态的最优状态路径的概率
                        delta += self.E[i-1][l,y]*self.EW[i-1][l,y]  #前导状态到当前状体的转移概率
                        delta += self.V[i,y]*self.VW[i,y]            #当前状态的概率
                        print('(x%d,y=%d)-->(x%d,y=%d):%.2f + %.2f + %.2f='%(i-1, l, i, y, \
                              self.D[i-1, l], \
                              self.E[i-1][l,y]*self.EW[i-1][l,y], \
                              self.V[i,y]*self.VW[i,y]), delta)
                        if 0 == l or delta > self.D[i, y]:
                            self.D[i, y] = delta
                            self.P[i, y] = l
                    print('self.D[x%d,y=%d]=%.2f\n'%(i, y, self.D[i,y]))
        print('self.Delta:\n', self.D)
        print('self.Psi:\n', self.P)
        
        #返回，得到所有的最优前导状态
        N = np.shape(self.V)[0]
        self.BP = np.full(shape=(N,), fill_value=0.0)
        t_range = -1 * np.array(sorted(-1*np.arange(N)))
        for t in t_range:
            if N-1 == t:#得到最优状态
                self.BP[t] = np.argmax(self.D[-1])
            else: #得到最优前导状态
                self.BP[t] = self.P[t+1, int(self.BP[t+1])]
        
        #最优状态路径表现在存储的是状态的下标，我们执行存储值+1转换成示例中的状态值
        #也可以不用转换，只要你能理解，self.BP中存储的0是状态1就可以~~~~
        self.BP += 1
        
        print('最优状态路径为：', self.BP)
        return self.BP
        
def CRF_manual():   
    S = np.array([[1,1],   #X1:S(Y1=1), S(Y1=2)
                  [1,1],   #X2:S(Y2=1), S(Y2=2)
                  [1,1]])  #X3:S(Y3=1), S(Y3=1)
    SW = np.array([[1.0, 0.5], #X1:SW(Y1=1), SW(Y1=2)
                   [0.8, 0.5], #X2:SW(Y2=1), SW(Y2=2)
                   [0.8, 0.5]])#X3:SW(Y3=1), SW(Y3=1)
    E = np.array([[[1, 1],  #Edge:Y1=1--->(Y2=1, Y2=2)
                   [1, 0]], #Edge:Y1=2--->(Y2=1, Y2=2)
                  [[0, 1],  #Edge:Y2=1--->(Y3=1, Y3=2) 
                   [1, 1]]])#Edge:Y2=2--->(Y3=1, Y3=2)
    EW= np.array([[[0.6, 1],  #EdgeW:Y1=1--->(Y2=1, Y2=2)
                   [1, 0.0]], #EdgeW:Y1=2--->(Y2=1, Y2=2)
                  [[0.0, 1],  #EdgeW:Y2=1--->(Y3=1, Y3=2)
                   [1, 0.2]]])#EdgeW:Y2=2--->(Y3=1, Y3=2)
    
    crf = CRF(S, SW, E, EW)
    ret = crf.Viterbi()
    print('最优状态路径为:', ret)
    return
    
if __name__=='__main__':
    CRF_manual()