汇编语言实验10(2) 入门级视野

最新推荐文章于 2021-10-16 14:28:06 发布

原创最新推荐文章于 2021-10-16 14:28:06 发布 · 217 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#王爽汇编 ms-dos

汇编语言学习专栏收录该内容

3 篇文章

订阅专栏

本文深入探讨了32位除法中溢出问题的解决方案，通过将被除数分为高低两部分，利用十六进制特性进行精确计算，避免了传统方法中的溢出风险。文中详细解释了如何通过调整算法实现更高效的除法运算，同时提供了具体的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

(2)解决除法溢出的问题
问题的精髓在于理解

X / N = int(H / N) * 65536 + [rem( H / N) * 65536 + L] / N

在这里插入图片描述
H / N 有什么特点？最大的特点就是它的余数不能被N整除。这有什么意义？我们来看看除法的过程。

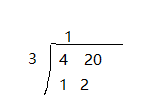
大家思考一下这个简单的除法，1位高位，20位低位。H / N想要继续除法，必须要借位对吧。也就是说(H % N) * 10 + 20 除以3的结果肯定是两位数可以容纳的。同理，对于十六进制呢？我们可以将32位的被除数，分成上图中的高、低16位。那么便有

X / N = H / N * 65536 + ((H % N) * 65536 + L) / N 
X % N = ((H % N) * 65536 + L) % N

那么除法的商为32位

AX = ((H % N) * 65536 + L) / N 
DX = H / N

余数

CX = ((H % N) * 65536 + L) % N

最终代码：

assume cs:code

code segment
	start:
	mov ax,4240h
	mov dx,000fh
	mov cx,0ah
	call divdw
	mov ax,4c00h
	int 21h

	divdw:
		push ax		;需要先计算H / N
		mov ax,dx	
		mov dx,0	;将高位置为0
		div cx		;计算H / N, 此时ax存放H / N（高16位商）, dx存放 H % N（高16位余数）
		mov bx,ax 	;保存 H / N（商）

		pop ax
		div cx		;此时 ax为低16值, dx为高16的商 ,那么就是计算((H % N) * 65536 + L) / N 
		;计算完成之后将商保存在ax,余数存放在dx
		mov cx,dx 	;将dx的余数转存cx
		mov dx,bx 	;将bx中的高16位商存到dx
		ret
code ends
end start