堆排序--Java

定义

堆排序是一种树形选择排序方法，特点：排序过程中，将nums[1...n]看成一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序区中选择最大（最小）元素。

堆的定义如下：n个关键字序列满足如下关系：

• nums[i] <= nums[2i] 且 nums[i] <= nums[2i + 1]     (小根堆）
• nums[i] >= nums[2i] 且 nums[i] >= nums[2i + 1]   （大根堆）

堆排序

堆排序的关键是构造初始堆，其中最核心的是向下调整。

n个结点的完全二叉树，最后一个结点是⌊n/2⌋个结点的孩子。对第⌊n/2⌋个结点为根结点的子树筛选（对于大根堆，若根结点小于左右孩子结点较大者，则交换，否则不交换），使该子树成为堆。之后向前对各结点（⌊n/2⌋ - 1 ~ 1）为根的子树进行筛选，看该根结点是否大于左右孩子结点，如果小于孩子结点，则交换，交换之后可能破坏下一级的堆，继续用该方法向下调整，确保下一级也为堆，直至最后叶子节点或者不用调整也为堆停止。反复利用上诉方法，直至第一个结点。

• 
• 
• 
• 
• 
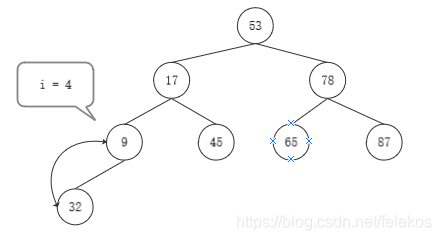
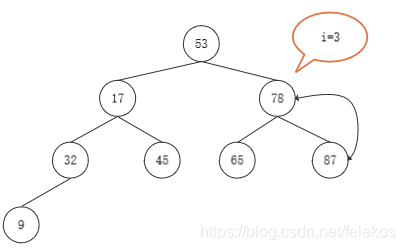
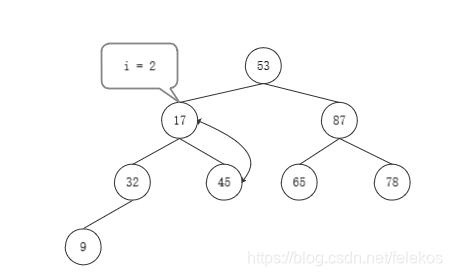
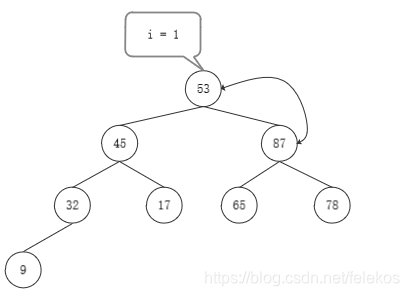
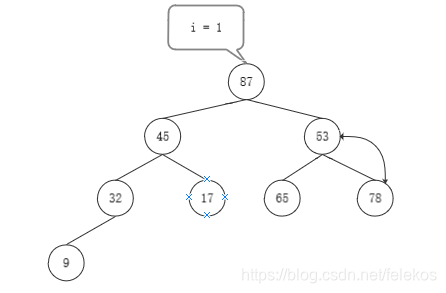
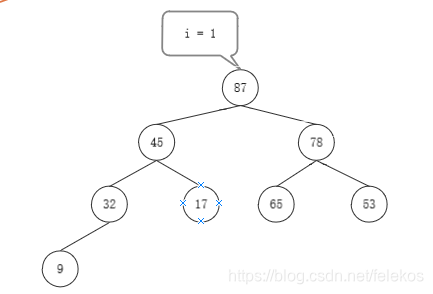
• 结果
• 

附录代码

public class HeapSort {

    String name;
    int id;

    public HeapSort(String name, int id){
        this.name = name;
        this.id = id;
        System.out.println("hello");
    }

    public void sort(int[] nums){
        buildMaxHeap(nums);
        for(int i = nums.length; i > 1; i--){
            int temp = nums[0];
            nums[0] = nums[i - 1];
            nums[i - 1] = temp;
            adjustDown(nums, 1, i - 1);
        }
    }

    public void buildMaxHeap(int[] nums){
        for(int i = nums.length / 2; i > 0; i--) // [0 2 3 4 ...], i,若数组索引以1开始 其左孩子为2i，右孩子为2i + 1
        {
           adjustDown(nums, i, nums.length);
        }
    }

    // 注意访问的时候-1.
    public void adjustDown(int[] nums, int pos, int size){
        int temp = nums[pos - 1];
        for(int i = 2 * pos; i <= size; i *= 2)
        {
            if(i < size && nums[i - 1] < nums[i]){ // 如果有右孩子，且右孩子更大,-1
                i++;
            }
            if(temp >= nums[i - 1])
                break;
            else{
                nums[pos - 1] = nums[i - 1];
                pos = i;
            }
        }
        nums[pos - 1] = temp;
    }

    public static void main(String[] args){
        int[] nums = {53, 17, 78, 9, 45, 65, 87, 32};
        HeapSort newObj = new HeapSort("我是堆排序", 18);
        newObj.sort(nums);
        for(int i = 0; i < nums.length; i++)
            System.out.println(nums[i]);
    }
}