直流亥姆霍兹线圈和交流亥姆霍兹线圈的区别

亥姆霍兹线圈（Helmholtz coil）是一种制造小范围区域均匀磁场的器件。由于亥姆霍兹线圈具有开敞性质，很容易地可以将其它仪器置入或移出，也可以直接做视觉观察，所以，是物理实验常使用的器件。因德国物理学者赫尔曼·冯·亥姆霍兹而命名。

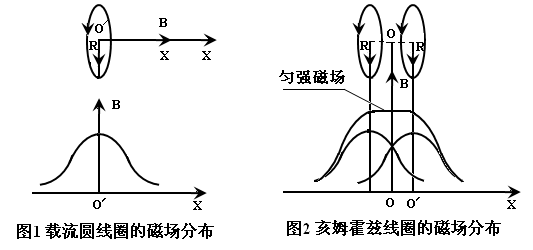
亥姆霍兹线圈是一对彼此平行且连通的共轴圆形线圈,两线圈内的电流 方向一致,大小相同,线圈之间的距离 d 正好等于圆形线圈的半径 R 时，这种圆形载流线圈称为Helmhohz线圈,。这种线圈的特点是能在其公共轴线中点附近产生较广的均匀磁场。

直流亥姆霍兹线圈和交流亥姆霍兹线圈的区别
　　亥姆霍兹线圈是由两个单线圈组成，典型应用为测量磁场（磁生电）和发生磁场（电生磁）在发生磁场时，两线圈轴距中心点产生均匀磁场具有均匀区体积大，使用空间开阔等特点。实现一维、二维、三维组合磁场，可提供交、直流磁场，电流与磁场有很好的线性关系。适用于各研究所，高等院校及企业做物质磁性或检测实验，应用于材料、电子、生物、医疗等.当亥姆霍兹线圈供电电源为直流恒流电源，那么产生的磁场为直流磁场，反之当供电电源为交流电源产生的磁场就是交流磁场。
　　湖南省永逸科技有限公司亥姆霍兹线圈案例图片分享

一维亥姆霍兹线圈

三维亥姆霍兹线圈案例图片

亥姆霍兹线圈

亥姆霍兹线圈系统

一维亥姆霍兹线圈

一维亥姆霍兹线圈