网格处理:Laplace
参考:
https://blog.youkuaiyun.com/hjimce/article/details/46505863
https://blog.youkuaiyun.com/hjimce/article/details/46415239
laplace算子在网格平滑,remesh,网格编辑中都有应用。它全局线性的特点。
什么是laplace算子
参考:https://blog.youkuaiyun.com/hjimce/article/details/46415239
laplace算子是梯度的散度
在离散的情况下:
laplace算子的计算如下:

由于
∑wij=1 \sum w_{ij} = 1 ∑wij=1
vi=∑wij∗vi v_i = \sum w_{ij}*vi vi=∑wij∗vi
L(vi)=∑wij(vi−vj) L(v_i) = \sum w_{ij}(v_i-v_j) L(vi)=∑wij(vi−vj)
laplace算子的几何意义
了解了laplace算子的计算公式,可以得到laplace算子的几何意义:
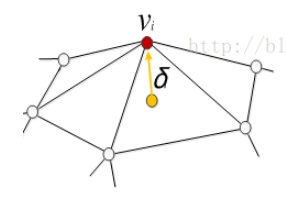
即:δ\deltaδ是viv_ivi到周围所有vjv_jvj根据权重wijw_{ij}wij计算得到的vi′v_i'vi′的向量。
这个向量δ\deltaδ被称为viv_ivi的微分坐标了,计算微分坐标的意义在于,Laplace形变认为这个微分坐标能够记录或者说表示模型的局部细节信息,比如鼻子,嘴巴,凸起,凹陷这样的信息,当模型形变后,我们希望模型的局部信息不要被破坏,那么换成坐标的说法就是,模型上点的世界坐标变了,但是我们希望模型上所有点的微分坐标没变,也就是点和点的相对位置关系没变。
laplace算子-网格平顺
论文:Laplacian Mesh Optimization


当网格曲面上任意顶点的局部片中包含的所有三角面片都为等腰三角形时,该顶点的同一Laplacian 坐标和余切Laplacian 坐标相等。当将上述结论由某一个三角面片扩展到整个模型表面时可以发现:如果所有的三角面片都接近于正三角形,所有顶点的同一(均匀)Laplacian 坐标和余切Laplacian 坐标接近相等。
算法原理主要是:
1、通过先求解网格曲面余切权计算得到的Laplacian 坐标δ
2、构建均匀权下的拉普拉斯矩阵A
3、然后求解AX=δ.
laplace算子-网格去噪
均匀权下的拉普拉斯就是网格平滑
laplace算子-网格编辑
论文:Laplacian mesh optimization
参考
https://blog.youkuaiyun.com/bob__yuan/article/details/81778875





 本文详细介绍了Laplace算子的概念及其在网格平滑、去噪及编辑中的应用。通过数学公式解析laplace算子的计算方式,并阐述其几何意义,即能够记录模型的局部细节信息。此外,还探讨了Laplacian坐标在网格优化和平滑中的作用。
本文详细介绍了Laplace算子的概念及其在网格平滑、去噪及编辑中的应用。通过数学公式解析laplace算子的计算方式,并阐述其几何意义,即能够记录模型的局部细节信息。此外,还探讨了Laplacian坐标在网格优化和平滑中的作用。
















 944
944

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








