吴恩达471机器学习入门课程2第3周——评估和改进模型

探索评估和改进机器学习模型的技术。

1 导包

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.activations import relu,linear
from keras.losses import SparseCategoricalCrossentropy
from keras.optimizers import Adam
import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)

from public_tests_a1 import *

tf.keras.backend.set_floatx('float64')
from assigment_utils import *

tf.autograph.set_verbosity(0)

2 - 评估学习算法（多项式回归）

假设你已经创建了一个机器学习模型，并且发现它非常适合你的训练数据。完成了吗？不完全是。创建模型的目标是能够预测新示例的值。

在部署模型之前，如何测试您的模型在新数据上的表现呢？
答案有两个部分：

• 将原始数据集拆分为“训练”和“测试”集。
  • 使用训练数据来拟合模型参数
  • 使用测试数据来评估模型在新数据上的表现
• 开发一个误差函数来评估您的模型。

2.1 划分数据集

'''
这是一个 Python 函数，用于生成一个基于的X²数据集，并添加噪声。函数的输入参数为 m、seed 和 scale，其中 m 是数据点的数量，seed 是随机种子，scale 是噪声的大小。函数会输出四个变量 x_train、y_train、x_ideal 和 y_ideal。

具体地说，函数首先将 0 到 49 均匀分成 m 段，并生成一个长度为 m 的数组 x_train，该数组包含了用于拟合数据的 x 值。接下来，函数使用给定的随机种子生成一组随机数，并根据这些随机数生成一个长度为 m 的噪声数组，将其加到中X²，得到理想的 y 值 y_ideal。然后，函数在 y_ideal 上加上一定比例的噪声，得到最终的可训练数据 y_train。同时，函数还将 x_train 和 y_ideal 输出，以便在需要时重新绘制数据。
'''
'''
在数据分析和机器学习中，噪声通常指的是数据中不希望出现的随机误差或干扰。这些误差可能来自于测量设备的精度限制、信号传输过程中的干扰、数据采集时的环境噪声等各种因素。

在这个函数中，为了模拟真实数据中的噪声，我们使用了一组随机数并将其加到理想的X²函数值上，得到了最终的可训练数据 y_train。这样做的目的是为了使生成的数据更接近真实场景，并且能够更好地验证模型的鲁棒性和泛化能力。
'''
def gen_data(m, seed=1, scale=0.7):
    """ generate a data set based on a x^2 with added noise """
    c = 0
    x_train = np.linspace(0,49,m)
    np.random.seed(seed)
    y_ideal = x_train**2 + c
    y_train = y_ideal + scale * y_ideal*(np.random.sample((m,))-0.5)
    x_ideal = x_train #for redraw when new data included in X
    return x_train, y_train, x_ideal, y_ideal

X,y,x_ideal,y_ideal = gen_data(18, 2, 0.7)
print("X.shape", X.shape, "y.shape", y.shape)
'''
这段代码用于从数据集中划分出训练集和测试集。其中，X表示特征变量的数据集，y表示目标变量的数据集，test_size=0.33表示将数据集按3:1的比例划分为训练集和测试集，
random_state=1是为了确定随机种子，保证每次划分的结果都一样。
具体来说，该函数会将X和y分别划分为X_train、X_test和y_train、y_test四个数据集，其中X_train和y_train用于训练模型，X_test和y_test用于评估模型的性能。
'''
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33, random_state=1)
print("X_train.shape", X_train.shape, "y_train.shape", y_train.shape)
print("X_test.shape", X_test.shape, "y_test.shape", y_test.shape)

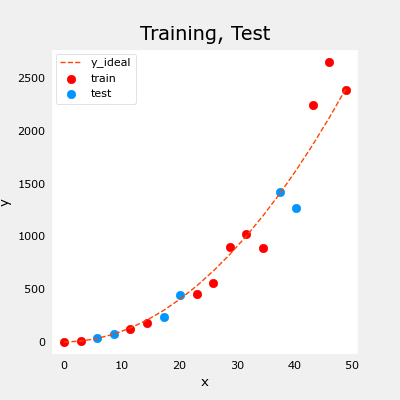
2.1.1 绘制训练集和测试集

您可以看到，下面的数据点将作为训练的一部分（红色）与模型未经过训练的数据（测试）混合在一起。这个特定的数据集是一个带有噪声的二次函数。参考曲线显示出“理想”的曲线。

fig, ax = plt.subplots(1,1,figsize=(4,4))
ax.plot(x_ideal, y_ideal, "--", color = "orangered", label="y_ideal", lw=1)
ax.set_title("Training, Test",fontsize = 14)
ax.set_xlabel("x")
ax.set_ylabel("y")

ax.scatter(X_train, y_train, color = "red",           label="train")
ax.scatter(X_test, y_test,   color = dlc["dlblue"],   label="test")
ax.legend(loc='upper left')
plt.show()

Figure

2.2 模型评估的误差计算，线性回归

当评估线性回归模型时，您需要对预测值和目标值之间的平方误差差异进行平均。公式如下：
$$J_{\text{test}}(\mathbf{w},b)=\frac{1}{2m_{\text{test}}}\sum _{i=0}^{m_{\text{test}}-1}(f_{\mathbf{w},b}({\mathbf{x}}_{\text{test}}^{(i)})-y_{\text{test}}^{(i)}{)}^2\text{\hspace{1em}(1)}$$

# 均方差
def eval_mse(y,yhat):
     m = len(y)
     err = 0.0
     for i in range(m):
         err+=np.power(y[i]-yhat[i],2)
     err/=2*m
     return err

2.3 比较训练数据和测试数据上的性能

让我们构建一个高阶多项式模型以最小化训练误差。这将使用sklearn中的linear_regression函数。如果您想查看详细信息，请查看导入的实用程序文件中的代码。以下是步骤：

• 创建并拟合模型（‘fit’ 是另一个训练或运行梯度下降的名称）。
• 计算训练数据上的误差。
• 计算测试数据上的误差。

num = 10
lmodel = lin_model(num)
lmodel.fit(X_train,y_train)

yhat = lmodel.predict(X_train)
err_train = lmodel.mse(y_train, yhat)

yhat = lmodel.predict(X_test)
err_test = lmodel.mse(y_test,yhat)

训练集上的计算误差远远小于测试集的计算误差。

print(f"training err {
     
     err_train:0.2f}, test err {
     
     err_test:0.2f}")

training err 58.01, test err 171215.01

以下的图表展示了为什么会这样。该模型非常精确地拟合了训练数据，但为此它创建了一个复杂的函数。测试数据不是训练数据的一部分，所以该模型在这些数据上的预测效果很差。
因此，这个模型可以被描述为：1）过度拟合，2）方差高，3）泛化能力差。

x = np.linspace(0,int(X.max()),100)  # predict values for plot
y_pred = lmodel.predict(x).reshape(-1,1)

plt_train_test(X_train, y_train, X_test, y_test, x, y_pred, x_ideal, y_ideal, num)

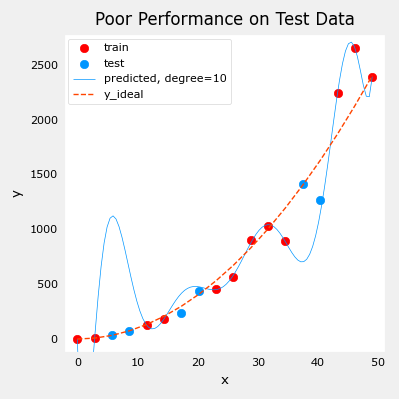
以下的测试数据误差表明该模型在新数据上效果不佳。如果将测试误差用于指导改进模型，则该模型会在测试数据上表现良好……但是，测试数据旨在代表新的数据。

你需要另一个数据集来测试新数据的表现。

讲座期间提出的建议是将数据分成三组。下表所示的训练、交叉验证和测试集的分布是典型的分布，但可以根据可用数据量进行变化。

数据集	总数的百分比	描述
训练集	60	用于调整模型参数 $w$ 和 $b$ 的数据，即用于训练或拟合的数据
交叉验证集	20	用于调整其他模型参数，如多项式的次数、正则化或神经网络的架构。
测试集	20	用于在调整后测试模型，以衡量在新数据上的性能

让我们生成三个数据集。我们将再次使用sklearn中的train_test_split，但要调用两次以获取三个拆分：

X,y, x_ideal,y_ideal = gen_data(40, 5, 0.7)
print("X.shape", X.shape, "y.shape", y.shape)
X_train, X_, y_train, y_ = train_test_split(X,y,test_size=0.40, random_state=1)
X_cv, X_test, y_cv, y_test = train_test_split(X_,y_,test_size=0.50, random_state=1)
print("X_train.shape", X_train.shape, "y_train.shape", y_train.shape)
print("X_cv.shape", X_cv.shape, "y_cv.shape", y_cv.shape)
print("X_test.shape", X_test.shape, "y_test.shape", y_test.shape)

X.shape (40,) y.shape (40,)
X_train.shape (24,) y_train.shape (24,)
X_cv.shape (8,) y_cv.shape (8,)
X_test.shape (8,) y_test.shape (8,)

3 偏差和方差

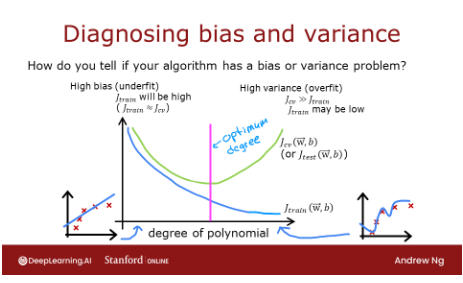
以上，很明显多项式模型的次数太高了。你如何选择一个好的值？事实证明，正如图表所示，训练和交叉验证的表现可以提供指导。通过尝试一系列次数值，可以评估训练和交叉验证的表现。随着次数变得过大，交叉验证表现将开始相对于训练表现而降低。我们在例子中试一试这个方法。

3.1 绘制训练、交叉验证和测试集

您可以在下面看到将成为训练数据点的数据（以红色表示）与模型未经过训练的数据（测试集和交叉验证集）混合在一起的情况。

fig, ax = plt.subplots(1,1,figsize=(4,4))
ax.plot(x_ideal, y_ideal, "--", color