二叉查找树

二叉查找树

每个节点最多只有两个子树的树结构，通常子树被称为左子树或者右子树，二叉查找树的重要性质是：对于树中的每个节点x，左子树任意节点的值都小于X ，右子树任意节点的值均大于X。注意：索引的存储块和之前说的数据库最小存储单位块或者页实际上并非一一对应，只是为了方便我们的理解将其一一对应起来。索引的每个存储块存储的是关键字+指向子树的指针，像下图中的树，不仅仅是二叉树还是平衡二叉树。

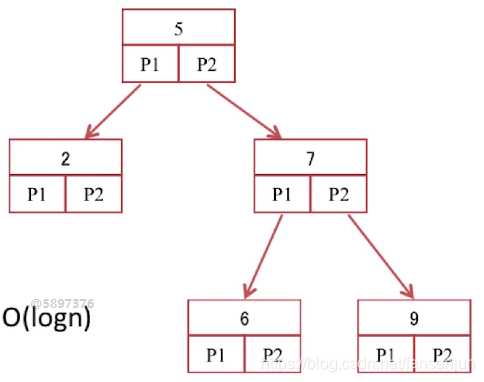
什么是平衡二叉树：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。查找元素的时候使用二分查找，所以查找的速度很快，不过还是有缺点的：首先我们的数据库会面临数据的增加或者删除。

B-Tree

又叫做平衡多路查找树，如果每个节点最多有m个孩子，那么这样的树就叫做m阶B-Tree树，如下图就是一个3阶B树，每个存储块中都包含了关键字和指向孩子的指针，最多有几个孩子取决于存储块的容量以及数据库的相关配置，所以通常情况下这个m是很大的

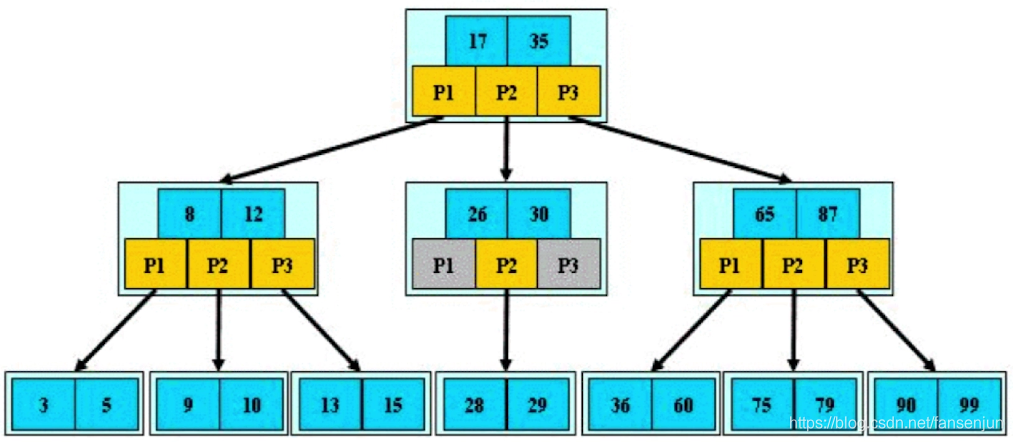
定义：

• 根节点至少包括两个孩子
• 树中的每个节点最多含有m个孩子（m>=2）
• 除根节点和叶节点外，其他每个节点至少有ceil（m/2）个孩子
• 所有叶子结点都位于同一层

最后一个约束如下：

B+-Tree

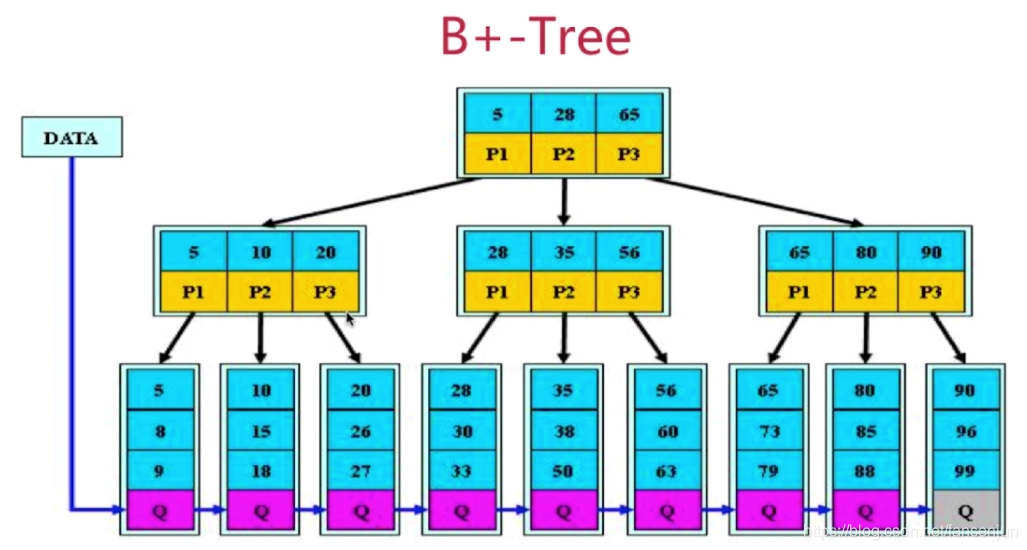
B+树是B树的变体，其定义基本与B树相同，除了：

• 非叶子节点的子树指针与关键字个数相同
• 非叶子节点的子树指针P[i]，指向关键字值[k[i],k[i-1]）的子树
• 非叶子节点仅用来做索引，数据都保留在叶子节点中
• 所有的叶子节点均有一个链指针指向下一个叶子节点

结论

B+-Tree更适合用来做存储索引

• B+-Tree的磁盘读写代价更低

B+-Tree的内部结构，并没有指向关键字的具体信息指针，也就是说不存放数据，只存放索引信息，因此其内部节点相对于B-Tree来说更小，如果把所有同一内部关键字存放在同一盘块中，这个盘块所能容纳的关键字数量也越多，一次性读入到内存中的需要查找的关键字也就越多，相对来说IO读写次数也就降低了

• B+-Tree树的查询效率稳定

由于内部节点并不是最终指向文件内容的节点，而只是叶子节点中关键字的索引，所以任何关键字的查找必须走一条从根节点到叶子节点的路，所有关键字查询的长度相同，导致每一个数据查询效率也几乎是相同的，稳定的复杂度

• B+-Tree更有利于对数据库的扫描

B+树只需要遍历叶子节点就可以解决对全部关键字的扫描，所以对数据库中频繁的使用范围查询