Description
Plato believed what we perceive is but a shadow of reality. Recent archaeological excavations have uncovered evidence that this belief may have been encouraged by Plato's youthful amusement with cleverly-designed blocks. The blocks
have the curious property that, when held with any face toward a light source, they cast shadows of various letters, numbers, shapes, and patterns. It is possible for three faces incident to a corner to correspond to three different shadow patterns. Opposite
faces, of course, cast shadows which are mirror images of one another.
The blocks are formed by gluing together small cubes to form a single, connected object. As an example, the figures below show, layer by layer, the internal structure of a block which can cast shadows of the letters "E", "G", or "B".
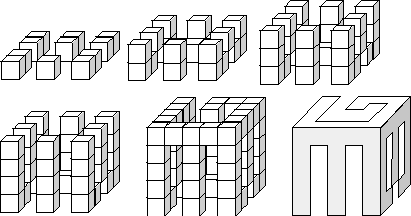
Only a partial set of blocks was discovered, but the curious scientists would like to determine what combinations of shadows are possible. Your program, the solution to this problem, will help them! The program will input groups of shadow patterns, and for each group will report whether or not a solid can be constructed that will cast those three shadows.
The blocks are formed by gluing together small cubes to form a single, connected object. As an example, the figures below show, layer by layer, the internal structure of a block which can cast shadows of the letters "E", "G", or "B".

Only a partial set of blocks was discovered, but the curious scientists would like to determine what combinations of shadows are possible. Your program, the solution to this problem, will help them! The program will input groups of shadow patterns, and for each group will report whether or not a solid can be constructed that will cast those three shadows.
Input
The input contains a sequence of data sets, each specifying a dimension and three shadow patterns. The first line of a data set contains a positive integer 1 <= n <= 20 that specifies the dimensions of the input patterns. The remainder
of the data set consists of 3n lines, each containing a string of n "X" and "-" characters. Each group of n lines represents a pattern. Where an "X" appears a shadow should be cast by the final solid, and where a "-" appears, light should pass through. For
this problem, the input patterns may be assumed to have at least one "X" along each edge of the pattern. The input is terminated by a line containing a single zero in place of a valid dimension.
Output
For each data set in the input, output the data set number and one of the following messages:
Valid set of patterns
Impossible combination
For a set of patterns to be considered valid, it must be possible to construct, by gluing unit cubes together along their faces, a one-piece solid capable of casting the shadow of each of the input patterns.
Valid set of patterns
Impossible combination
For a set of patterns to be considered valid, it must be possible to construct, by gluing unit cubes together along their faces, a one-piece solid capable of casting the shadow of each of the input patterns.
Sample Input
5 XXXXX X---- X--XX X---X XXXXX XXXXX X---- XXXXX X---- XXXXX XXXXX X---X XXXX- X---X XXXXX 3 X-- -X- --X XX- XXX -XX -XX XXX XX- 0
Sample Output
Data set 1: Valid set of patterns Data set 2: Impossible combination
思路:把给出的三个面当三视图,判断它能否组成一个物体。坑点在于给出的每个面都有8种可能情况:旋转,翻转,翻转之后再旋转。
#include <stdio.h>
bool a[20][20][20],vis[20][20][20];
char b[8][20][21],c[8][20][21],d[8][20][21];
int n;
void search(int x,int y,int z)
{
vis[x][y][z]=1;
if(x+1<n && !vis[x+1][y][z] && a[x+1][y][z]) search(x+1,y,z);
if(y+1<n && !vis[x][y+1][z] && a[x][y+1][z]) search(x,y+1,z);
if(z+1<n && !vis[x][y][z+1] && a[x][y][z+1]) search(x,y,z+1);
if(x-1>=0 && !vis[x-1][y][z] && a[x-1][y][z]) search(x-1,y,z);
if(y-1>=0 && !vis[x][y-1][z] && a[x][y-1][z]) search(x,y-1,z);
if(z-1>=0 && !vis[x][y][z-1] && a[x][y][z-1]) search(x,y,z-1);
}
int main()
{
int i,j,k,flag,ok,cnt=1,count,o,p,q;
while(scanf("%d",&n) && n)
{
for(i=0;i<n;i++) scanf("%s",b[0][i]);
for(i=0;i<n;i++) scanf("%s",c[0][i]);
for(i=0;i<n;i++) scanf("%s",d[0][i]);
for(k=1;k<=3;k++)//考虑各个面的不同情况
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
b[k][i][j]=b[k-1][j][n-1-i];
c[k][i][j]=c[k-1][j][n-1-i];
d[k][i][j]=d[k-1][j][n-1-i];
}
}
}
for(k=4;k<=4;k++)//考虑各个面的不同情况
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
b[4][i][j]=b[0][n-1-i][n-1-j];
c[4][i][j]=c[0][n-1-i][n-1-j];
d[4][i][j]=d[0][n-1-i][n-1-j];
}
}
}
for(k=5;k<=7;k++)//考虑各个面的不同情况
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
b[k][i][j]=b[k-1][j][n-1-i];
c[k][i][j]=c[k-1][j][n-1-i];
d[k][i][j]=d[k-1][j][n-1-i];
}
}
}
ok=0;
for(o=0;o<8 && !ok;o++) for(p=0;p<8 && !ok;p++) for(q=0;q<8 && !ok;q++)
{
for(i=0;i<n;i++) for(j=0;j<n;j++) for(k=0;k<n;k++) a[i][j][k]=vis[i][j][k]=0;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
for(k=0;k<n;k++)
{
if(b[o][i][j]=='X' && c[p][j][k]=='X' && d[q][i][k]=='X') a[i][j][k]=1;
}
}
}
ok=1;
for(i=0;i<n && ok;i++)
{
for(j=0;j<n && ok;j++)
{
if(b[o][i][j]=='X')
{
flag=0;
for(k=0;k<n && ok;k++)
{
if(a[i][j][k])
{
flag=1;
break;
}
}
if(!flag)
{
ok=0;
break;
}
}
}
}
for(j=0;j<n && ok;j++)
{
for(k=0;k<n && ok;k++)
{
if(c[p][j][k]=='X')
{
flag=0;
for(i=0;i<n && ok;i++)
{
if(a[i][j][k])
{
flag=1;
break;
}
}
if(!flag)
{
ok=0;
break;
}
}
}
}
for(i=0;i<n && ok;i++)
{
for(k=0;k<n && ok;k++)
{
if(d[q][i][k]=='X')
{
flag=0;
for(j=0;j<n && ok;j++)
{
if(a[i][j][k])
{
flag=1;
break;
}
}
if(!flag)
{
ok=0;
break;
}
}
}
}
count=0;
for(i=0;i<n && ok;i++)
{
for(j=0;j<n && ok;j++)
{
for(k=0;k<n && ok;k++)
{
if(a[i][j][k] && !vis[i][j][k])
{
count++;
search(i,j,k);
}
}
}
}
if(count!=1) ok=0;
if(ok)
{
printf("Data set %d: Valid set of patterns\n",cnt++);
break;
}
}
if(!ok) printf("Data set %d: Impossible combination\n",cnt++);
}
}





 本文深入探讨了游戏开发领域中技术美术的关键角色,从游戏引擎的选择、动画制作到UV贴图处理等,全面解析了技术美术如何在游戏开发过程中发挥重要作用,提升游戏品质。
本文深入探讨了游戏开发领域中技术美术的关键角色,从游戏引擎的选择、动画制作到UV贴图处理等,全面解析了技术美术如何在游戏开发过程中发挥重要作用,提升游戏品质。
















 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








