AirSim高保真自动驾驶仿真

AirSim：用于自动驾驶车辆的高保真视觉与物理仿真

1 引言

最近，强化学习[1],示范学习[2]和迁移学习[3]等范式被证明是训练各种机器人系统的自然方法。使用这些技术的一个关键挑战是样本复杂度高——学习有用行为所需的训练数据量通常过高。此外，由于自动驾驶车辆在训练阶段往往存在安全风险且操作成本高昂，这一问题进一步加剧。为了在现实世界中无缝运行，机器人需要将在仿真中获得的学习成果进行迁移。目前，这是一项非平凡的任务，因为仿真感知、环境和执行器通常过于简单，缺乏真实世界的丰富性或多样性。例如，对于旨在户外环境中使用计算机视觉的机器人而言，可能需要对真实世界中的复杂物体（如树木、道路、湖泊、电线杆和房屋）进行建模，同时渲染效果还需包含柔和阴影、镜面反射、漫反射互反射等更精细的细节。同样，开发更精确的系统动力学模型也至关重要，以使模拟行为能够紧密地模仿真实世界。

AirSim 是一个开源平台 [4]旨在缩小仿真与现实之间的差距，以支持自动驾驶车辆的开发。该平台致力于积极推动数据驱动型机器智能技术（如强化学习和深度学习）的开发与测试。它受到多个先前模拟器的启发（参见相关工作），我们的主要目标之一是建立一个社区，共同推动该领域的前沿发展。

2 相关工作

尽管全面回顾当前使用的模拟器超出了本文的范围，但我们提及了一些与我们设定最接近且对本研究产生深远影响的近期重要工作。

Gazebo [5]一直是研究工作中最受欢迎的仿真平台之一。它采用模块化设计，可支持不同的物理引擎、传感器模型，并能够创建三维世界。Gazebo超越了整体式刚体车辆的范畴，可用于模拟具有连杆与关节结构的更通用机器人，例如复杂机械臂或双足机器人。尽管Gazebo功能较为丰富，但在构建接近现实世界的大规模、视觉效果复杂的环境方面仍存在困难，且在渲染技术方面落后于虚幻引擎或Unity等平台的诸多进展。

其他值得注意的努力包括Hector [6]，其主要侧重于与流行的中间件 ROS和Gazebo的紧密集成。它提供了风洞调校的飞行动力学、包含使用高斯‐马尔可夫过程的偏置漂移的传感器模型，以及基于Orocos工具链的软件在环。然而，Hector缺乏对Pixhawk等流行硬件平台和MavLink等协议的支持。由于其对ROS和Gazebo的紧密依赖，如前所述，它受限于模拟环境的丰富性。

类似地，RotorS [7]提供了一个模块化框架，用于设计微型飞行器，并构建可在模拟器中测试的控制和状态估计算法。可以为RotorS配置支持Pixhawk的硬件在环（HITL）。RotorS也使用Gazebo作为其平台，从而限制了其与感知相关的能力。

最后，jMavSim [8]是一款易于使用的模拟器，旨在测试PX4固件和设备，因此与PX4仿真紧密集成。

API，使用了虽然较简单的传感器模型，并利用了环境中没有任何物体的简化渲染引擎。

除此之外，还有许多类似模拟器的游戏和训练应用，但这些大多是商业闭源软件，关于模型、仿真精度或自主应用的开发API方面，公开信息很少甚至没有。

3 架构

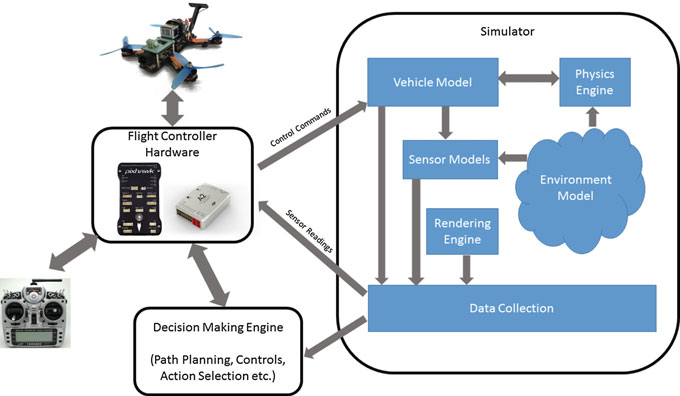
我们的模拟器采用模块化设计，注重可扩展性。核心组件包括环境模型、车辆模型、物理引擎、传感器模型、渲染接口、公共API层以及用于车辆固件的接口层，如图2所示。

典型的自主空中飞行器系统包括飞控固件，例如 PX4[9],ROSFlight [10], Hackflight [11]等。飞控控制器以期望状态和传感器数据作为输入，计算当前状态的估计值，并输出执行器控制信号以实现期望状态。例如，在四旋翼飞行器的情况下，用户可将期望的俯仰角、横滚角和偏航角作为期望状态，飞控控制器则可利用来自加速度计和陀螺仪的传感器数据来估计当前角度，最终计算出实现期望角度所需的电机信号。

在仿真过程中，模拟器将来自模拟世界的传感器数据提供给飞控控制器。飞控控制器输出执行器信号，这些信号由模拟器的车辆模型组件接收作为输入。车辆模型的目标是计算由模拟执行器产生的力和扭矩。例如，在四旋翼飞行器的情况下，根据电机电压计算螺旋桨产生的推力和扭矩。此外，还可能存在来自阻力、摩擦和重力的力。这些力和扭矩随后被物理引擎接收，用于计算模拟世界中物体的下一个运动学状态。该物体的运动学状态以及重力、空气密度、气压、磁场和地理位置 （GPS坐标）的环境模型共同为模拟传感器模型提供真实值。

飞控控制器的期望状态输入可由人工操作员通过遥控器设置，或在自主模式下由机载计算机设置。机载计算机可以执行复杂的高层计算，例如确定下一个目标航路点、进行同步定位与建图（SLAM）、计算期望轨迹等。机载计算机可能需要处理传感器（如视觉相机和激光雷达）生成的大量数据，这就要求模拟环境具备合理的细节。这是我们所面临的一个挑战性领域，我们借助了诸如虚幻引擎等平台实现的最新渲染技术来应对这一挑战[12]。此外，我们还利用虚幻引擎中的底层管线来检测碰撞。机载计算机通过一组 API与模拟器交互，从而观测传感器数据流和车辆状态，并发送指令。这些 API的设计使得机载计算机无需知晓自身是在仿真环境中运行还是在现实世界中运行。这一点尤为重要，因为它允许用户在模拟器中开发和测试算法，然后直接部署到真实飞行器上而无需额外修改。

AirSim 代码库作为虚幻引擎的插件实现，可以轻松集成到任何 Unreal 项目中。虚幻引擎平台提供了一个丰富的市场，拥有数百个预先制作的详细环境，其中许多是使用摄影测量技术[13]来生成对真实世界场景的合理逼真重建。

接下来，我们将详细介绍模拟器的各个组件。

3.1 车辆模型

AirSim 提供了一个接口，用于将车辆定义为刚体，该刚体可以具有任意数量的执行器以产生力和扭矩。车辆模型包括质量、惯性、线性和角阻力系数、摩擦系数和恢复系数等参数，这些参数由物理引擎用于计算刚体动力学。

形式上，车辆被定义为位于位置{r1,…,rk}的K个顶点和法线{n1,…, nk}的集合，每个顶点受到一个无量纲的车辆特定标量控制输入{u1,…,uk}的作用。假设这些顶点产生的力和扭矩沿其法线方向生成。但需注意，在仿真过程中，位置和法线均可发生变化。

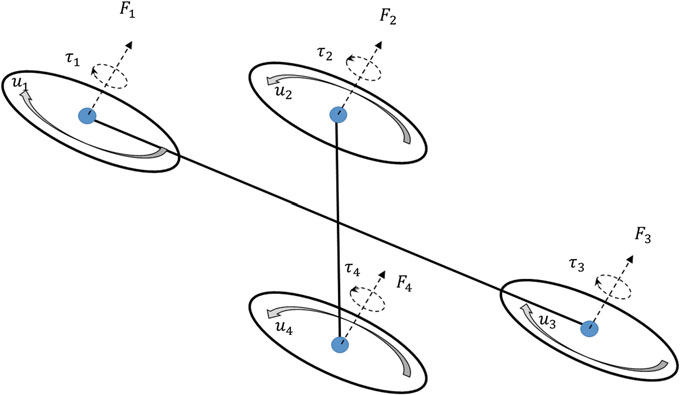
图3展示了四旋翼飞行器如何被表示为四个顶点的集合。控制输入 ui驱动位于四个顶点处螺旋桨的转速。我们使用 [14]计算螺旋桨产生的力和扭矩：

$$
F_i = C_T \rho \omega_{max}^2 D^4 u_i \quad \text{and} \quad \tau_i = \frac{1}{2\pi} C_{pow} \rho \omega_{max}^2 D^5 u_i.
$$

此处$C_T$和$C_{pow}$分别为推力系数和功率系数，基于螺旋桨的物理特性， $\rho$为空气密度，$D$为螺旋桨直径，$\omega_{max}$为每分钟转数的最大角速度。通过允许这些顶点在飞行过程中的运动，可以模拟具有垂直起降（VTOL）能力以及在飞行中改变构型的其他新型四旋翼飞行器。

飞行器模型抽象接口还提供了一种方法来指定机体坐标系中的横截面积，物理引擎可利用该面积计算作用在机体上的线性和角阻力。

3.2 环境

车辆会受到多种物理现象的影响，包括重力、空气密度、气压和磁场。尽管可以建立这些现象的计算成本高的模型以实现很高的精度，但我们主要关注那些精度足够高、并能支持硬件在环实时操作的模型。我们将在下方描述环境中的这些独立组件。

3.2.1 重力

尽管许多模型使用常数来模拟重力，但重力的变化实际上非常复杂，例如 GRACE模型所示[15]。对于大多数地面或低空飞行器而言，这些变化可能并不重要；然而，采用更精确的模型在计算上并不过于昂贵。形式上，我们通过在牛顿万有引力定律上应用二项式定理并忽略高次项，来近似高度$g$处的重力加速度$h$：

$$
g = g_0 \cdot \frac{R_e^2}{(R_e + h)^2} \approx g_0 \cdot \left(1 - \frac{2h}{R_e}\right).
$$

Here $R_e$是地球半径，$g_0$是地表测得的重力常数。

3.2.2 磁场

精确建模复杂物体（如地球）的磁场是一项计算成本较高的任务。由美国国家海洋和大气管理局（NOAA）提出的《世界地磁模型》（WMM）[16]是地球磁场最著名的模型之一。然而，最新的模型WMM2015相当复杂，对于实时应用而言计算开销较大。

我们实现了倾斜偶极子模型，其中假设地球为一个完美的偶极球体[17, 第27页起30]。该模型忽略除一阶项以外的所有项，利用球面几何来推导磁场估计值。此模型使我们能够模拟在空间中移动时磁场的变化，以及诸如极地地区等常出现问题的区域。给定地理纬度 $\theta$、经度 $\phi$和海艸h（距地球表面），我们首先使用以下公式计算磁余纬 $\theta_m$：

$$
\cos\theta_m = \cos\theta \cos\theta_0 + \sin \theta \sin \theta_0 \cos(\phi - \phi_0).
$$

其中 $\theta_0$和 $\phi_0$表示真磁北极的纬度和经度。然后，总磁强度 $|B|$ 计算如下：

$$
|B| = B_0 \left( \frac{R_e}{R_e + h} \right)^3 \sqrt{1 + 3 \cos^2 \theta_m}
$$

此处$B_0$为地球表面磁赤道上磁场的平均值， $\theta_m$为磁余纬，$R_e$为地球的平均半径。接下来，我们通过以下公式确定倾角 $\alpha$和偏角 $\beta$：

$$
\tan \alpha = 2 \cot \theta_m \quad \text{and} \quad \sin \beta =
\begin{cases}
\frac{\sin(\phi - \phi_0)\cos\theta_0}{\sin \theta_m}, & \text{if } \cos\theta_m > \sin \theta_0 \sin \theta \
\frac{\cos(\phi - \phi_0)\cos\theta_0}{\sin \theta_m}, & \text{otherwise}.
\end{cases}
$$

最后，我们可以按如下方式计算磁场矢量的水平场强（H）、纬向（X）、经向（Y）和垂直场（Z）分量：

$$
H = |B| \cos\alpha \quad Z = |B| \sin\alpha \quad X = H \cos\beta \quad Y = H \sin\beta.
$$

3.2.3 气压和密度

由于地球大气层存在许多具有不同特性的独立层次，海艸与大气压力之间的关系十分复杂。首先，我们使用1976年美国标准大气模型T和标准压力P，根据海艸低于51 km的情况，采用公式1.16和1.进行计算；对于51 km以上至86 km的海艸，则切换到表中的模型。然后，空气密度为$P / (R \cdot T)$（其中R为气体常数）。

3.3 物理引擎

物体的运动学状态通过6个量来表示：位置、方向、线速度、线加速度、角速度和角加速度。

物理引擎的目标是根据作用在每个物体上的力和扭矩，计算其下一个运动学状态。我们致力于实现一个高效的物理引擎，能够以高频率（1000Hz）运行其更新循环，这对于实现高速四旋翼控制等实时仿真场景尤为重要。因此，我们实现的物理引擎避免了通用引擎的额外复杂性，从而能够精确控制性能，并做出最符合我们需求的权衡。

3.3.1 线性和角阻力

由于车辆在空气中运动，线性阻力和角阻力对车身的动力学有显著影响。模拟器根据阻力公式计算作用在车身上的线性阻力大小$|F_d|$：[20]：

$$
|F_d| = \frac{1}{2} \rho |v|^2 C_{lin} A.
$$

这里$C_{lin}$是线性空气阻力系数，$A$是飞行器横截面， $\rho$是空气密度。该阻力作用方向与速度矢量$v$相反。

对于任意形状的角阻力计算仍然是一个复杂且计算量大的任务。许多现有的物理引擎使用较小但通常为任意的阻尼常数来替代实际角阻力的计算。我们提供了简单但更优的近似方法来建模角阻力。

考虑物体末端受到角速度 $\omega$作用的一个无穷小表面积 $ds$。由于 $ds$ 所经历的线速度 $dv$ 由 $r_{ds} \times \omega$ 给出，我们现在可以对 $ds$[21, 使用线性阻力方程 161]：

$$
|dF| = \frac{1}{2} \rho |r_{ds} \times \omega|^2 C_{lin} ds, \quad \text{where direction of } dF \text{ is } - r_{ds} \times \omega.
$$

现在，通过在整个表面上积分来计算阻力扭矩：$\tau_d = \int_S r_{ds} \times dF$。为了简化实现，我们将车辆的主体近似为一组连接的面，并且为进一步计算积分，可将这些连接的面进一步近似为一个矩形盒。

3.3.2 加速度

除了阻力和扭矩外，我们还需要考虑作用在相对于重心位置为$r_i$的顶点处车辆上的力$F_i$和扭矩 $\tau_i$（见第3.1节）。因此，我们计算合力和总扭矩如下：

$$
F_{net} = \sum_i F_i + F_d \quad \text{and} \quad \tau_{net} = \sum_i [\tau_i + r_i \times F_i] + \tau_d.
$$

通过应用牛顿第二定律得到线加速度，然后加上重力矢量以计算合加速度，$a = F_{net}/m + g$。机体坐标系中的角加速度由欧拉转动方程给出： $\alpha = I^{-1} \cdot (\tau_{net} - (\omega \times (I \cdot \omega)))$，其中，$I$为惯性张量，$\omega$为角速度，二者均在机体坐标系中。

3.3.3 积分

我们通过积分速度和初始位置来更新物体在时间 $k$到$k+1$时的位置 $p_{k+1}$。一阶积分算法（如欧拉法）虽然实现简单，但会因误差无界而迅速发散。在我们的实现中，我们采用速度Verlet算法而非龙格‐库塔法，因其具有计算成本低和稳定性好的优点，同时仍为二阶方法[22]。形式上，

$$
v_{k+1} = v_k + \frac{a_k + a_{k+1}}{2} \cdot dt \quad p_{k+1} = p_k + v_k \cdot dt + \frac{1}{2} \cdot a_k \cdot dt^2
$$

角速度的更新方式与线速度类似，但姿态的更新并不直接。一种方法是将姿态保持为旋转矩阵，并在每个时间步长进行更新。然而，这会导致缓慢漂移，必须通过定期正交归一化来校正，而这一过程开销较大。另一种替代方法是使用更加高效的四元数来表示旋转，四元数不仅数值稳定且易于归一化。然而，其中一个问题是，在我们的框架中，姿态四元数是在世界坐标系中维护的，而角速度则是在机体坐标系中维护的。为了更新姿态，我们首先计算轴角对$(\alpha dt, u)$，其中 $\alpha dt$是绕单位向量$u$转过的角度。我们可以计算角度$\alpha dt = |\omega| \cdot dt$以及轴向量$u = \omega / |\omega|$。这样就可以计算出等效的姿态变化四元数$q_{dt}$，表示在时间$dt$内的姿态变化。如前所述，$q_{dt}$位于机体坐标系，而$q_k$位于世界参考坐标系。现在的问题是如何将$q_{dt}$加到$q_k$上以得到新的姿态四元数$q_{k+1}$，可以证明该关系由公式$q_{k+1} = q_k \cdot q_{dt}$给出。

3.3.4 碰撞

虚幻引擎提供了一个丰富的碰撞检测系统，针对不同类别的碰撞网格进行了优化，我们直接利用此功能来满足我们的需求。在渲染间隔期间发生的每次碰撞，我们都会接收到撞击位置、撞击法向和穿透深度。我们的物理引擎使用这些数据计算带有库仑摩擦的碰撞响应，以修改线性和角运动学[23]。

3.4 传感器

AirSim提供了加速度计、陀螺仪、气压计、磁力计和全球定位系统的传感器模型。我们所有的传感器模型都以C++头文件形式实现为独立的库，可以在AirSim之外独立使用。

与其他组件一样，传感器模型被表示为抽象接口，因此可以轻松替换或添加新传感器。

3.4.1 气压计

为了模拟气压计，我们使用大气详细模型（第3.2.3节）计算真实压力，并利用高斯‐马尔可夫过程[24]对长时间飞行中压力测量的漂移进行建模，以实现更真实的行为。形式上，如果我们将当前偏差因子表示为$b_k$，则漂移建模如下：

$$
b_{k+1} = w \cdot b_k + (1 - w) \cdot \eta, \quad \text{where: } w = e^{-dt / \tau} \text{ and } \eta \sim N(0, s^2).
$$

此处 $\tau$为该过程的时间常数，在我们的模型中设为1小时。 $\eta$是零均值高斯噪声，其标准差可根据 [25]中提供的数据进行选择。此压力 $p$随后叠加来自零均值高斯分布的白噪声，其标准差根据传感器数据手册（例如MEAS MS56112）设定。最后，我们使用传感器驱动程序所采用的气压公式将压力转换为海艸：

$$
h = \frac{T_0}{a} \left[ \left( \frac{p}{p_0} \right)^{-\left( \frac{a \cdot R}{g} \right)} - 1 \right],
$$

此处$T_0$为参考温度（15◦C），$a = -6.5 \times 10^{-3}$为温度梯度，$g$和$R$分别为重力和比气体常数，$p_0$为当前海平面压力，$p$为测量值。

3.4.2 陀螺仪和加速度计

陀螺仪和加速度计构成惯性测量单元（IMU）的核心[26]。我们通过在真实值上叠加白噪声和随时间变化的偏置漂移来建模这些传感器。对于陀螺仪，给定机体坐标系中的真实角速度 $\omega$，我们计算测量值$\omega_{out}$如下：

$$
\omega_{out} = \omega + \eta_a + b_t, \quad \text{where } \eta_a \sim N(0, r_a) \text{ and } b_t = b_{t-1} + \eta_b, \text{ where } \eta_b \sim N(0, b_0 \sqrt{dt / t_a}).
$$

此处参数$r_a$、偏置$b_0$以及偏置漂移的时间常数$t_a$可通过阿伦方差图或数据手册获得。加速度计输出的计算方式类似，只是我们必须先从世界坐标系中的真实线加速度中减去重力，然后将结果转换到机体坐标系，再添加偏置漂移和噪声。

3.4.3 磁力计

我们使用倾斜偶极子模型来表示地球磁场，如第3.2.2节所述，根据地理坐标计算真实磁场在机体坐标系中的分量，并按数据手册中规定的添加白噪声。

3.4.4 全球定位系统(GPS)

我们的GPS模型模拟了延迟（通常为200毫秒）、较慢的更新速率（通常为50Hz）以及水平和垂直位置误差估计衰减率，以模拟随时间获得定位精度的过程。衰减率通过分别为水平和垂直定位参数化的一阶低通滤波器进行建模。

3.5 视觉渲染

由于高级渲染和精细环境一直是AirSim的关键需求，我们选择了虚幻引擎 4 (UE4)[12]作为我们的渲染平台。UE4提供了多项吸引人的功能，包括其开源特性以及在Linux、Windows和OSX上的可用性。UE4具备一些前沿图形功能，例如基于物理的材质、光度灯光、平面反射、光线追踪距离场阴影、光照半透明等。图1展示了AirSim的截图，突显了其接近照片级真实感渲染的能力。此外，虚幻大型在线市场提供了各种预制作精细环境，其中许多是通过摄影测量技术创建的。

4 实验

我们进行实验主要是为了评估四旋翼飞行器在真实世界中的飞行特性与在AirSim中同一车辆仿真之间的接近程度。我们还将一些传感器模型与现实世界传感器进行了对比评估。

硬件平台 ：真实世界飞行使用安装在Flamewheel四旋翼机架上的Pixhawk v2飞控控制器，并搭配一台技嘉5500 Brix运行Ubuntu 16.04。传感器测量值记录在Pixhawk设备本身上。

我们在AirSim中使用测量的物理参数配置模拟四旋翼，并根据传感器数据表配置模拟传感器模型。AirSim MavLinkTest 应用程序用于对真实世界飞行和模拟飞行执行可重复的外部控制。

轨迹评估 ：我们在模拟器中以两种不同的模式飞行四旋翼飞行器：（1）边长为5 米的方形轨迹；（2）半径为10米的圆形轨迹。然后使用完全相同的指令飞行真实飞行器。对于仿真和真实世界飞行，我们均收集车辆在本地北东地坐标系中的位置及相应的时间戳。

图4c 和 b 显示了模拟飞行与真实飞行中位置的时间序列。其中，横轴表示时间，纵轴表示X和Y方向的偏移。我们还计算了真实世界轨迹与仿真轨迹之间的对称豪斯多夫距离。结果表明，无论是圆形轨迹（模拟与真实世界之间的豪斯多夫距离：1.47 米）还是方形轨迹（模拟与真实世界之间的豪斯多夫距离：0.65 米），仿真轨迹与真实世界轨迹都相当接近。

我们还展示了图4a和d中圆形和方形路径的视觉对比。模拟轨迹用紫色线条表示，实际轨迹用红色线条表示。定性上可以看出，真实世界车辆和模拟车辆的跟踪轨迹较为接近。微小差异可能由多种因素引起，例如积分误差、车辆模型近似和轻微随机风。

传感器模型 ：除了评估整个模拟流程外，我们还研究了独立组件模型，即气压计（MEASMS5611‐01BA）、磁力计（霍尼韦尔 HMC5883）和惯性测量单元（IMU）（应美盛 MPU 6000）。需要注意的是，当前的模拟GPS模型较为简单，因此我们仅关注上述三个更复杂的传感器模型。对于上述每种传感器，我们均使用制造商指定的数据表来设置传感器模型中的参数。

• IMU ：我们测量了车辆在静止状态和飞行中的加速度计和陀螺仪读数。我们观察到，当车辆处于静止状态时，特性相似（陀螺仪：模拟方差2.47e −7 rad²/s²，真实世界方差6.71e −7 rad²/s²；加速度计：模拟方差1.78e −4 m²/s⁴，真实世界方差1.93e −4 m²/s⁴），但在飞行中车辆的观测方差远高于模拟值（加速度计：模拟1.75e −3 m²/s⁴ 对比 真实世界9.46 m²/s⁴）。这可能是由于在真实世界中电机运行时机体振动，而该现象尚未在AirSim中建模所致。

• 气压计 ：我们周期性地将传感器在两个固定高度之间移动：地面水平，然后抬升至178厘米（仿真和真实世界中均如此）。图5a展示了测量值（绿色为模拟的，蓝色为真实世界），我们观察到信号具有相似的特性。请注意，模拟与真实世界压力之间的偏移是由于真实世界中的绝对压力与仿真中的绝对压力不同所致。此外，由于温度升高导致中间部分未被模拟。总体而言，模拟的传感器特性与真实传感器非常吻合。

• 磁力计 ：我们将车辆放置在地面上，然后将其旋转90◦四次。图5b显示了真实世界和模拟的测量值，并突出显示它们在特征上非常相似。

5 结论与未来工作

AirSim提供高保真物理和视觉仿真，能够低成本地生成大量训练数据，用于构建机器学习模型。AirSim API的设计允许在模拟器上开发算法，然后无需修改即可部署到真实飞行器上。AirSim的核心组件，包括物理引擎、车辆模型、环境模型和传感器模型，均被设计为可独立使用，且对AirSim外部的依赖最小，易于扩展。AirSim的设计灵感源于开发能够在现实世界中运行的自主智能体的强化学习算法这一目标。

在实时仿真中模拟真实世界是一项具有挑战性的任务。有许多方面可以改进。目前，我们尚未模拟更丰富的碰撞响应或高级地面交互模型，但通过实现我们的物理引擎接口以支持NVIDIA PhysX并利用诸如物理子步进等功能，未来可能实现这些特性。此外，除了虚幻引擎直接提供的功能外，我们尚未模拟相机传感器中的各种异常现象。我们计划在未来添加高级噪声模型和镜头模型。由于障碍物导致的GPS信号衰减也尚未模拟，我们计划使用光线追踪方法来实现这一功能。我们还计划为固定翼飞行器增加更先进的风效应和热仿真。我们的可扩展性API在设计时已考虑到上述未来工作，也可用于实现其他类型的飞行器。