时间复杂度，插入排序，冒泡排序，选择排序

什么是数据结构和算法

数据结构

数据结构就是我们把现实中大量而复杂的问题以特定的数据类型和特定的存储结构保存到主存储器(内存)中；
数据结构就是研究个体的存储以及个体关系的存储；就研究数据如何存储到内存中去的。
数据结构 = 个体{特定数据类型} + 个体的关系{特定的存储关系}

算法

在此基础上为实现某个功能(比如查找某个元素，删除某个元素，对所有元素进行排序)而
执行的相应操作，这个相应的操作叫算法。
算法 = 对存储数据的操作。
算法就是解题的方法和步骤。
衡量算法的标准：

• 1.时间复杂度
  大概程序要执行的次数，而非执行的时间
• 2.空间复杂度
  算法执行过程中大概所占用的最大内存
• 3.难易程度
• 4.健壮性

概括

数据结构的地位
数据结构是软件中最核心的课程
程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言

什么是时间复杂度

就是近似于约等于算法总的执行的次数；
说白了时间复杂度就是近似约等于算法中常数操作的次数；
时间复杂度使用O(n)（可以读big O n）来表示
在一个算法之中，算法常数操作次数 * 每个数的常数操作的时间 = 算法总执行时间；

什么是常数操作

一个样本执行和数量没有关系，每次都是固定时间完成，叫做常数操作。
比如两个数加减乘除赋值的操作;比如
int i =好几亿；//固定时间完成
上面这样说可能还是有点不清楚，通过一个例子详细介绍一下；
比如我现在要打印一个链表上面的所有数据，假设链表的数据是下面这样排列
（数据不是下面这样有规律的排列，这里只是为了看数据方便）

i	0	1	2	3	4	5	…
value	-190	0	39	56	89	900	…

假设从链表中拿出一个数需要花t1秒，迭代一下需要花t2秒；那么打印这个链表所有数据总共需要多长时间呢？
这个链表上面有N个数据，现在我们来总结一下，从N个数据中打印 i 个数总共所需要的时间是多少？
i = 0，需要用时间等于 (t1+t2) x 1秒
i = 1，需要用时间等于 (t1+t2) x 2秒
i = 2，需要用时间等于 (t1+t2) x 3秒
i = 3，需要用时间等于 (t1+t2) x 4秒
…
…
…
i = N-1，需要用时间等于 (t1+t2) x N秒
所以，打印N个数的链表需要用总时间 : (Nx(N+1)/2) x (t1+t2)，
其中 t1+t2 可以理解为操作一个数所用的平均时间(常数操作时间)，
使用函数可以这样表示f(n)=(n²+n)/2*t‘;
其中f(n)可以表示算法总的执行时间；t =t1+t2，看做常数操作时间；
时间复杂度我们使用T(n)来表示；
这个时候就有 T(n) = O(f(n)),其中f(n)中我们只要高阶项，不要低阶项，不要高阶项的系数，最后f(n) = n² ,所以时间复杂度T(n) = O( n² )；
这里补充一下利用数学极限思想理解一下，当n无穷大的时候，这个n² 是不是约等于(n ²+n)/2 {别忘了此处这个值是常数操作时间的总次数},因此我们可以一般使用程序执行的常数时间次数来作为时间复杂度；某种意义上来说，它也近似反映了程序的执行时间；

教科书上时间复杂度的定义

若有某个辅助函数f(n)，使得当n趋近于无穷大时，$T(n)/f(n)$的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(f(n))，它称为算法的渐进时间复杂度，简称时间复杂度。
用如下公式表示：
$$O(n)={\int }_0^{\infty }\frac{T(n)}{f(n)}\ne 0$$

我们想一想上面的 (n²+n)/2 *t相当于T(n) ;n² 相当于f(n)吗;它们求极限值肯定不是0，结果应该等于1

以上就是我对时间复杂度的再次理解认识，不知道小伙伴懂了没；

时间复杂度为O(n²)的三种排序算法

选择排序

大体思想是这样的：
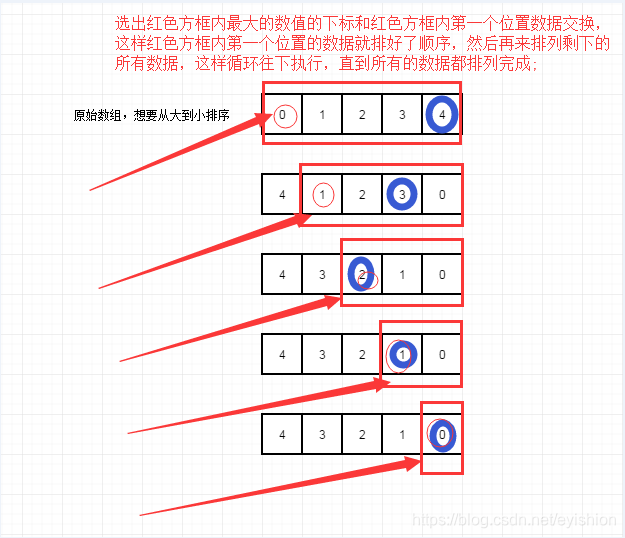
1，先从所有数据中选择数值最大（或最小）的数，记住下标；
2，跟第一个位置的数据进行交换，这样第一个位置排好了顺序，（最大值或最小值放首位了）；
3，然后在从剩下的数据中选择数值最大（或最小）的数，记住下标，和剩下的数据中的第一个位置交换，这样剩下的数据中第一个位置也排好了顺序…依次这样循环执行到所有数据都排好了顺序；
转化成图表示如下：

使用代码完成想选择排序的过程：java实现

	//选择排序的实现
	private static void selectSort(int[] arr) {

		for (int i = 0; i < arr.length; i++) {//从0 ~ arr.length-1中选择出最大值的下标，和位置交换数据
			int index = i;//index用来记住最大值的下标，然后和i位置交换
			for (int j = i + 1; j < arr.length; j++) {
				if (arr[index] < arr[j]) {
					index = j;
				}
			}
			//交换两个位置数据的方法
			Utils.swap(arr, index, i);
		}

	}

冒泡排序

大体思想是这样的（以从大到小排列举例）：
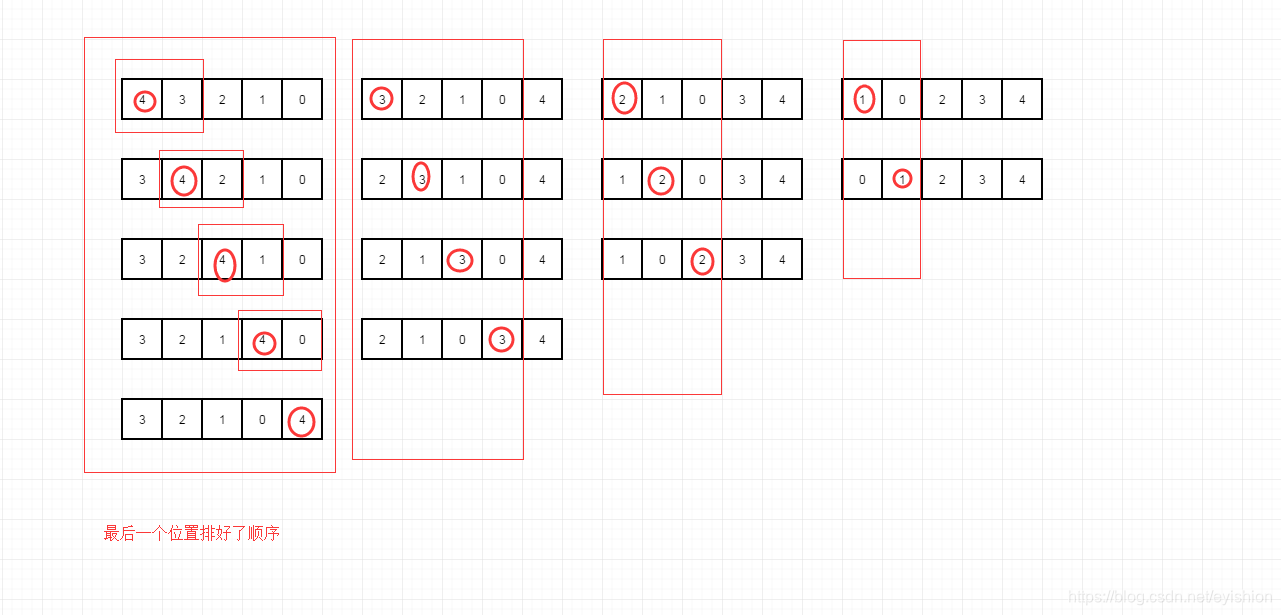
1，从第一个位置数和下一个位置数进行两两比较，如果比下一个位置数大，就交换，否则就保持顺序不变
2，再比较第二个位置的两个数据，如果比下一个位置数大，就交换，否则就保持顺序不变，
…
以此类推，按照上面的规则一直往下去运行，直到所有的数据都排好位置；
这个过程就像气泡一点一点往上浮起来一样，是不是很神似；
转化成图表示如下：

使用代码实现如下：java实现

	// 冒泡排序的实现
	public static void bubbleSort(int[] arr) {

		for (int i = arr.length - 1; i >= 0; i--) {

			for (int j = 0; j < i; j++) {// 冒泡 0 ~ i之间像气泡一样往上浮，排好了之后i会往下减
				// 前面的数大，就交换
				if (arr[j] > arr[j + 1]) {
					Utils.swap(arr, j, j + 1);
				}
			}
		}
	}

插入排序

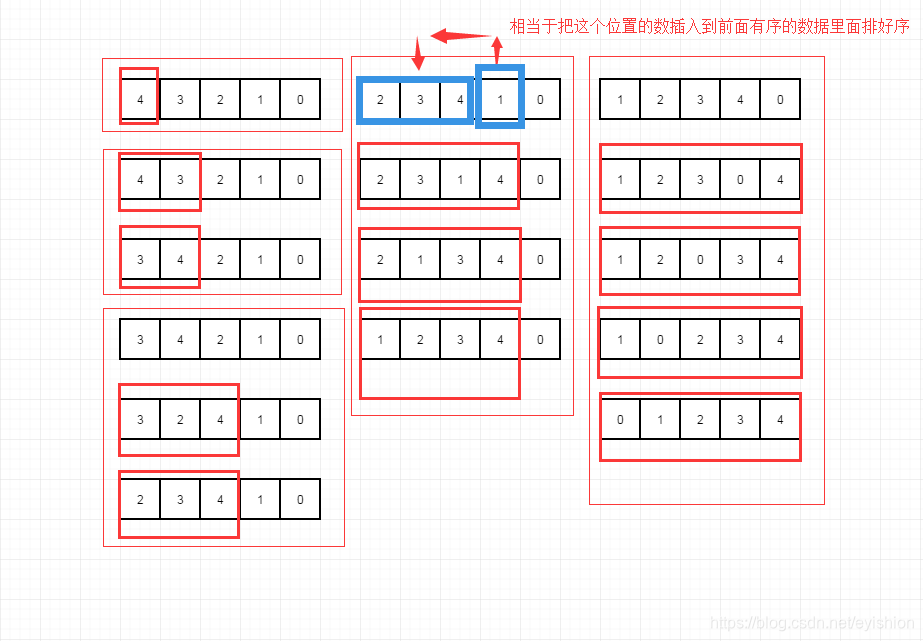
这种排序的总体思想就是往已经排好序的数据中，插入一个数据，使得数据重新排列好.
使用图形来表示（从小到大的排序为例），好好看看图示中箭头的地方，你就会明白插入排序了，一张图说清楚了；

使用代码来实现这个过程：java代码实现

	// 插入排序实现
	public static void insertSort(int[] arr) {

		for (int i = 0; i < arr.length; i++) {

			// 0~1 , 0~2 ,... , 0 ~ (arr.length-1)
			// 条件是j越界了吗？&&这个数大于前一个数吗
			for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
				Utils.swap(arr, j, j + 1);
			}
		}
	}

另外上面所有代码都用到了交换方法，它的代码如下：

	public static void swap(int[] arr, int x, int y) {
		int temp = arr[x];
		arr[x] = arr[y];
		arr[y] = temp;
	}