【JZOJ5781】秘密通道

最新推荐文章于 2022-10-30 18:00:00 发布

原创

最新推荐文章于 2022-10-30 18:00:00 发布 · 1.6k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#spfa #最短路 #模拟赛

本文介绍了一道名为‘秘密通道’的问题，涉及一副包含墙、起点、终点和空地的地图。主角可以移动、发射子弹创建秘密通道以及通过通道。任务是求出从起点到终点的最短时间。给出了使用SPFA算法解决此问题的思路，以及错误示例和正确解题方法。

problem

Description
有一副n*m的地图，有n*m块地，每块是下列四种中的一种：
墙：用#表示，墙有4个面，分别是前面，后面，左面，右面。
起点：用C表示，为主角的起点，是一片空地。
终点：用F表示，为主角的目的地，是一片空地。
空地：用 . 表示。
其中除了墙不能穿过，其他地方都能走。

主角有以下3种操作：
1.移动到相邻的前后左右的地方，花费一个单位时间。
2.向前后左右其中一个方向发射子弹，子弹沿直线穿过，打在最近的一堵墙的一面，然后墙的这面就会形成一个开口通往秘密通道。同一时间最多只能有两个开口，若出现有3个开口，出现时间最早的开口会立即消失。该操作不用时间。
3.可以从一个与开口相邻的空地跳进去，进入秘密通道，从另外一个开口正对的空地跳出来。这个过程花费一个单位时间。

地图四周都是墙，问主角最少用多少时间从C走到F。C和F
只会出现一次。

Input
第一行输入两个正整数n，m。
接下来n行，每行m个字符描述地图。

Output
输出1个整数，表示最短时间完成路途。如果无解输出nemoguce

Sample Input
Input 1
4 4

#

.F

C.

#

Input 2
6 8

#

.##..F

C.##..

..#…

…..

#

Input 3
4 5

#

C#.

F

#

Sample Output
Output 1
2
Output 2
4
Output 3
nemoguce

Data Constraint
对于50%的数据，4≤ n,m≤ 15。
对于100%的数据，4≤ n,m≤ 500。

Hint
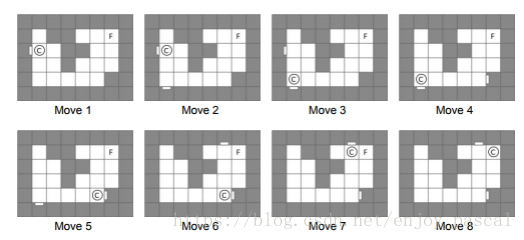
总共用到8次操作，时间之和为4。如下图所示
1.向左射一枪，在(3,1)的右面出现开口。
2.向下射一枪，在(6,2)的上面出现开口。
3.向左从(3,1)进入秘密通道，从(6,2)中出来，到达(5,2)。用1单位时间。
4.向右射一枪，在(5,7)的左面出现开口，(3,1)右面的开口消失。
5.走进(6,2)的开口，出来到(5,6)。用1单位时间。
6.向上射一枪，在(1,6)的下面出现开口。
7.经过秘密通道，走到(2,6)。用1单位时间。
8.走到终点。用1单位时间。