补充:
本文是关于《Sklearn 与 TensorFlow 机器学习实用指南》的学习笔记,基于八、降维 - 【布客】Sklearn 与 TensorFlow 机器学习实用指南 第二版,感谢译者
本文和原文的区别:
本文会更精简、系统地表述书中概念,会对书中未介绍的陌生概念加以解释,每行我都会添加注释,介绍具体做了什么。
后续会持续更新所有章节
正文开始 ~
————————————————
当数据集的维度过高时,模型训练难度增大、过拟合风险上升且计算资源消耗剧增。这种现象通常被称为维数灾难(curse of dimentionality)。
应对策略:
降维:降低特征维度,减少特征数量,简化问题。
选择重要的维度,丢弃不太重要的:
例如,对于 MNIST 图片集,由于图片四周边缘部分的像素几乎总是白的,完全可以将这些像素从你的训练集中扔掉而不会丢失太多信息。
利用相邻像素的高度相关性,整合不同的维度:由于相邻像素的高度相关性,整合维度可以在不丢失太多信息的情况下有效地降低数据维度。
例如:
1. 空间金字塔
概念:将图像划分为不同尺度的子区域(如不同大小的块),并为每个子区域提取特征。
特点:
利用相邻像素的空间相关性,从多个尺度上捕捉图像信息。
减少维度的同时保留多尺度特征。
2. 局部特征提取
概念:通过滑动窗口或其他方法在图像中提取局部特征(如SIFT、HOG)。
特点:
捕捉相邻像素的局部信息,同时减少全局维度。
可以通过降维技术(如PCA)进一步压缩特征向量。
3. 亚像素卷积
概念:将多个低分辨率图像的特征组合起来,恢复高分辨率的输出。
特点:
利用相邻像素的信息来提高分辨率,同时减少计算复杂度。
常用于超分辨率重建等任务。
4. 特征金字塔网络(FPN)
概念:通过不同层次的卷积操作提取多尺度特征图。
特点:
利用低层特征图中的细节信息和高层特征图中的语义信息,构建多层次的特征表示。
有效降低维度的同时保留丰富的图像内容。
5.平均池化(Average Pooling)
概念:将相邻像素进行平均或求和操作,得到低分辨率的特征图。
特点:
简单有效地降维,同时保留局部信息。
常用于减少计算量和参数数量。
6. 图像压缩与量化
概念:将相邻像素合并或进行某种形式的量化编码。
特点:
减少存储空间和传输带宽的需求。
可应用于实时视频处理和流媒体等场景。
降维的特点:
1. 在降维过程中可能会丢失某些信息,应该先尝试使用原始的数据来训练,如果训练速度太慢的话再考虑使用降维
2. 通过降维去除噪声或冗余特征(这种情况通常不会发生,它只会加快你训练的速度)
3. 降维将高维数据映射到二维或三维空间,便于直观展示和理解,便于可视化(Visualization)
在这一章里,会介绍:
两种主要的降维方法:投影(projection)和流形学习(Manifold Learning),
三种流行的降维技术:主成分分析(PCA),核主成分分析(Kernel PCA)和局部线性嵌入(LLE)。
1. 维度灾难
在低维空间中,大量数据点可能会集中在某些区域(如中心区域),在高维空间中,数据更倾向于分布在边界处(一个简单的理解思路参考https://www.kpfans.com/article/LmWKKJXWB3.html),且随机选取的点之间距离变得更大,主要是维度增加导致的数据稀疏性和欧氏距离的平方和累积效应(在高维空间中,即使每个坐标轴上的变化相对较小,由于平方和的积累效应,最终导致欧几里得距离显著增大)共同作用的结果。
维度过高的影响:
1. 距离度量失真:高维空间中点之间的相对距离变得不明显,难以区分。
2. 过拟合问题加剧:高维空间下,新增的新实例可能远离任何训练实例,这使得预测的可靠性远低于较低维度数据,模型可能过度适应训练数据,导致泛化能力下降,增加过拟合风险。
3. 计算复杂度上升:处理大量特征会显著增加计算时间和资源消耗。
补充:
理论上来说,维数爆炸的一个解决方案是增加训练集的大小从而达到拥有足够密度的训练集。不幸的是,在实践中,达到给定密度所需的训练实例的数量随着维度的数量呈指数增长。如果只有 100 个特征并且假设它们均匀分布在所有维度上,那么如果想要各个临近的训练实例之间的距离在 0.1 以内,需要比宇宙中的原子还要多的训练实例。
2. 降维的主要方法:投影与流形学习
这两种主要方法适用的情况:训练实例并不是在所有维度上均匀分布的。许多特征几乎是常数,而其他特征则高度相关。结果,所有训练实例实际上位于(或接近)高维空间的低维子空间内。
例如:左图,所有训练实例的分布都贴近一个平面:这是高维(3D)空间的较低维(2D)子空间。将每个训练实例垂直投影到这个子空间上,就可以得到的新 2D 数据集。如右图
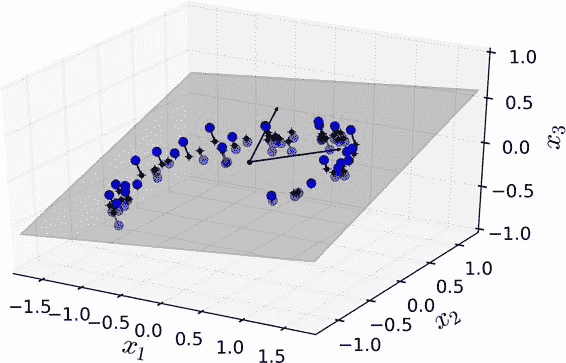
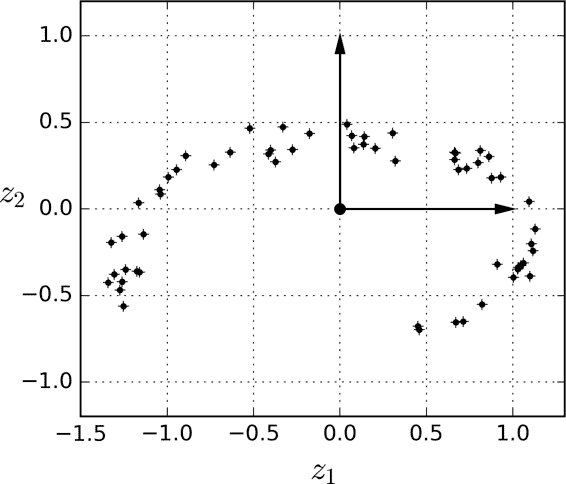
上述方法就是投影,但投影并不总是降维的最佳方法。在很多情况下,子空间可能会扭曲和转动,例如瑞士滚动玩具数据集
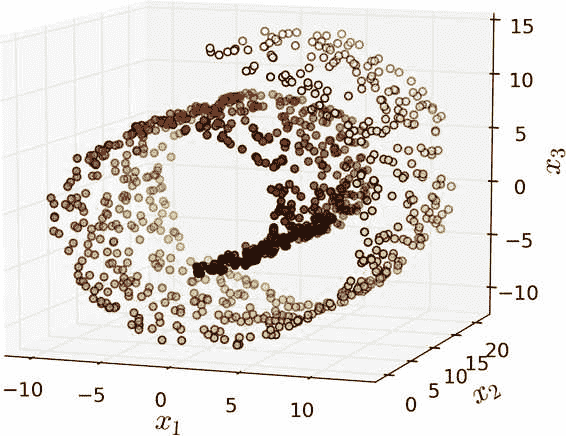
简单地将数据集投射到一个平面上(例如,直接丢弃x3方向)会将瑞士卷的不同层叠在一起,如左图 。但是,真正想要的类似右图的 2D 数据集。





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 1303
1303

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










