import tensorflow as tf
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
随机变量
#tf.random_normal(shape,mean=0.0,stddev=1.0,dtype=tf.float32)
#tf.truncated_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32)
#tf.random_uniform(shape,minval=0,maxval=None,dtype=tf.float32)
#这几个都是用于生成随机数tensor的。尺寸是shape
#random_normal: 正太分布随机数,均值mean,标准差stddev
#truncated_normal:截断正态分布随机数,均值mean,标准差stddev,不过只保留[mean-2*stddev,mean+2*stddev]范围内的随机数
#random_uniform:均匀分布随机数,范围为[minval,maxval]
# 生成2*2的矩阵
x=tf.random_normal((2,2))
y=tf.truncated_normal((2,2),stddev=1, mean=0)
z=tf.random_uniform((2,2),-1,1)
with tf.Session() as sess:
print(sess.run(x))
print("------------------------------------")
print(sess.run(y))
print("------------------------------------")
print(sess.run(z))
[[ 1.1302718 0.15843017]
[-2.0472283 -1.4401605 ]]
------------------------------------
[[ 0.04470472 0.44935352]
[ 1.3003236 -0.7512413 ]]
------------------------------------
[[-0.35371923 -0.508945 ]
[ 0.8172362 -0.35298085]]
概率分布
离散型变量和概率质量函数(PMF) mass
连续型变量和概率密度函数(PDF) density
bernoulli分布 (两点分布)
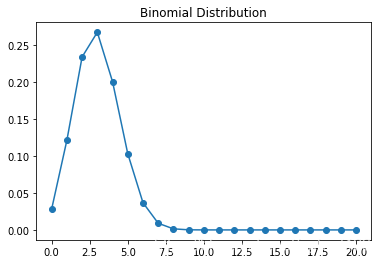
Binomial Distribution 二项分布(n重Bernoulli分布)
P(x=k)=(n!k!(n−k)!)pk(1−p)(n−k)P(x=k) = (\frac{n!}{k!(n-k)!})p^k(1-p)^{(n-k)}P(x=k)=(k!(n−k)!n!)pk(1−p)(n−k)
E(X) = np, Var(X) = np(1−p)
n = 10
p = 0.3
k = np.arange(0, 21)
binomial = stats.binom.pmf(k, n, p)
plt.plot(k, binomial, 'o-')
plt.title('Binomial Distribution')
plt.show()
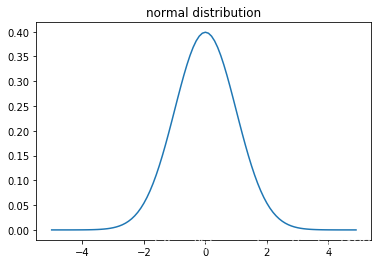
normal distribution高斯分布(正态分布)
N(x;μ,σ2)=12πσ2exp(−(x−u)22σ2)N(x; \mu, \sigma^2) = \sqrt{\frac{1}{2\pi\sigma^2}}exp(-\frac{(x-u)^2}{2\sigma^2})N(x;μ,σ2)=2πσ21exp(−2σ2(x−u)2)
mu = 0
sigma = 1
x = np.arange(-5, 5, 0.1)
y = stats.norm.pdf(x, mu, sigma)
plt.plot(x, y)
plt.title('normal distribution')
plt.show()
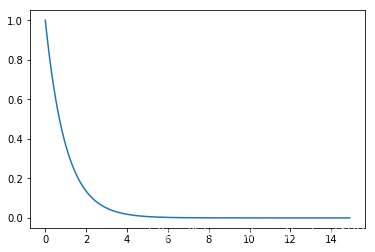
Exponential Distribution 指数分布
p(x;λ)=λe−λxp(x; \lambda) = \lambda e^{-\lambda x}p(x;λ)=λe−λx
E(x)=1λE(x) = \frac{1}{\lambda}E(x)=λ1, Var(x)=1λ2Var(x) = \frac{1}{\lambda^2}Var(x)=λ21
lamda = 0.5
x = np.arange(0, 15, 0.1)
y = stats.expon.pdf(x)
plt.plot(x, y)
plt.show()
# logistic sigmoid
# softmax
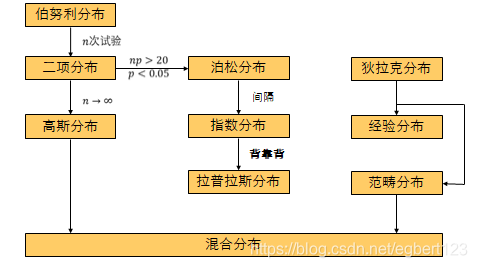
概率论小结
贝叶斯规则
P(y | x) --> P(x | y)
P(x∣y)=P(x)P(y∣x)P(y)P(x | y) =\frac{P(x)P(y | x)}{P(y)}P(x∣y)=P(y)P(x)P(y∣x)
P(y)=∑P(y∣x)P(x)P(y) = \sum P(y|x)P(x)P(y)=∑P(y∣x)P(x)
信息论(在决策树中有应用)
信息论是应用数学得分支,主要研究得是对一个信号包含信息得多少进行量化
信息论的基本想法是一个不太可能的事件居然发生了,要比一个非常可能的事件发生能提供更多的信息。
信息量
I(x)=−logP(x)I(x) = -logP(x)I(x)=−logP(x)
当log以e为底时,单位时奈特nats,1nats是以1/e的概率观测到一个事件的信息量
当log以2为底时,单位时比特bit,或者香农
举个例子:抛硬币正面向上的信息量为 entropy=−log12=1bitentropy = -log\frac{1}{2} = 1bitentropy=−log21=1bit
信息熵(Entropy) : 信源含有的信息量是信源发出的所有可能消息的平均不确定性,信源所含有的信息量。
信息熵度量了信息的不确定性,消息越不确定,信息熵越大。
info(D)=−∑(pi)log2(pi)info(D) = -\sum(p^i)log_2(p^i)info(D)=−∑(pi)log2(pi)
举个例子: 抛一枚硬币的信息熵为info(D)=−0.5log20.5−(1−0.5)log2(1−0.5)=1info(D) = -0.5log_2 0.5 - (1-0.5)log_2 (1-0.5) = 1info(D)=−0.5log20.5−(1−0.5)log2(1−0.5)=1
结构化概率模型(暂时不知道结构化概率模型会在哪些地方用到)
有向模型
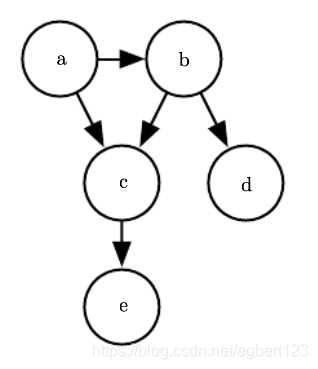
p(a,b,c,d,e)=p(a)p(b∣a)p(c∣a,b)p(d∣b)p(e∣c)p(a,b,c,d,e) = p(a)p(b|a)p(c|a,b)p(d|b)p(e|c)p(a,b,c,d,e)=p(a)p(b∣a)p(c∣a,b)p(d∣b)p(e∣c)
无向模型
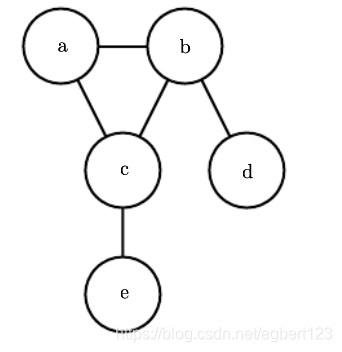
p(x)=1Z∏ϕ(i)(ζ(i))p(x) = \frac{1}{Z}\prod\phi^{(i)}(\zeta^{(i)})p(x)=Z1∏ϕ(i)(ζ(i))
p(a,b,c,d,e)=1Zϕ(1)(a,b,c)ϕ(2)(b,d)ϕ(3)(c,e)p(a,b,c,d,e) = \frac{1}{Z}\phi^{(1)}(a,b,c)\phi^{(2)}(b,d)\phi^{(3)}(c,e)p(a,b,c,d,e)=Z1ϕ(1)(a,b,c)ϕ(2)(b,d)ϕ(3)(c,e)
其中两两之间有边连接的称为团,每个团伴随一个因子ϕ\phiϕ,同时为了除以归一化常数ZZZ来得到归一化概率
无向模型很容易看出因子之间的关系,比如a,b,c相互影响,a和e通过c间接相互影响。























 28
28

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








