代码随想录第46天|139.单词拆分多重背包理论基础背包总结

最新推荐文章于 2025-12-23 20:02:55 发布

原创最新推荐文章于 2025-12-23 20:02:55 发布 · 341 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法

文章目录

单词拆分
- 思路：
- 代码
多重背包≈0-1背包
- 题目
- 代码
背包总结

单词拆分

3 在这里插入图片描述

思路：

在这里插入图片描述

代码

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        HashSet<String> set = new HashSet<>(wordDict);
        boolean[] dp=new boolean[s.length()+1];
        dp[0]=true;
        //先背包体积再物品
        for(int j=1;j<=s.length();j++){
            for(int i=0;i<j;i++){
                if(dp[i]==true&&set.contains(s.substring(i,j))){
                    dp[j]=true;
                    break;//快一点
                }
            }
        }
        return dp[s.length()];
    }
}

多重背包≈0-1背包

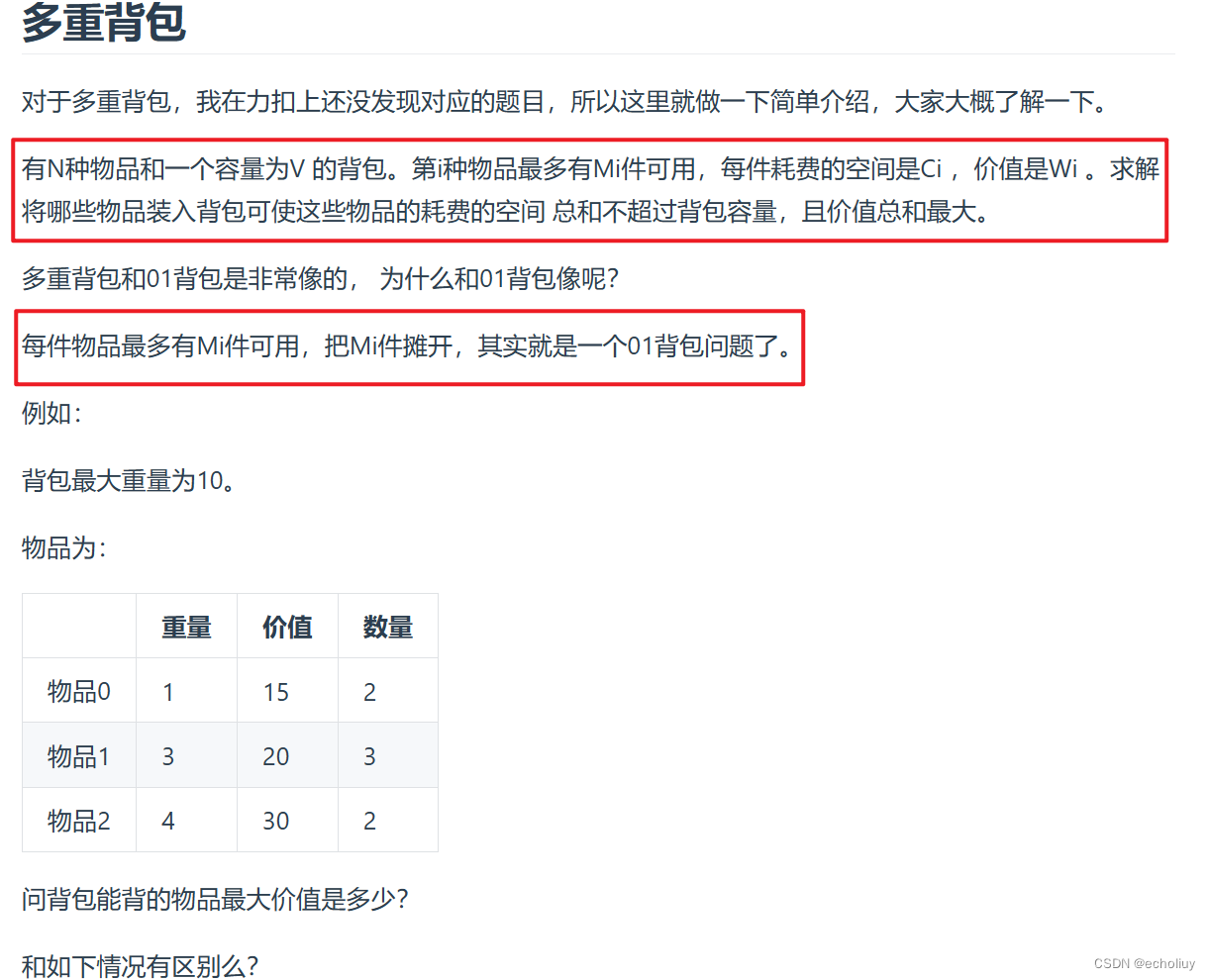
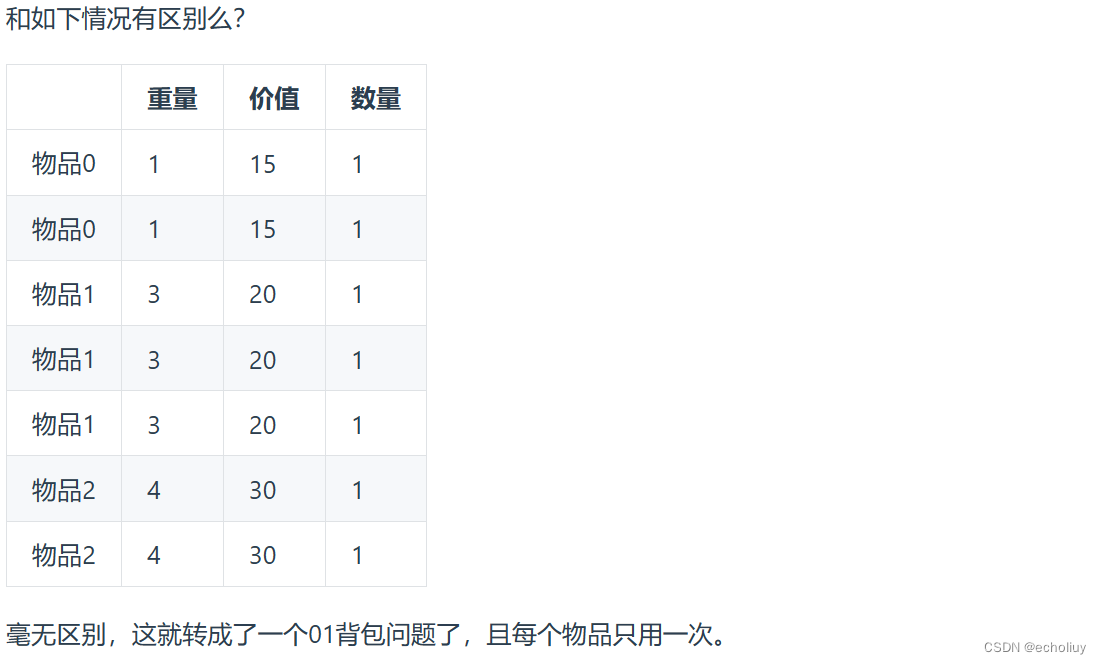
在这里插入图片描述

题目

在这里插入图片描述

代码

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        // int 
        while(sc.hasNextInt()){
            int c = sc.nextInt();
            int n = sc.nextInt();
            int[] weight = new int[n];
            int[] value = new int[n];
            int[] numbers = new int[n];
            for (int i = 0;i < n;i++) {
                weight[i] = sc.nextInt();
            }
            for (int i = 0;i < n;i++) {
                value[i] = sc.nextInt();
            }
            for (int i = 0;i < n;i++) {
                numbers[i] = sc.nextInt();
            }
            int[] dp=new int[c+1];
            for(int i=0;i<n;i++){
                for(int j=c;j>=weight[i];j--){
                // 每个i物品的循环都考虑k个
                    for(int k=1;k<=numbers[i]&&(j-k*weight[i])>=0;k++){
                        dp[j]=Math.max(dp[j],dp[j-k*weight[i]]+k*value[i]);
                    }
                }
            }
            System.out.println(dp[c]);
            
        }
    }
}