代码详解：一文掌握神经网络超参数调优

全文共7002字，预计学习时长14分钟或更长

神经网络在通信行业和研究中的使用十分常见，但令人遗憾的是，大部分应用都未能产出足以运行其他算法的高性能网络。

应用数学家在开发新型优化算法时，喜欢进行功能测试，有时也被称为人造景观。人造景观有助于从以下方面比较各算法的性能：

· 收敛（算出答案的速度）

· 精准度（与正确答案的接近程度）

· 稳健性（是否所有功能表现优良，或仅一小部分如此）

· 综合表现（如概念复杂度）

浏览有关功能优化测试的维基词条，就会发现有些功能很难对付。很多功能因找出优化算法的问题而被广泛使用。但本文将讨论一项看似微不足道的功能——Beale功能。

Beale功能

Beale功能如下图所示：

Beale功能是测试功能的原因在于，它能在坡度极小的平坦区域内评估调优算法的性能。在这种情况下，基于坡度的优化算法程序难以有效地学习，因此很难达到最小值。

本文接下来将按照GitHub库里的Jupyter笔记本教程开展讨论，以得出解决人造景观的可行方式。该景观类似于神经网络的损失平面。训练神经网络的目的是通过某种形式的优化找到损失平面上的最小值——典型的随机坡度减少。

在学习使用高难度的优化功能后，本文读者能充分应对施行神经网络时遇到的实际问题场景。

测试神经网络前，首先需要给功能下定义能并找出最小值（否则无法确定为正确答案）。第一步（引进相关软件包后），在笔记本中定义Beale功能：

已知此案例中（由我们构想）最小值的大概范围及栅极网孔的步长，第二步设置功能边界值。

根据以上信息制作一组点状网孔栅极，就可以找出最小值。

现在，得出（非常）初步的结论。

然后使用scipy.optimize功能，得出答案。

答案结果如下：

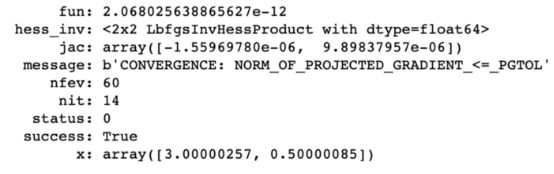
答案似乎是（3，0.5）。如果把这些值填入等式，这确实是最小值（维基上也显示如此）。

接下来进入神经网络部分。

神经网络的优化

神经网络可以被定义为一个结合输入并猜测输出的系统。幸运的话，在得出被称作“地面实况”的结果后，将之与神经网络的各种输出进行比对，就能计算错误。因此，神经网络首先进行猜测，然后计算错误功能；再次猜测，将错误最小化；再次猜测，直到错误最小化。这就是优化。

神经网络中最常使用的优化算法是GD（gradient descent，坡降）类型。坡降中使用的客观功能正是想缩至最小的损失功能。

本教程的重头戏是Keras，因此再回顾一下。

Keras复习