[leetcode 1095] 山脉数组中查找目标值

分析

首先可以看到这是一个山脉，他的大体结构类似于一个上山和一个下山的过程，上山是一个递增数组，下山是一个递减数组，如下图。。。。

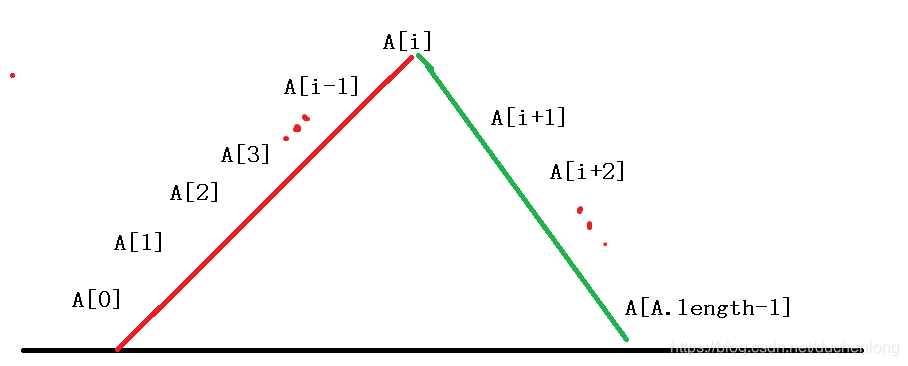
其次，题中明确说明了，访问数组元素的下标次数不能多于100次，但是数组长度最大为10000，所以说我们用变量肯定是不行的。
这时就可以使用二分法了，访问次数不能多于100次，那么二分法访问100次可以是多大的范围呢?
假设我们每次查找只访问一次，那么一共可以访问的范围是 --> 2的100次方；
要是我们每次查找访问两次，一共可以访问的长度也是 --> 2的50次方，这是远远大于10000的，所以 我们可以用二分来解决。

思路

一开始看到这个问题，直接用二分法来做的话，因为这是一个先递增再递减的数组，我们不能确定mid处的数据是递增数组中的数还是递减区间的一个数，我们在直接二分的过程中我们很难判断。

我们再看这个山中数据的集合，他都是单纯的地址或者递减，在递增或者递减的区间中不存在相等的值。所以说目标数据的范围一定不会超过它本身，也就是[0,target] 或者 [len - target, len)，这样就把我们的问题分成了两个子区间，但是我们同样也无法保证我们这两个子区间是单调递增或者是单调递减的。

所以我们再进行二分法查找之前，我们需要先确定山顶元素的位置，然后就可以把原区间分成两个单独的子区间，这两个子区间都是满足单调性的区间。我们再分别在这两个区间中进行二分查找就Ok了。这里还需要注意，这两个区间一个是递增，一个是递减，二分法的写法会有所不同，需要分开来写。

找到山顶位置

	//[left,right],参数中是一个左闭右闭区间
	int MountTopFind(MountainArray& mountainArr,int left,int right) {
        while(left < right) {//这块不能用 <= 
            int mid = (left + right) / 2;
            //mid处山比后面的低，左区间肯定不存在山顶,mid位置肯定不是山顶
            if(mountainArr.get(mid) < mountainArr.get(mid + 1)) left = mid + 1;
            else right = mid;//mid处的山比后面的山高,mid位置可能是山顶
        }
        return left;
    }

这里我们需要注意一点，就是我们在找山顶的时候，我们需要确定该如何缩小左右区间的范围

• (mountainArr.get(mid) < mountainArr.get(mid + 1) ：当前查找的位置是mid，他比后面位置的高度小，所以说mid肯定不是山顶，山顶在mid的后面。我们就需要更新left的位置
• (mountainArr.get(mid) > mountainArr.get(mid + 1)：当前查找的位置是mid，相比于后面的高度，他比较高，所以说mid位置可能是山顶。我们在更新的时候right = mid，不能覆盖了mid位置
• 第三，这种情况时不可能出现=的，由题意可知，前后两个数据都是不相等的

需要区别的是，while循环判断的条件不能是<=，因为当左右区间位置相等时，这个位置就是山顶，我们需要返回山顶元素。在while循环结束后，left = right，我们返回一个就可以了。

山底到山顶 递增区间二分查找

 	int BinaryFindLeft(int target,MountainArray& mountainArr,int left,int right) {
        while(left <= right) {
            int mid = (left + right) >> 1;
            int num = mountainArr.get(mid);
            if(num == target) return mid;
            else if(num > target) right = mid - 1;
            else left = mid + 1;
        }
        return -1;
    }

这就是一个简单的左闭右闭递增区间的二分查找
这里可以先建立一个变量保持mid高度的值，可以减少对该高度的访问次数。。。。

山顶道山底 递减区间二分查找

	int BinaryFindRight(int target,MountainArray& mountainArr,int left,int right) {
        while(left <= right) {
            int mid = (right + left) >> 1;
            int num = mountainArr.get(mid);
            if(num == target) return mid;
            else if(num > target) left = mid + 1;
            else right = mid - 1;
        }
        return -1;
    }

这是一个左闭右闭递减区间的二分查找

源码

/**
 * // This is the MountainArray's API interface.
 * // You should not implement it, or speculate about its implementation
 * class MountainArray {
 *   public:
 *     int get(int index);
 *     int length();
 * };
 */

class Solution {
public:
    int findInMountainArray(int target, MountainArray &mountainArr) {
        int len = mountainArr.length();
        int mountTop = MountTopFind(mountainArr,0,len-1);
        //在山顶元素的两边开始查找
        int ans = BinaryFindLeft(target,mountainArr,0,mountTop);
        return (ans != -1) ? ans : BinaryFindRight(target,mountainArr,mountTop+1,len-1);//左边没有找到，就在右边找
    }

    //找到山顶元素
    int MountTopFind(MountainArray& mountainArr,int left,int right) {
        int top = 0;
        while(left < right) {
            int mid = (left + right) / 2;
            //mid处山比后面的低，左区间肯定不存在山顶,mid位置肯定不是山顶
            if(mountainArr.get(mid) < mountainArr.get(mid + 1)) left = mid + 1;
            else right = mid;//mid处的山比后面的山高,mid位置可能是山顶
        }
        return left;
    }

    //递增区间的二分查找
    int BinaryFindLeft(int target,MountainArray& mountainArr,int left,int right) {
        while(left <= right) {
            int mid = (left + right) >> 1;
            int num = mountainArr.get(mid);
            if(num == target) return mid;
            else if(num > target) right = mid - 1;
            else left = mid + 1;
        }
        return -1;
    }

    //递减区间二分查找
    int BinaryFindRight(int target,MountainArray& mountainArr,int left,int right) {
        while(left <= right) {
            int mid = (right + left) >> 1;
            int num = mountainArr.get(mid);
            if(num == target) return mid;
            else if(num > target) left = mid + 1;
            else right = mid - 1;
        }
        return -1;
    }
};