机器学习基础 - [第一章：单变量线性回归]（7）线性回归模型的梯度下降

1、使用梯度下降算法来求解线性回归模型的局部最小值

在前面，我们已经得到了单变量线性回归模型的假设函数$h_{\theta }(x)$和采用均方误差的代价函数$J({\theta }_0,{\theta }_1)$，如图1右半部分所示，现在我们用梯度下降来求解使代价函数获得局部最小的对应参数值，如图2所示：
将假设函数的具体形式代入梯度下降算法的核心公式，更新${\theta }_0$和${\theta }_1$

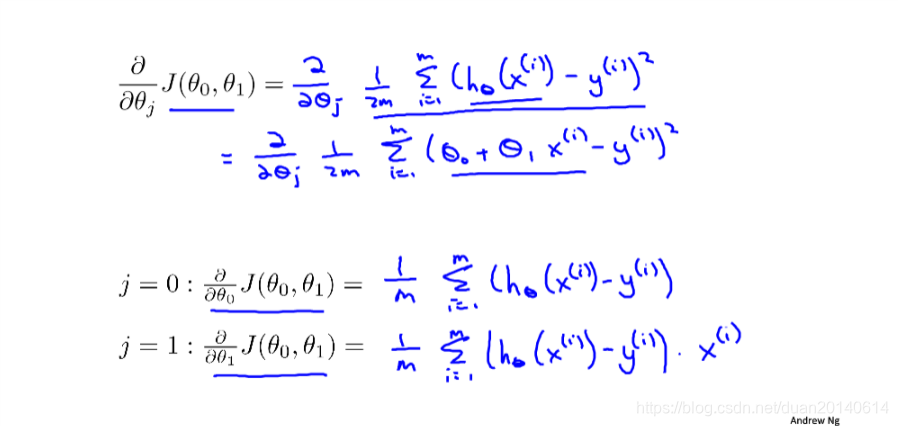
循环参数的更新过程，直至收敛：

收敛的可视化过程如下所示：

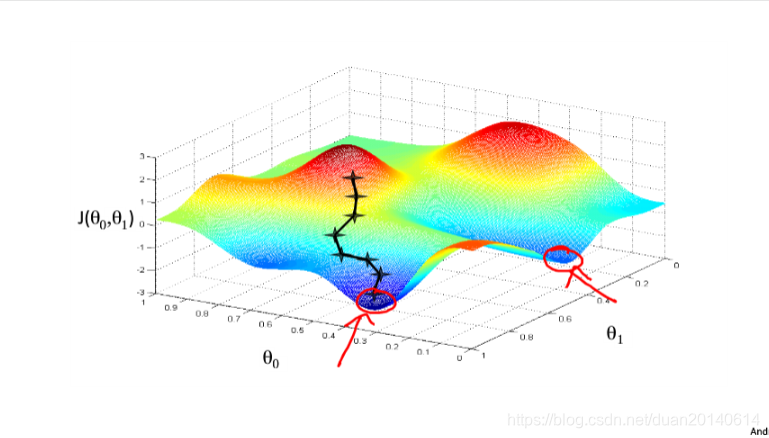
2、线性回归模型的代价函数的特殊性

从图3中我们可以发现一个问题，当代价函数有多个局部最小值时，只要在梯度下降的过程中方向出现了一点偏差，最后收敛到的局部最小值可能完全不同，如上图红色箭头所示。
但是，对于线性回归模型而言，根本不会存在这个问题，因为他的代价函数是一个凸函数（图4所示），仅有一个局部最小值，

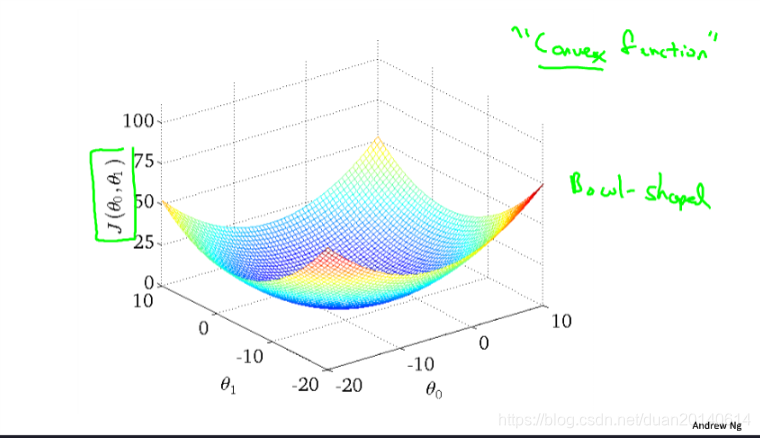
3、梯度下降算法在执行过程中假设函数对数据的拟合情况

（1）初始值

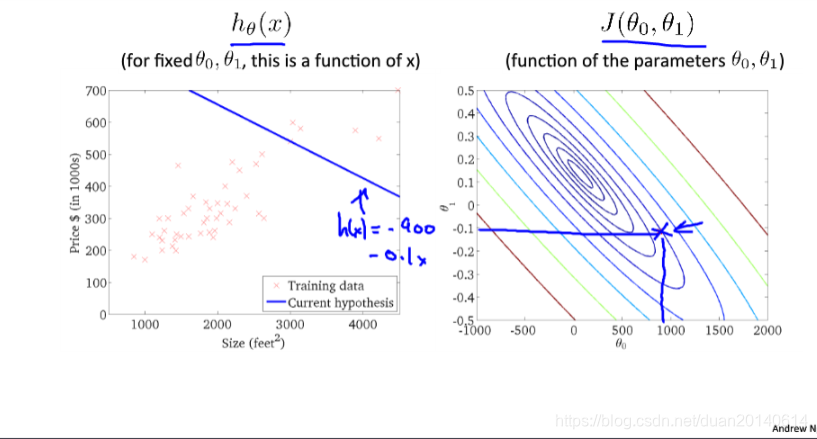
（2）第一次迭代

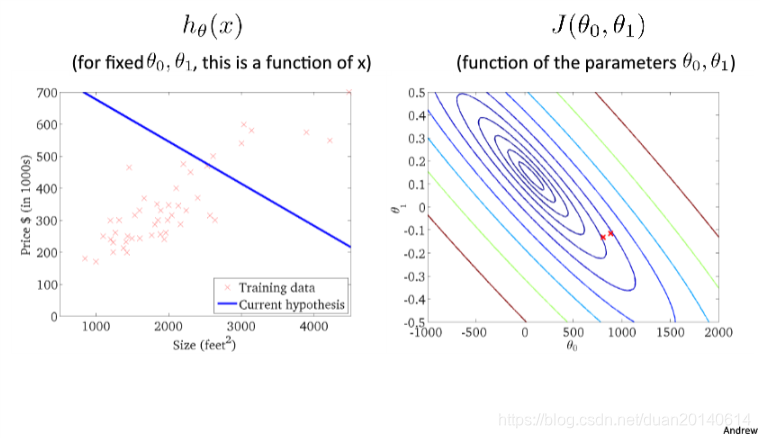
（3）第二次迭代

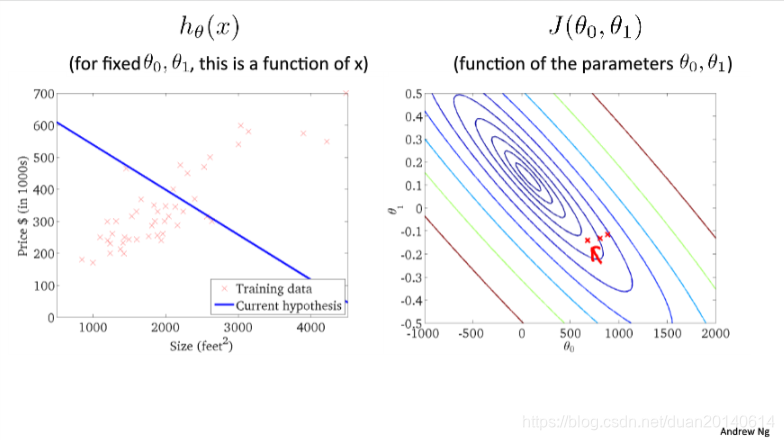
（4）第三次迭代

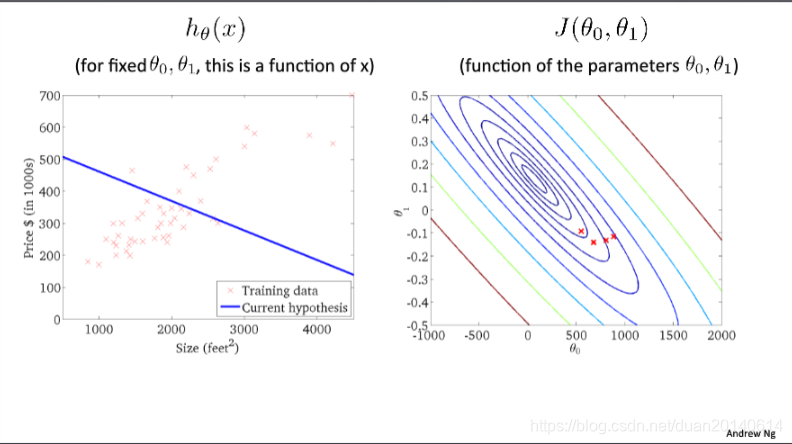
（5）第四次迭代

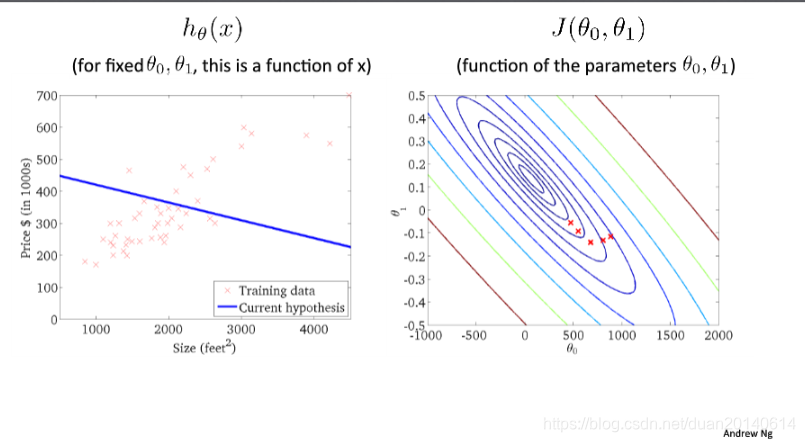
（6）第五次迭代

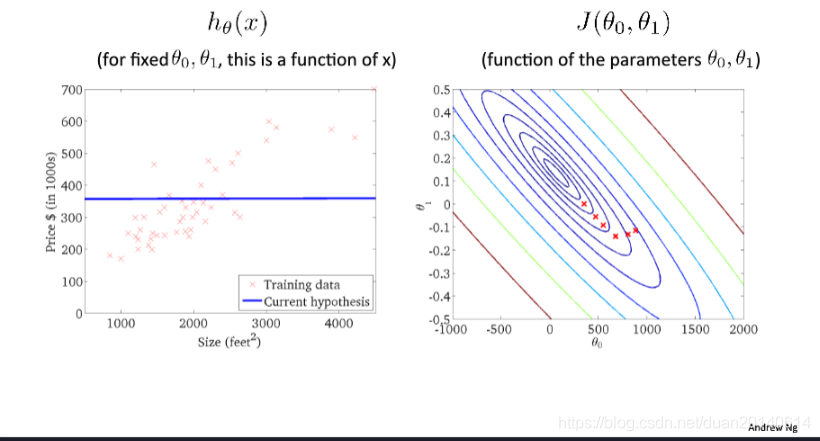
（7）第六次迭代

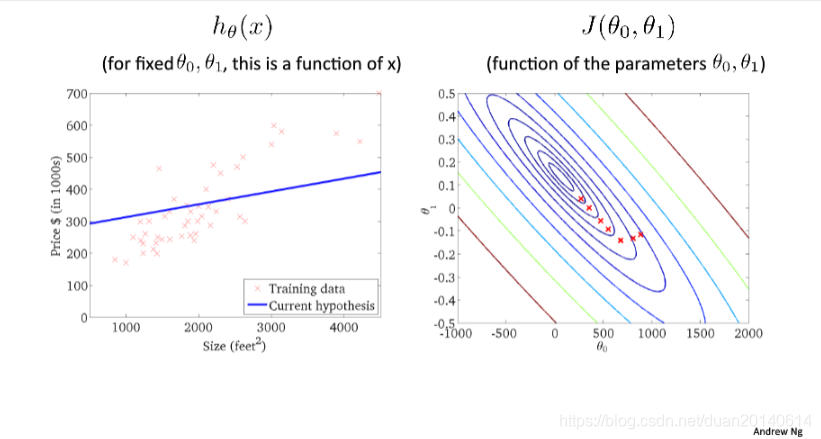
（8）第七次迭代

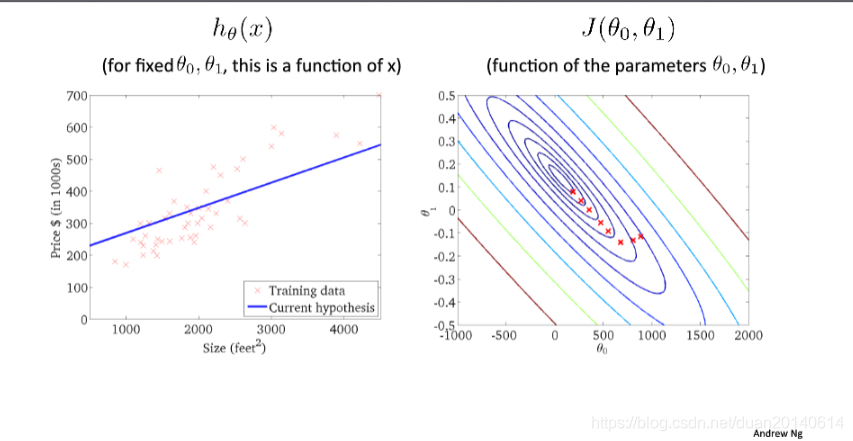
（9）第八次迭代

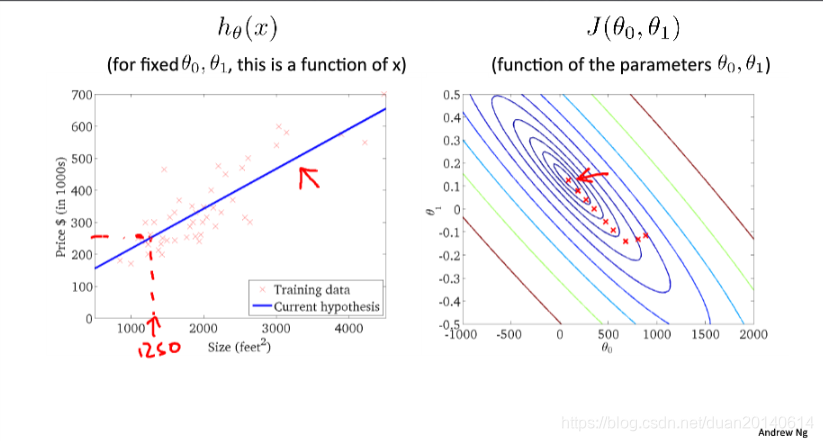
4、批量梯度下降（batch gradient descent，BGD）

批量梯度下降是指每一次迭代更新参数时，使用所有的训练样本。

5、参数求解的其他方法

事实上，参数学习还有很多方法，比如正规方程法，它和梯度下降的区别在于：
正规方程在小规模数据集上速度很快，而梯度下降法在大规模数据集上更有优势。