通用算法 -[排序算法] - 堆排序_怎么将大顶堆排成线性对数-优快云博客

本文深入解析堆排序算法，从最大堆和最小堆的概念出发，详细介绍了堆排序的具体步骤，包括构建大顶堆、交换堆顶元素并调整堆结构的过程。通过动图直观展示排序流程，并提供了完整的实现代码，最后分析了算法的时间复杂度和空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、算法思想

先回顾以下堆的概念
堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式。
在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立。
例子：
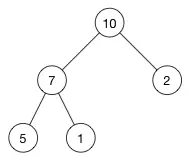
在这里插入图片描述
这是一个最大堆，因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。
堆的实际存储结构是一个数组，i表示根节点的索引，i2+1和i2+2分别表示根节点i的左右子节点。
上图所示的堆实际存储为
[10，7，2，5，1]

堆排序就是先将数组中元素构建成一个最大堆，然后把堆顶的元素与最后一个元素交换，交换之后破坏了堆的特性，我们再把堆中剩余的元素再次构成一个大顶堆，然后再把堆顶元素与最后第二个元素交换….如此往复下去，等到剩余的元素只有一个的时候，此时的数组就是有序的了。
为方便理解我还准备了动图：
在这里插入图片描述

2、实现代码

 // 堆排序
void headSort(int* arr int length) {
    
        //构建大顶堆
        for (int parent = (length - 2) / 2; parent >= 0; parent--) 			   	
        { 
            shiftDown(arr, parent, length - 1);
        }
        
        //进行堆排序
        for (int i = length - 1; i >= 1; i--) {
            // 把堆顶元素与最后一个元素交换
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            // 把打乱的堆进行调整，恢复堆的特性
            shiftDown(arr, 0, i - 1);
        }
    }

        //下沉操作
 void shiftDown(int*  arr, int parent, int length) {
        //临时保存要下沉的元素
        int temp = arr[parent];
        //定位左孩子节点的位置
        int child = 2 * parent + 1;
        //开始下沉
        while (child <= length) {
            // 如果右孩子节点比左孩子大，则定位到右孩子
            if(child + 1 <= length && arr[child] < arr[child + 1])
                child++;
            // 如果孩子节点小于或等于父节点，则下沉结束
            if (arr[child] <= temp ) break;
            // 父节点进行下沉
            arr[parent] = arr[child];
            parent = child;
            child = 2 * parent + 1;
        }
        arr[parent] = temp;
    }
}