1、算法由来
我们知道,简单插入排序在数据规模较小和数据基本有序时十分高效。
那如果数据规模较大,并且无序时,有什么样的方法可以提高简单插入排序的效率呢?
希尔排序正是为此而生,它通过构造(1)小规模数据和(2)让数据基本有序的条件来达到高效排序。
2、算法思想
希尔排序的基本思想是分组进行插入排序。即每次根据增量序列(从大到小)中的一个增量值,将数组划分成若干组,然后对这若干组分别进行简单插入排序。直到数组有序位置。
以数组array=[5,7,8,3,1,2,4,6]为例,希尔算法的具体过程如下:
(1)首先它把较大的数据集合分割成若干个小组(逻辑上分组),然后对每一个小组分别进行插入排序,此时,插入排序所作用的数据量比较小(每一个小组),插入的效率比较高。
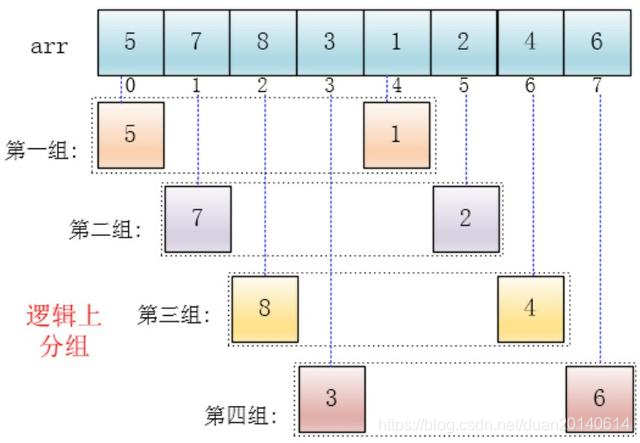

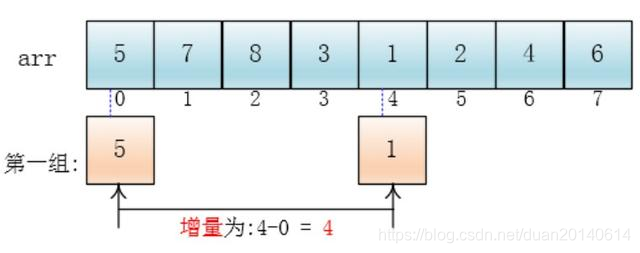
可以看出,他是按下标相隔距离为4分的组,也就是说把下标相差4的分到一组,比如这个例子中a[0]与a[4]是一组、a[1]与a[5]是一组…,这里的差值(距离)被称为增量
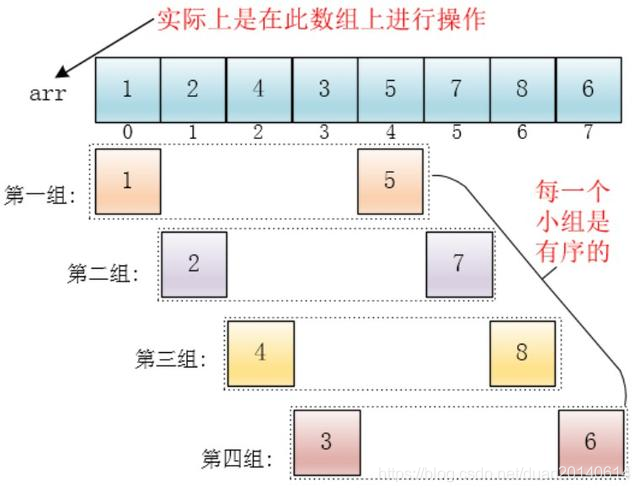
(2) 每个分组进行插入排序后,各个分组就变成了有序的了(整体不一定有序)
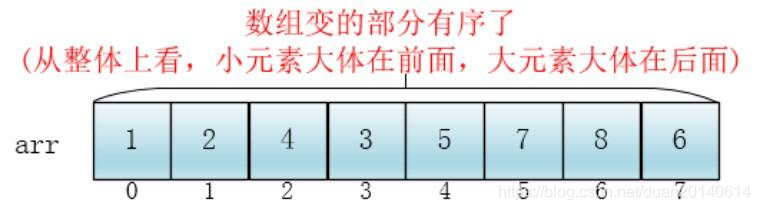
此时,整个数组变的部分有序了(有序程度可能不是很高)
(3) 然后缩小增量为上个增量的一半:2,继续划分分组,此时,每个分组元素个数多了,但是,数组变的部分有序了,插入排序效率同样比高。
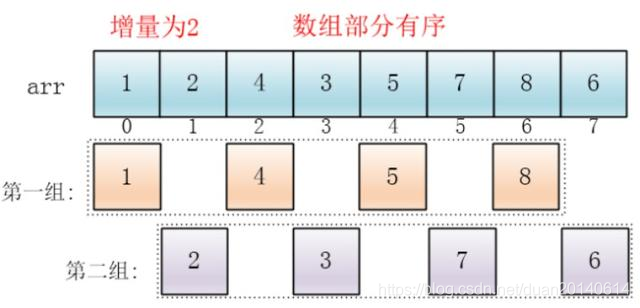
同理对每个分组进行排序(插入排序),使其每个分组各自有序
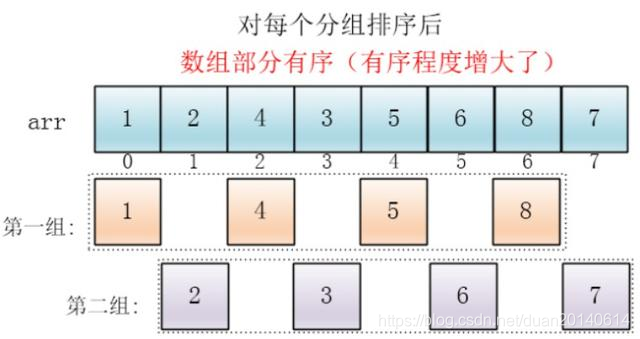
(4) 最后设置增量为上一个增量的一半:1,则整个数组被分为一组,此时,整个数组已经接近有序了,插入排序效率高
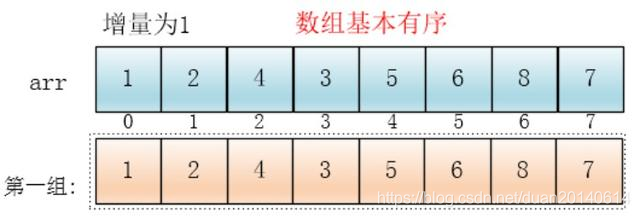
同理,对这仅有的一组数据进行排序,排序完成
3、代码实现
希尔排序分组实现:
template<typename T>
void shellSort(T* array,int len){
//对数组进行分组,最开始的增量(gap)为数组长度的一半;
for (int gap = len / 2; gap >= 1; gap = gap / 2){
//对以gap为增量形成的分组进行插入排序
for (int i = gap; i < len; i++){
insertSort(array, i, gap);
}
}
}
组内进行插入排序实现:
template<typename T>
void insertSort(T* array, int i, int gap){
/*
将array[i]插入到所在分组的正确位置上;
array[i]所在的分组:
...array[i-gap*2],array[i-gap],array[i],array[i+gap],array[i+gap*2]...
*/
/*写法1:
T inserted = array[i];
int j = i - gap;
while (j >= 0 && inserted < array[j]){
array[j + gap] = array[j];
j -= gap;
}*/
/*写法2:*/
T inserted = array[i];
int j;
for (j = i - gap; j >= 0 && inserted < array[j]; j -= gap){
array[j + gap] = array[j];
}
array[j + gap] = inserted;
}
4、算法分析
- 时间复杂度:希尔排序的复杂度和增量序列是相关的。
{1,2,4,8,...}\{1,2,4,8,...\}{1,2,4,8,...}这种序列并不是很好的增量序列,使用这个增量序列的时间复杂度(最坏情形)是O(n2)O(n^2)O(n2),Hibbard提出了另一个增量序列{1,3,7,...,2k−1}\{1,3,7,...,2^k-1\}{1,3,7,...,2k−1},这种序列的时间复杂度(最坏情形)为O(n1.5)O(n^{1.5})O(n1.5),Sedgewick提出了几种增量序列,其最坏情形运行时间为O(n1.3)O(n^{1.3})O(n1.3),其中最好的一个序列是{1,5,19,41,109,...}\{1,5,19,41,109,...\}{1,5,19,41,109,...}。 - 空间复杂度:O(1)O(1)O(1)。
- 稳定性:简单插入虽是稳定的,但希尔排序是不稳定的,详细原因见下图。
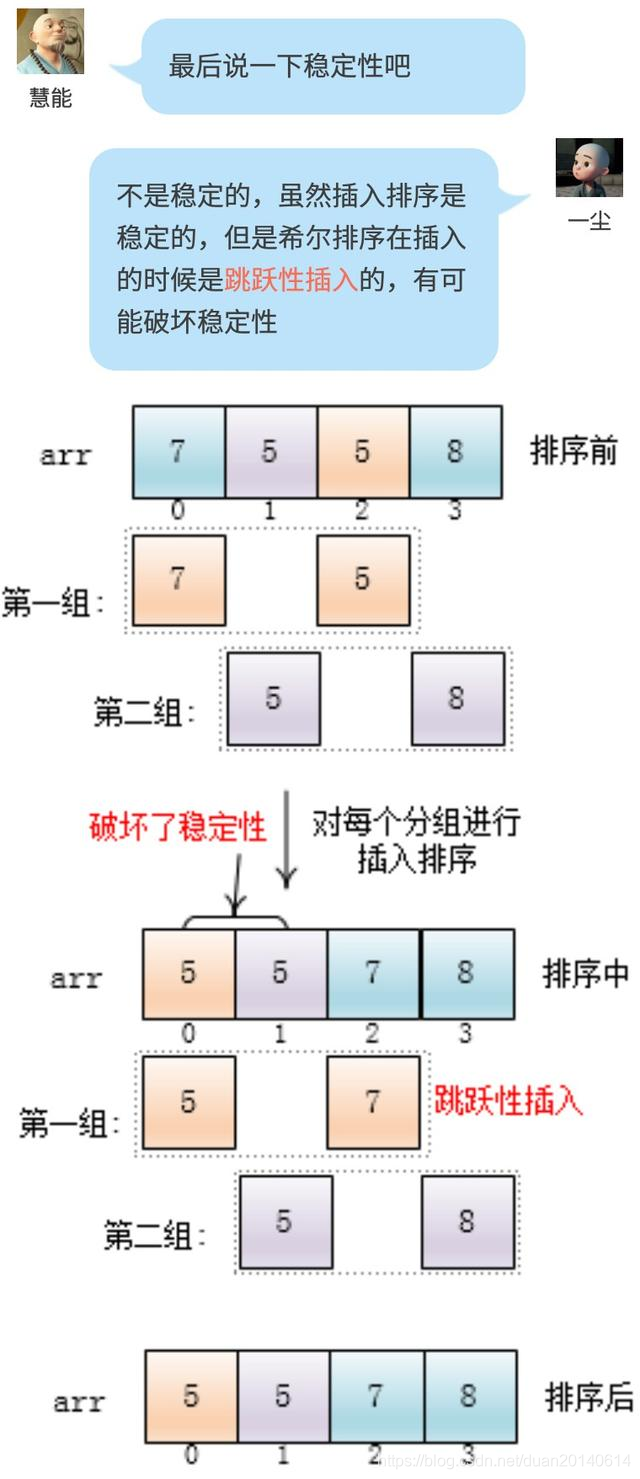





 希尔排序是一种改进的插入排序算法,通过分组进行插入排序以提高效率。它先按照一定的增量序列对数组进行逻辑分组,然后对每个小组进行插入排序。随着增量逐渐减少,数据变得部分有序,从而提升排序速度。最终,当增量为1时,数组近乎有序,插入排序效率较高,完成排序。希尔排序的时间复杂度与增量序列有关,空间复杂度为O(1),但该算法不稳定。
希尔排序是一种改进的插入排序算法,通过分组进行插入排序以提高效率。它先按照一定的增量序列对数组进行逻辑分组,然后对每个小组进行插入排序。随着增量逐渐减少,数据变得部分有序,从而提升排序速度。最终,当增量为1时,数组近乎有序,插入排序效率较高,完成排序。希尔排序的时间复杂度与增量序列有关,空间复杂度为O(1),但该算法不稳定。

















 483
483

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










