【递归、搜索、回溯】专题二：二叉树dfs

最新推荐文章于 2025-12-07 21:20:15 发布

原创最新推荐文章于 2025-12-07 21:20:15 发布 · 701 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法 #数据结构 #c++ #力扣 #leetcode

递归、搜索、回溯专栏收录该内容

6 篇文章

订阅专栏

一、计算布尔二叉树的值

2331. 计算布尔二叉树的值 - 力扣（LeetCode）

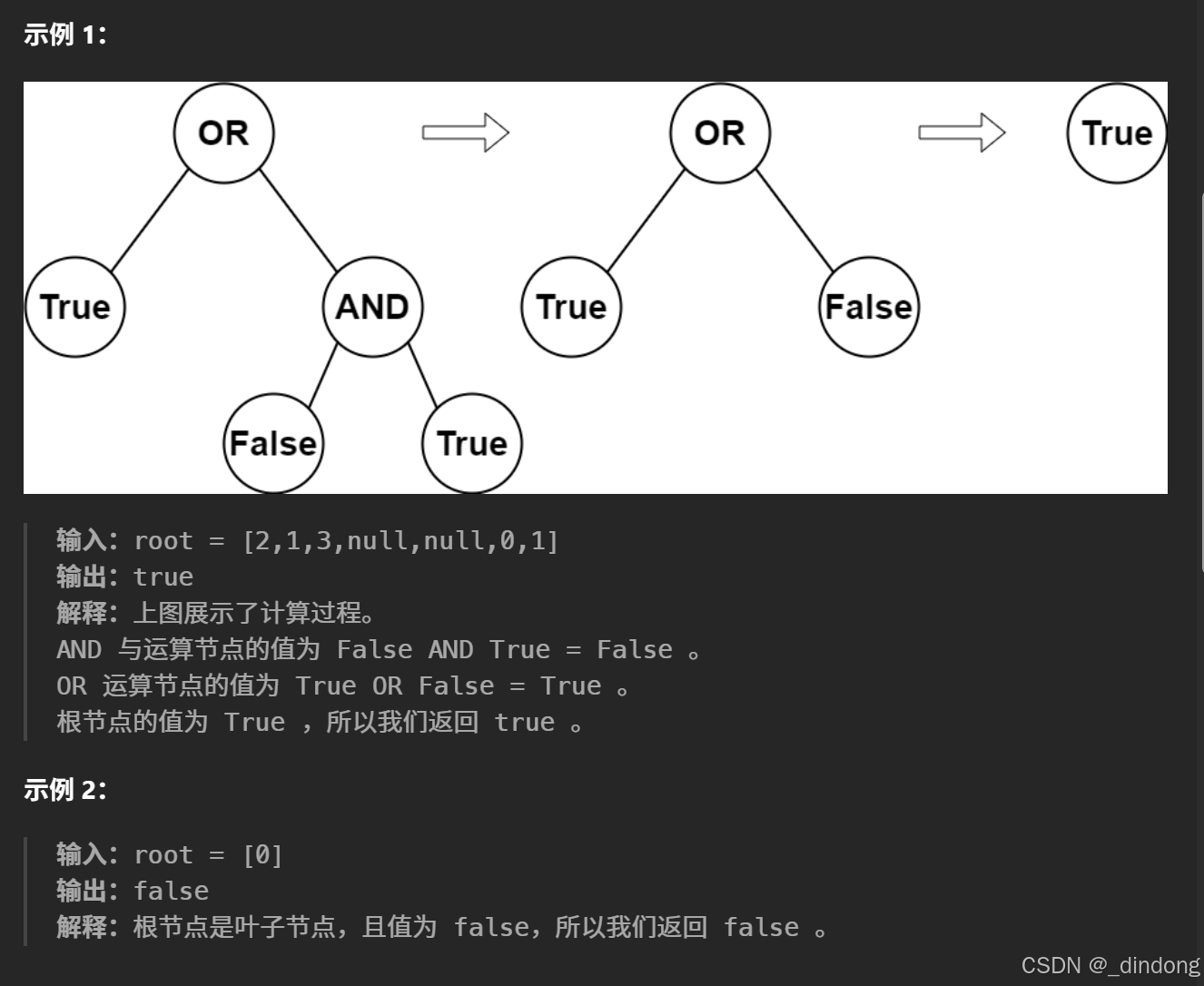
后序遍历

class Solution {
public:
    bool evaluateTree(TreeNode* root) {
        if(root->left==nullptr)return root->val?true:false;

        bool left=evaluateTree(root->left);
        bool right=evaluateTree(root->right);
        
        return root->val==2?left|right:left&right;
    }
};

二、求根节点到叶节点数字之和

129. 求根节点到叶节点数字之和 - 力扣（LeetCode）

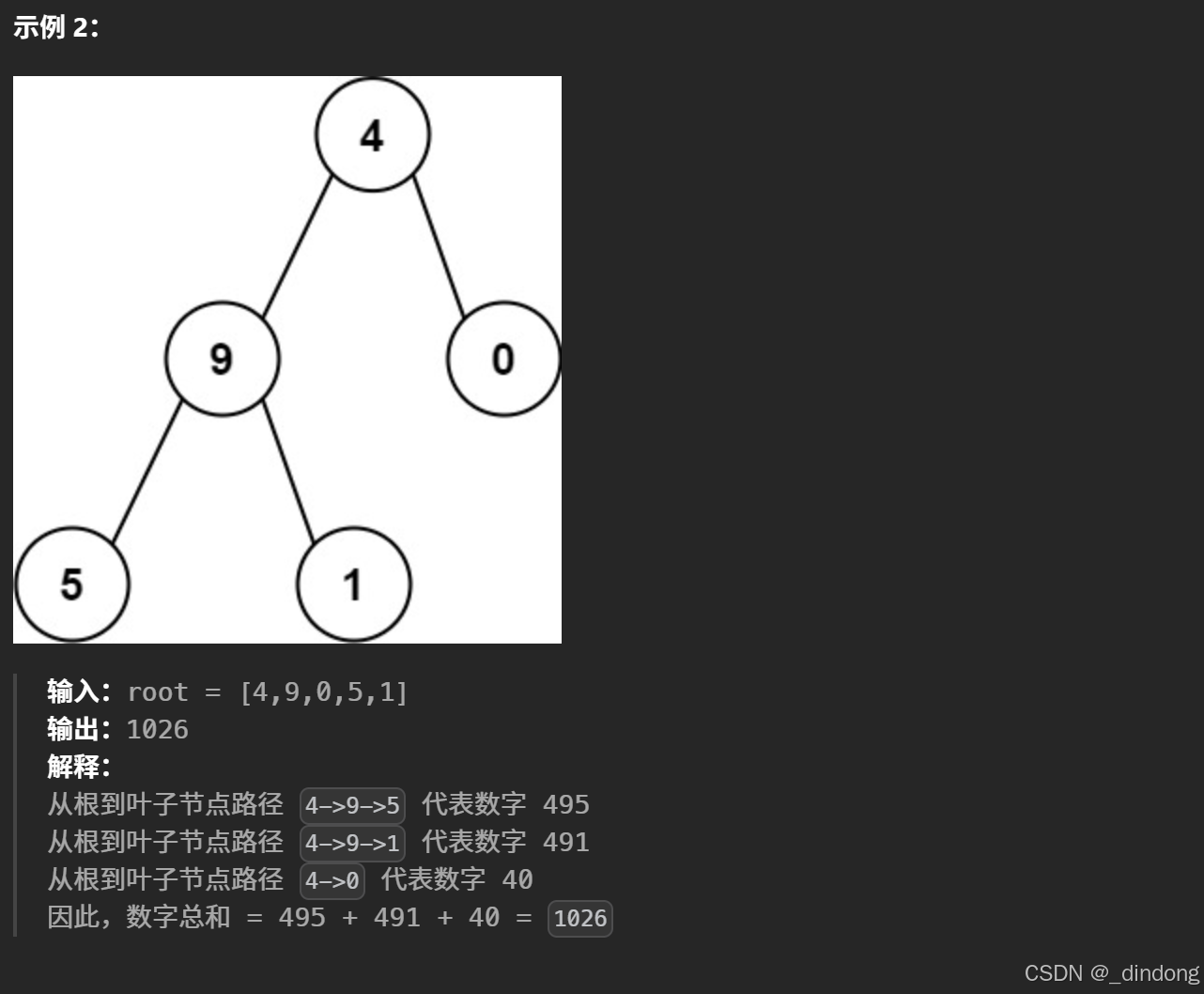
到达叶子节点返回总和

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        return dfs(root,0);
    }
    int dfs(TreeNode*root,int presum)
    {
        presum=presum*10+root->val;
        if(root->left==nullptr&&root->right==nullptr)return presum;
        int ret=0;
        if(root->left)ret+=dfs(root->left,presum);
        if(root->right)ret+=dfs(root->right,presum);
        return ret;
    }
};

三、二叉树剪枝

814. 二叉树剪枝 - 力扣（LeetCode）

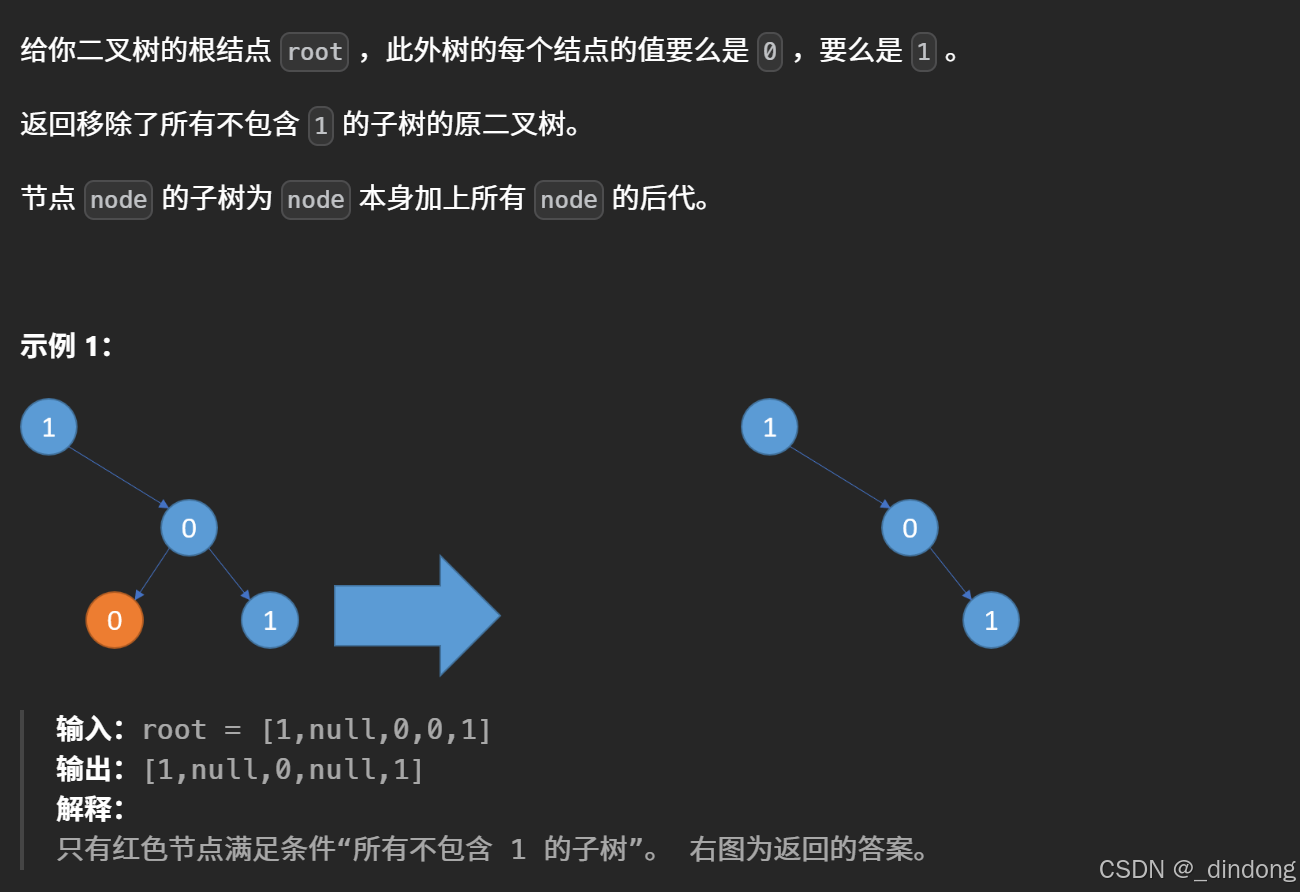
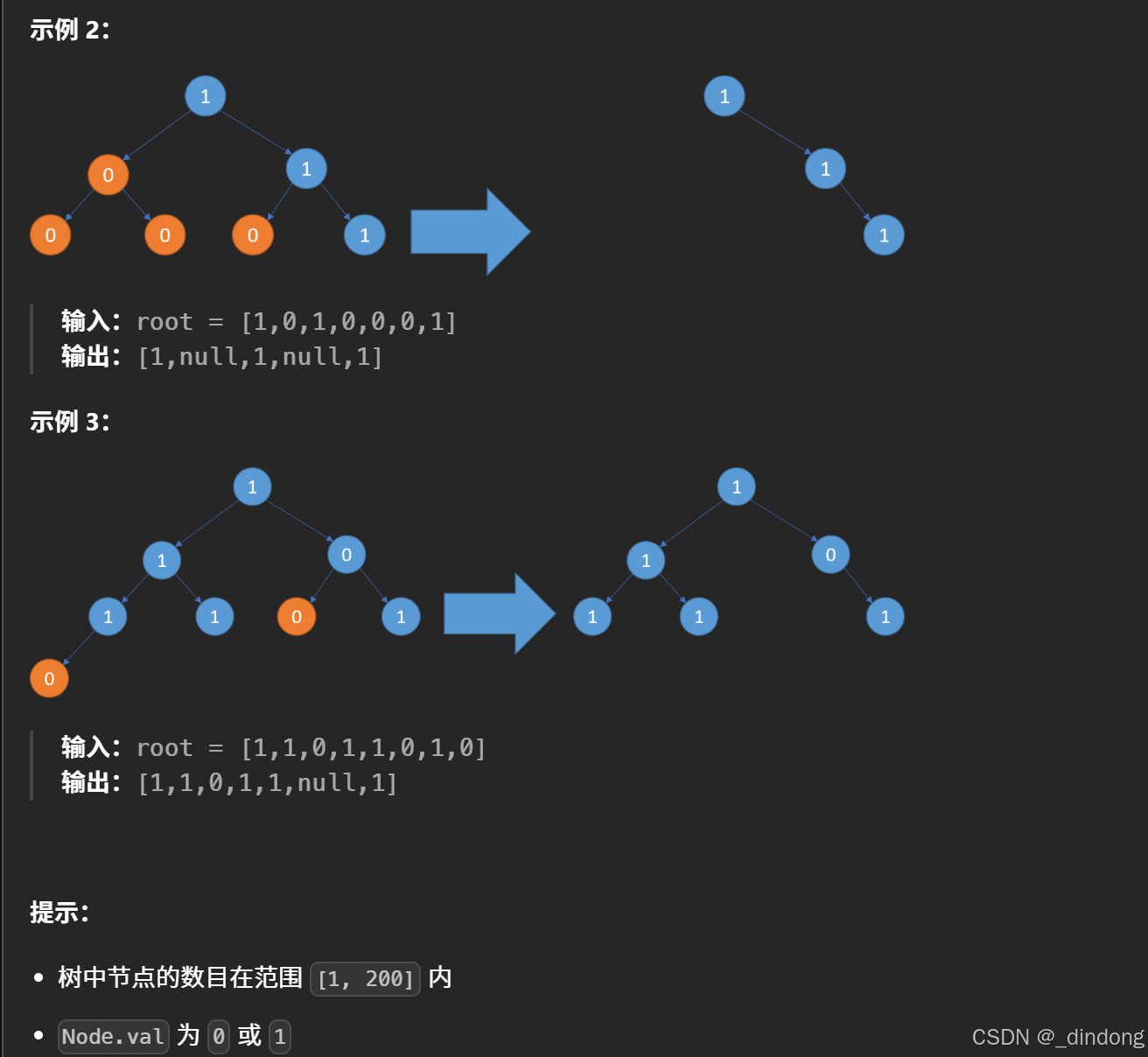
大多数剪枝就是做一个判断，不需要害怕它。

思路如下：判断剪枝，那我们得判断局部根节点以及它的左右子树是否都为零。如果是0让这个结点置空即可。递归终止条件就是遇到空返回·空·。

要有一个局部到整体的过程，递归我们肯定先递归到了最底，那么这时判断的肯定是叶子节点，叶子节点如果是0那么直接置为nullptr了，然后返回根，这样如果根节点左右子树全都是0，那么递归返回到这一步的时候，也可以用相同的判断条件进行置nullptr。

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if(root==nullptr)return nullptr;

        root->left=pruneTree(root->left);
        root->right=pruneTree(root->right);
        if(root->left==nullptr&&root->right==nullptr&&root->val==0)
        {
          //delete root;防止内存泄漏
          root=nullptr;
        }
        return root;
    }
};

四、验证二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）

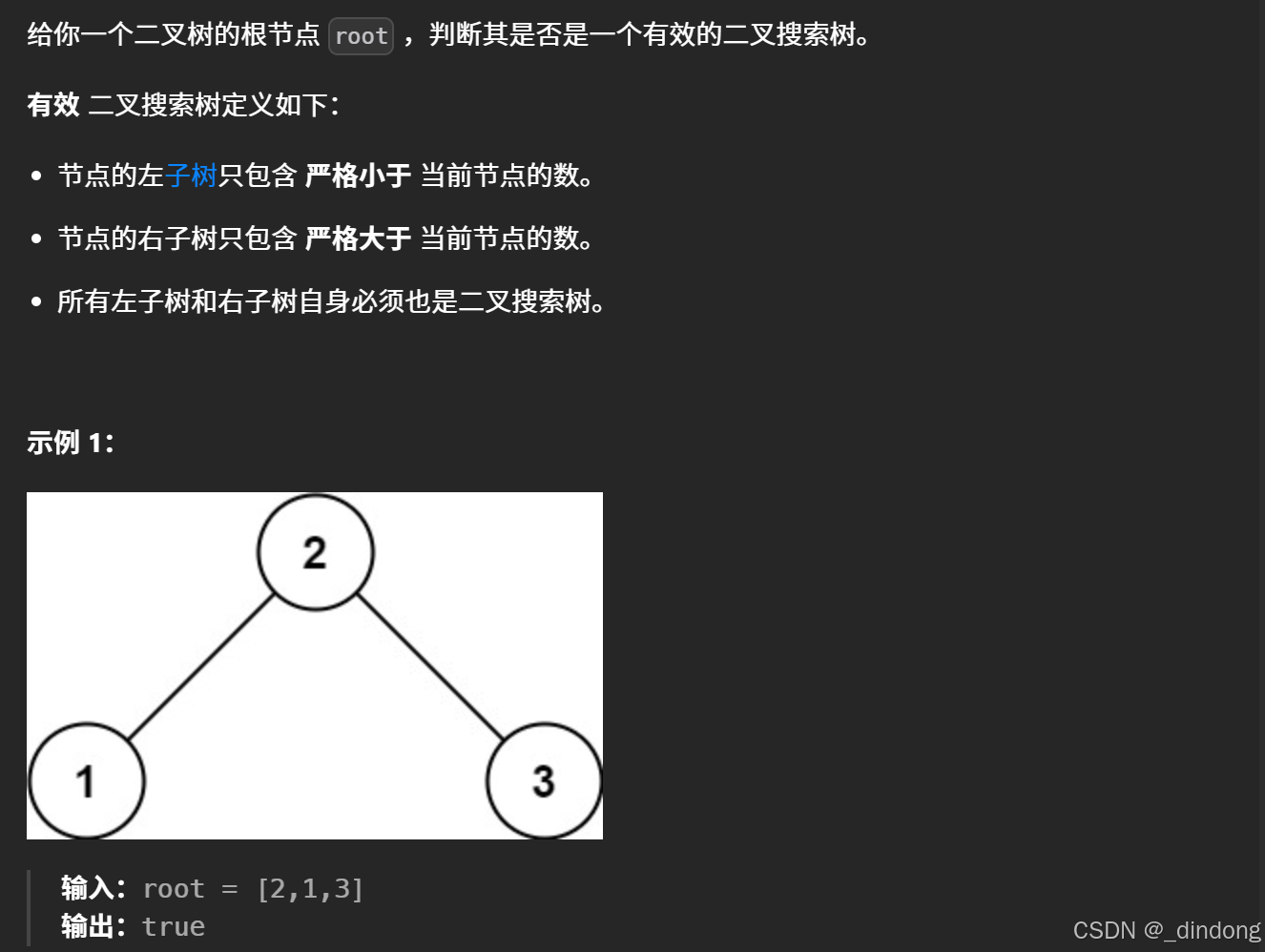
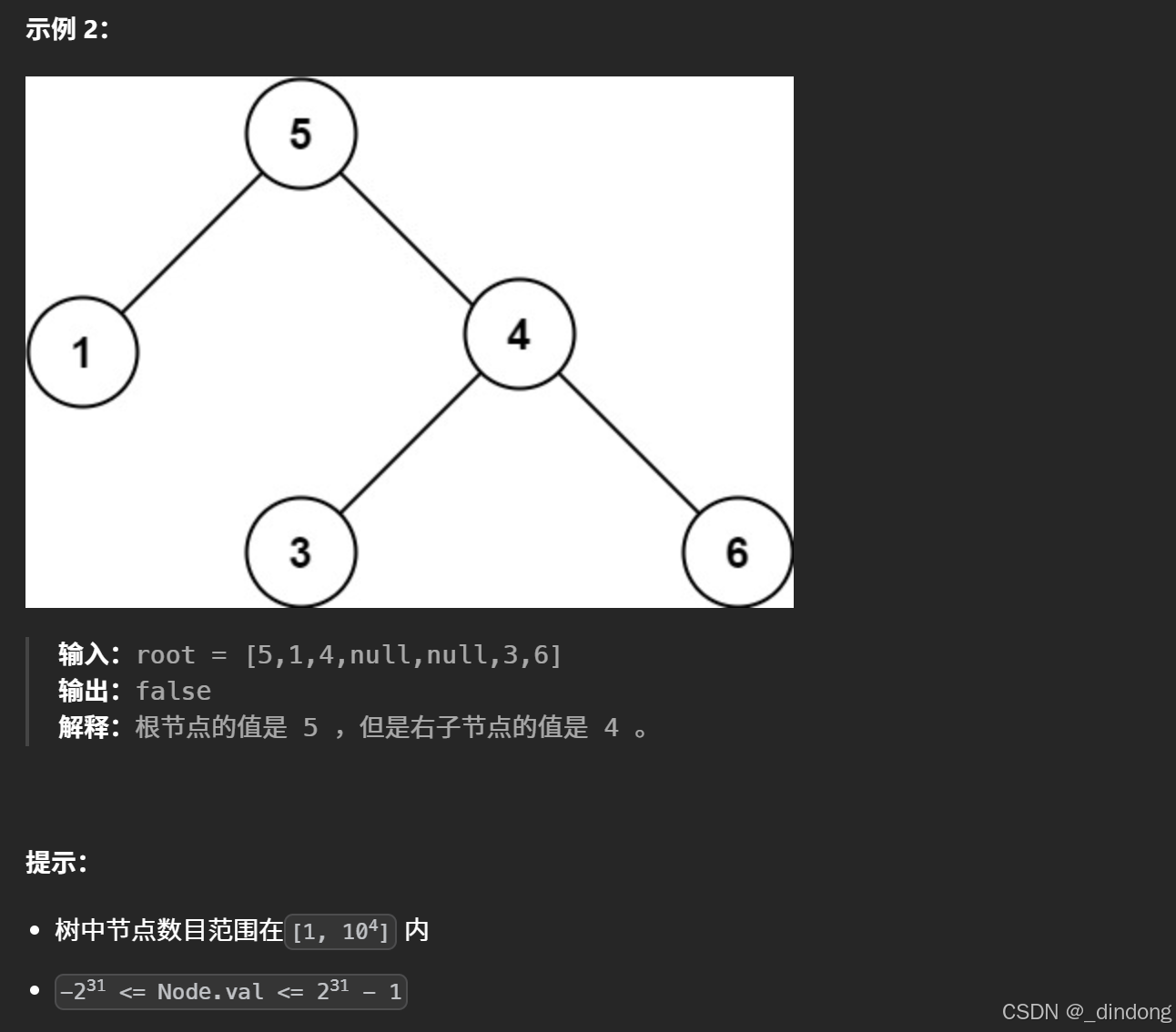
利用二叉搜索树中序遍历递增的特性+剪枝

利用二叉搜索树中序遍历有序的特性，可以设置一个全局变量prev初始化为负无穷，中序遍历，遍历到的节点->val，大于prev则更新prev，不大直接返回false。

此外我们还需要递归判断左右子树是不是二叉搜索树，因为是中序遍历，我们肯定在比较prev的时候先检查了左子树，这样，如果左子树是false就直接return false，提高了效率，右子树也是一样。

#include <climits>
class Solution {
public:
    //用例范围prev有int最小值，开一个更小的
    int prev=LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if(!root)return true;

        if(!isValidBST(root->left))return false;
        if(root->val<=prev)return false;
        prev=root->val;
        if(!isValidBST(root->right))return false;
        return true;
    }
};

五、二叉搜索树中第K小的元素

230. 二叉搜索树中第 K 小的元素 - 力扣（LeetCode）

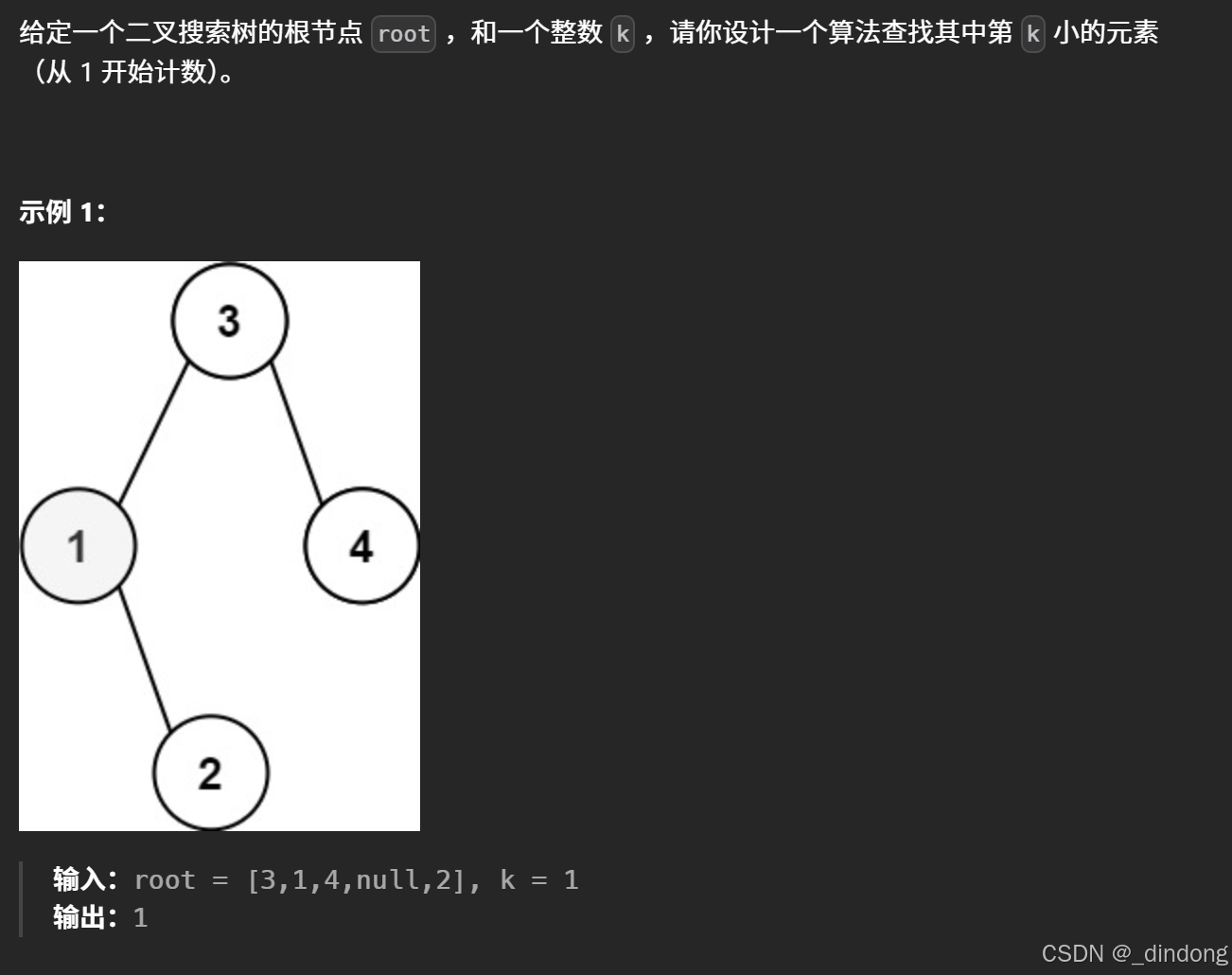
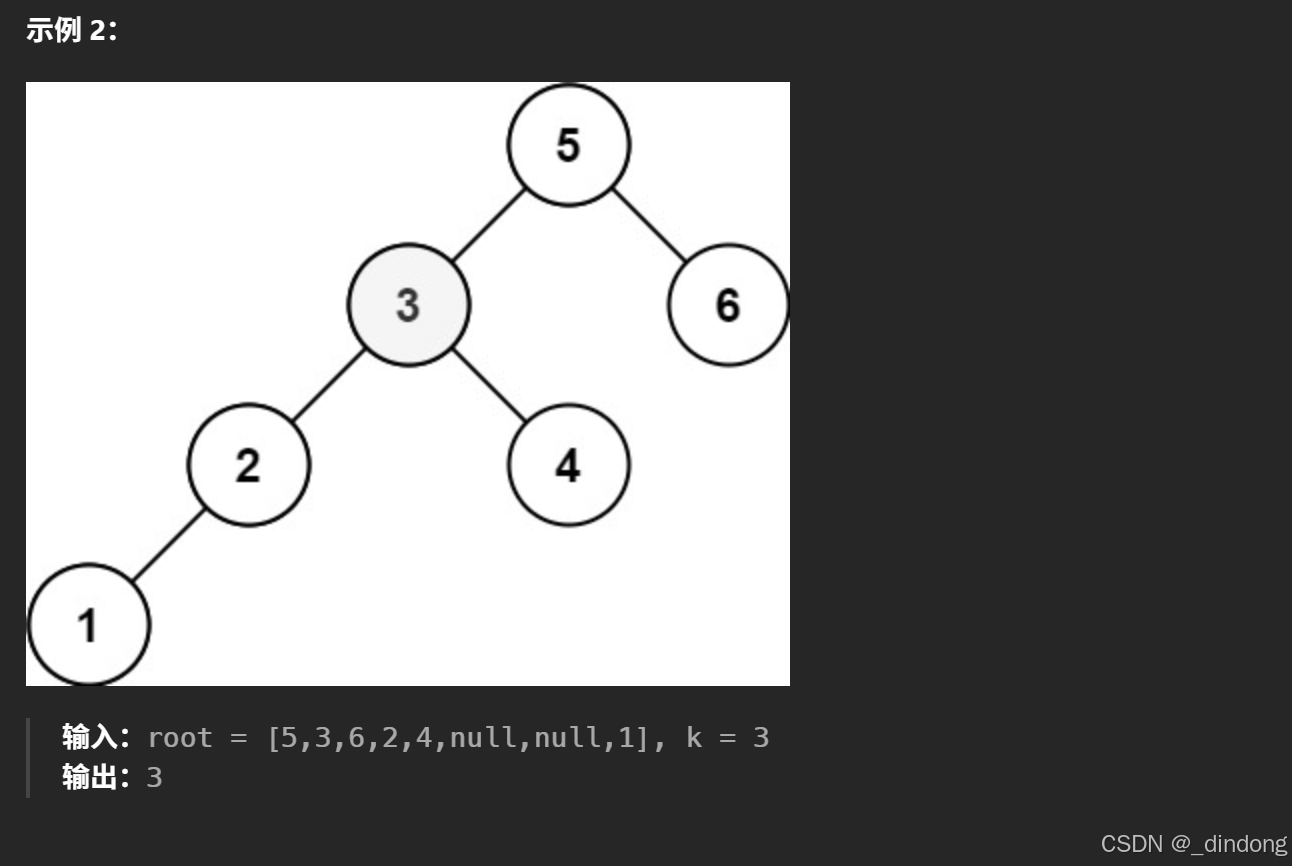
设置一个计数器，每次中序遍历的时候count==0时就更新

class Solution {
    //默认是0
    int ret,count;
public:
    int kthSmallest(TreeNode* root, int k) {
        count=k;
        dfs(root);
        return ret;
    }
    void dfs(TreeNode* root)
    {
        if(root==nullptr||count==0)return;
        dfs(root->left);
        if(--count==0)ret=root->val;
        dfs(root->right);
    }
};

六、二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode）

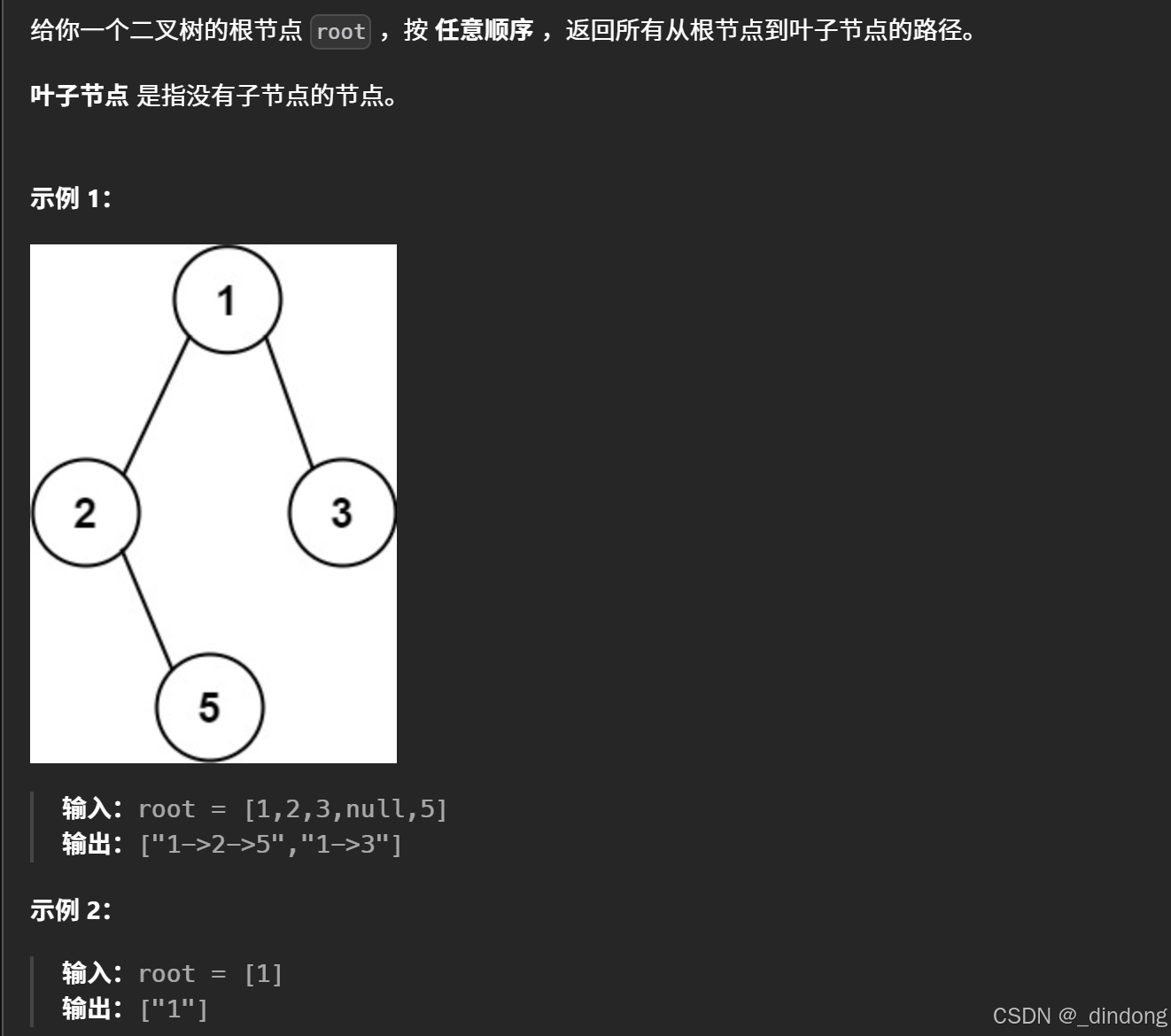
递归开始先push（先序遍历）如果此时是叶子节点就push_back路径

class Solution {
public:
    vector<string> ret;
    vector<string> binaryTreePaths(TreeNode* root) {
        string path;
        dfs(root,path);
        return ret;
    }
    //path不能传引用，不然还要实现回溯
    void dfs(TreeNode*root,string path)
    {
        path+=to_string(root->val);
        if(root->left==nullptr&&root->right==nullptr)
        {
            ret.push_back(path);
            return;
        }
        path+="->";
        if(root->left)dfs(root->left,path);
        if(root->right)dfs(root->right,path);
    }
};

此篇完。