【Leetcode】120. Triangle

最新推荐文章于 2024-06-27 13:46:32 发布

原创最新推荐文章于 2024-06-27 13:46:32 发布 · 317 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#Leetcode

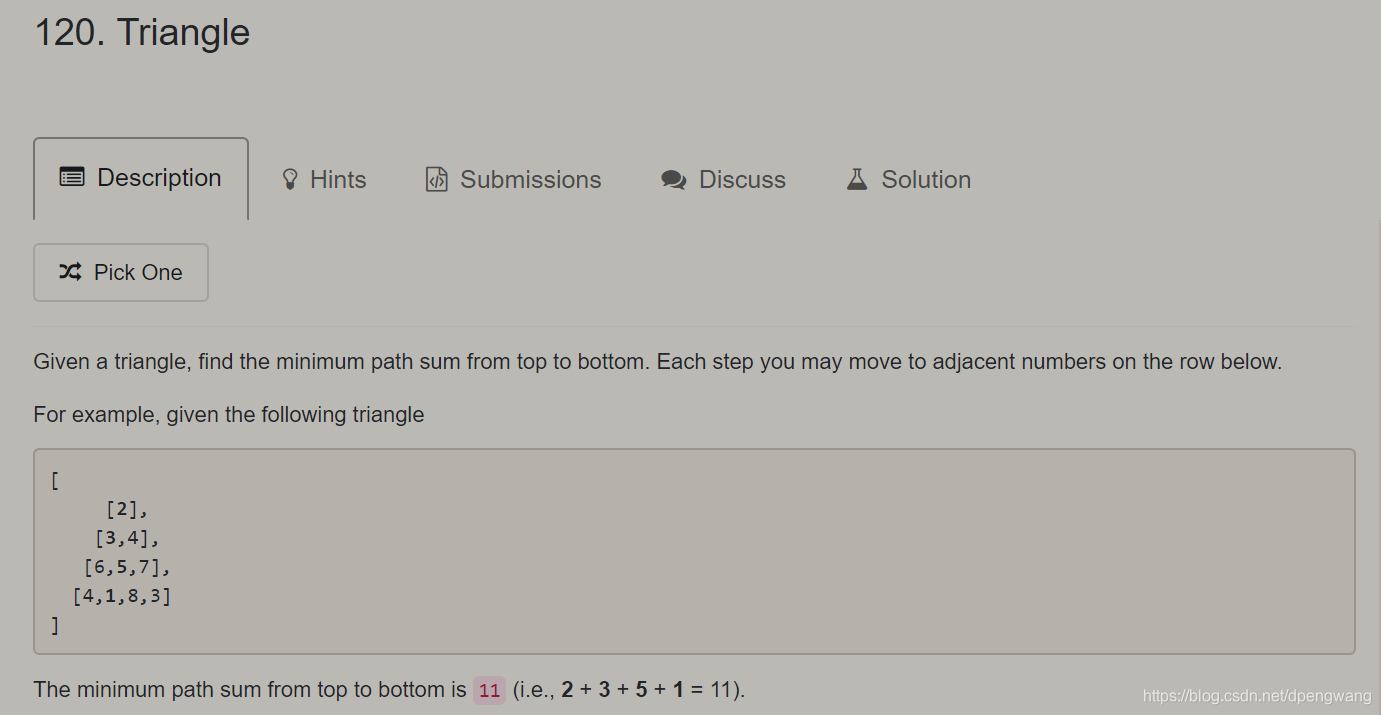
本文探讨了金字塔路径求和问题，通过动态规划和递归两种方法寻找从金字塔顶端到底端的最短路径和。动态规划采用自底向上策略，避免重复计算，提高效率；递归方法虽直观但耗时较长。文章提供了详细的算法解释及Python代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述求金字塔顶端到底端的最短和路径。

方法1 DP法

DP法。对于每个位置A，都对应这个上面两个点B和C，那么B和C都能到达A，我们肯定选择一条路径较短的。所以递推方法如下：

dp[i][j] = min(dp[i-1][j],dp[i-1][j-1]) + curr_val

因为路径和都是按行计算的，所以我们不必使用二维数组来记录dp值，用一位数组即可。
AC代码

class Solution:
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        res = [0 for i in range(len(triangle))]
        for i in range(len(triangle)):
            #
            if i == 0:
                res[0] = triangle[i][0]
                continue
            a =res[0]
            res[0] += triangle[i][0]
            for j in range(1,i):
                b = res[j]
                res[j] = min(a,res[j]) + triangle[i][j]
                a = b
            res[i] = a + triangle[i][i]

        # print(res)
        return min(res)

可以改进一下，这里不仅用了长度为n的一位数组，还用了两个额外的变量。因为我们从上往下，每次都会多出来一个元素，涉及到覆盖的问题。
如果我们从下往上的话，就不会出现这个问题，而且最终的结果就是一位数组的第一个元素。

class Solution3:
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        res = triangle[-1][:]
        for i in range(len(triangle)-2, -1, -1):
            for j in range(i+1):
                res[j] = min(res[j],res[j+1]) + triangle[i][j]
        return res[0]

方法2 递归法

这道题也可以用递归来解，对于每一个点，下一个目标点都有两个，相当于二叉树分裂成两个子节点，我们可以用递归法来找出所有的路径。这种方法虽然比方法1节省了存储空间（只需要存储当前点的坐标即可），但是非常耗时。

自顶向下的递归

class Solution2:
    """
    :type triangle: List[List[int]]
    :rtype: int
    """
    def minimumTotal(self, triangle):
        self.res = float("inf")
        self.DFS_fromTopToBottom(0, 0 , triangle, 0)
        return self.res

    def DFS_fromTopToBottom(self,i, j, triangle,curr_res):
        if i == len(triangle)-1 :
            self.res = min(triangle[i][j]+curr_res, self.res)
            return
        else:
            # print(i,j)
            self.DFS_fromTopToBottom(i + 1, j , triangle, curr_res + triangle[i][j])
            self.DFS_fromTopToBottom(i + 1, j+1, triangle, curr_res + triangle[i][j])

自底向上的递归

class Solution:
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        self.res = float("inf")
        for i in range(len(triangle)):
            self.DFS_fromBottomToTop(len(triangle)-1, i, triangle, 0)
        return self.res

    def DFS_fromBottomToTop(self,i, j, triangle,curr_res):
        if i == 0 :
            self.res = min(triangle[0][0]+curr_res, self.res)
            return
        if j ==0:
            self.DFS_fromBottomToTop(i-1, 0, triangle, curr_res + triangle[i][j])
        elif j == i:
            self.DFS_fromBottomToTop(i - 1, j-1, triangle, curr_res + triangle[i][j])
        else:
            # print(i,j)
            self.DFS_fromBottomToTop(i - 1, j - 1, triangle, curr_res + triangle[i][j])
            self.DFS_fromBottomToTop(i - 1, j, triangle, curr_res + triangle[i][j])