结合MTF的物理原理和代码实现,我们可以从数学推导和工程实现两个两个维度详细解析MTF计算算法。下面将按照“原理→代码映射→关键步骤解析”的逻辑展开说明。
一、MTF计算的核心原理回顾
MTF(调制传递函数)本质是成像系统对不同空间频率的正弦信号的对比度传递能力,其计算依赖于以下信号处理链:
边缘扩散函数(ESF) → 线扩散函数(LSF) → 空间频率响应(SFR) → MTF
- 边缘扩散函数(ESF):理想锐利边缘经过成像系统后会变得模糊,ESF描述了“边缘从暗到亮的灰度变化曲线”(空间域)。
- 线扩散函数(LSF):ESF的一阶导数,描述系统对一条无限细直线的扩散效果(点扩散函数PSF的线积分)。
- 空间频率响应(SFR):LSF的傅里叶变换,包含幅度(MTF)和相位(PTF)信息。
- MTF:SFR的幅度谱,归一化后得到“不同空间频率下的对比度传递效率”。
二、代码与原理的映射关系
以下是代码中核心函数与MTF计算步骤的对应关系,结合数学公式说明:
1. 生成测试边缘图像(模拟成像系统输入)
def generate_test_edge(width=512, height=512, edge_blur=2.0):
# 理想锐利边缘(左暗右亮)
edge_image = np.ones((height, width))
edge_position = width // 2
edge_image[:, :edge_position] = 0
# 高斯模糊模拟系统模糊(模拟实际成像的扩散)
blurred_edge = gaussian_filter(edge_image, sigma=edge_blur)
return blurred_edge
- 原理:实际中通过拍摄“锐利边缘靶标”获取ESF,代码用高斯模糊模拟镜头/传感器的扩散效应(σ越大,系统模糊越严重)。
- 物理意义:理想边缘是阶跃信号(从0到1的突变),经过系统后变为平滑过渡的模糊边缘,即ESF的原始数据。
2. 提取边缘扩散函数(ESF)
def extract_esf(edge_image, roi_size=100):
# 沿垂直方向平均,得到水平方向的亮度分布
edge_profile = np.mean(edge_image, axis=0)
# 找边缘位置(梯度最大处)
edge_gradient = np.abs(np.gradient(edge_profile))
edge_position = np.argmax(edge_gradient)
# 提取边缘区域并平均,得到ESF
esf_region = edge_image[:, start:end]
esf = np.mean(esf_region, axis=0) # 垂直方向平均降噪
# 归一化到[0,1]
esf = (esf - np.min(esf)) / (np.max(esf) - np.min(esf))
return esf, start, end
- 原理:ESF是“边缘过渡区的灰度分布”,需从图像中提取并降噪。
- 步骤1:对边缘图像沿垂直方向(边缘方向)取平均,得到1D灰度曲线(消除垂直方向噪声)。
- 步骤2:通过梯度找边缘中心(灰度变化最剧烈的位置),确定感兴趣区域(ROI)。
- 步骤3:对ROI再取平均,得到平滑的ESF曲线,并归一化到[0,1](暗区0,亮区1)。
- 数学表达:ESF(x) 描述位置x处的归一化灰度,理想ESF是阶跃函数,实际为平滑曲线。
3. 从ESF计算LSF(核心步骤)
# 代码中calculate_mtf函数的第一步
lsf = np.gradient(esf) # 对ESF求导得到LSF
- 原理:线扩散函数(LSF)是ESF的一阶导数,物理意义是“系统对一条细线的扩散效果”。
- 数学推导:理想阶跃边缘的导数是δ函数(无限窄),实际ESF的导数即为LSF,表示“单位长度内的灰度变化率”。
- 直观理解:ESF的斜率越大(过渡越陡),LSF越集中(峰值越高),说明系统对细节的还原能力越强。
4. 从LSF计算SFR和MTF(核心步骤)
def calculate_mtf(esf, pixel_size=1.0):
# 1. 求LSF
lsf = np.gradient(esf)
# 2. 傅里叶变换得到SFR
n = len(lsf)
lsf_fft = fft(lsf) # 快速傅里叶变换
sfr = fftshift(lsf_fft) # 移动零频到中心
# 3. 幅度谱归一化得到MTF
mtf = np.abs(sfr) # 取幅度(SFR的幅度分量)
mtf = mtf / mtf[int(n/2)] # 归一化(零频处MTF=1)
# 4. 计算空间频率(单位:线对/毫米)
frequencies = fftfreq(n, d=pixel_size) # 频率轴(周期/像素)
frequencies = fftshift(frequencies) # 对应SFR的频率移动
frequencies = frequencies[frequencies >= 0] # 只保留正频率
mtf = mtf[int(n/2):] # 只保留正频率的MTF
return frequencies, mtf
-
原理:傅里叶变换将空间域的LSF转换为频率域的SFR,MTF是SFR的幅度谱。
- 步骤1:FFT变换:将LSF(空间域)转换为SFR(频率域),SFR是复数(包含幅度和相位)。
- 步骤2:幅度提取:MTF = |SFR|,表示不同频率的信号幅度衰减比例。
- 步骤3:归一化:零频(直流分量)处的MTF定义为1(系统对均匀亮度的传递效率为100%)。
- 步骤4:频率计算:通过像素尺寸(d,单位毫米)将“周期/像素”转换为“线对/毫米”(1线对=2个像素周期)。
-
数学表达:
[
\text{SFR}(f) = \mathcal{F}{\text{LSF}(x)}, \quad \text{MTF}(f) = \left| \text{SFR}(f) \right| / \left| \text{SFR}(0) \right|
]
其中( \mathcal{F} )是傅里叶变换,( f )是空间频率(线对/毫米)。
5. 结果可视化
def plot_results(edge_image, esf, frequencies, mtf):
# 显示边缘图像、ESF曲线、MTF曲线
...
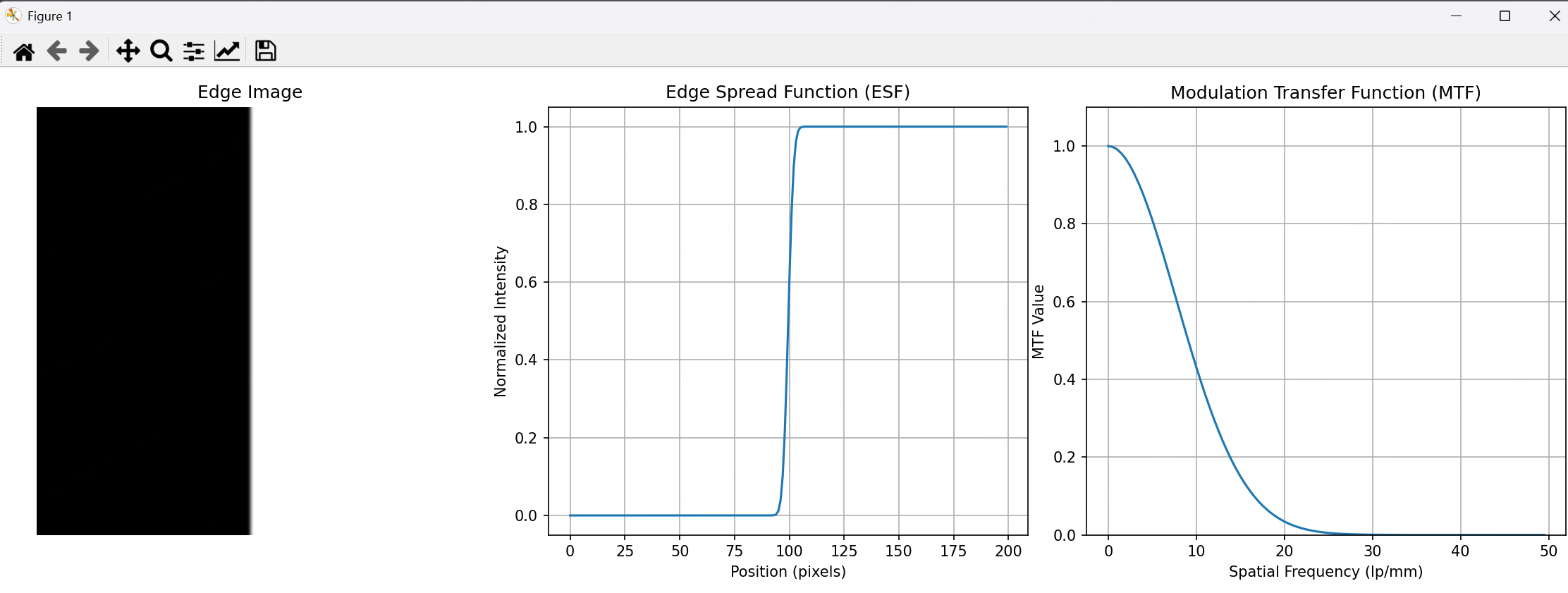
- 边缘图像:直观展示系统的模糊程度;
- ESF曲线:过渡越陡,说明系统边缘还原越好;
- MTF曲线:横轴为空间频率(高频=细节更精细),纵轴为传递效率。曲线下降越慢,系统分辨率越高。
三、关键逻辑与物理意义解析
-
为什么用边缘法计算MTF?
实际中难以生成理想的正弦光栅(MTF定义中的输入),而锐利边缘容易制作(如黑白交界的靶标)。通过边缘的扩散特性反推系统的频率响应,是工程上的实用方法。 -
MTF曲线的解读
- 低频段(如10线对/毫米):MTF值接近1,说明系统能很好传递大尺度细节的对比度;
- 高频段(如50线对/毫米):MTF值快速下降,当MTF≈0.1时,人眼已难以分辨细节,对应系统的极限分辨率。
-
代码中的参数影响
edge_blur:模拟系统模糊,σ越大,ESF过渡越平缓,LSF越分散,MTF曲线下降越快(高频传递能力差);pixel_size:像素越小(如0.001毫米),可计算的最高空间频率越高(频率上限=1/(2×pixel_size))。
总结
代码实现严格遵循MTF的物理定义:通过边缘扩散函数(ESF)提取系统的空间域响应,经导数(LSF)和傅里叶变换(SFR)转换到频率域,最终得到反映对比度传递能力的MTF。核心逻辑是“空间域→频率域”的转换,这也是所有成像系统分辨率评价的通用方法。实际应用中,只需将generate_test_edge替换为真实边缘图像的读取,即可计算实际系统的MTF。
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter
from scipy.fft import fft, fftshift, fftfreq
def generate_test_edge(width=512, height=512, edge_blur=2.0):
"""生成测试用的边缘图像,用于演示MTF计算"""
# 创建理想的锐利边缘
edge_image = np.ones((height, width))
edge_position = width // 2
edge_image[:, :edge_position] = 0 # 左侧为暗区,右侧为亮区
# 添加高斯模糊模拟实际成像系统的模糊
blurred_edge = gaussian_filter(edge_image, sigma=edge_blur)
return blurred_edge
def extract_esf(edge_image, roi_size=100):
"""从边缘图像中提取边缘扩散函数(ESF)"""
height, width = edge_image.shape
# 找到边缘位置(亮度变化最大的列)
edge_profile = np.mean(edge_image, axis=0) # 沿垂直方向平均得到水平方向的亮度分布
edge_gradient = np.abs(np.gradient(edge_profile))
edge_position = np.argmax(edge_gradient)
# 提取感兴趣区域(ROI),围绕边缘位置
start = max(0, edge_position - roi_size // 2)
end = min(width, edge_position + roi_size // 2)
# 提取边缘区域并沿垂直方向平均,得到ESF
esf_region = edge_image[:, start:end]
esf = np.mean(esf_region, axis=0) # 沿垂直方向平均
# 归一化ESF到[0, 1]范围
esf = (esf - np.min(esf)) / (np.max(esf) - np.min(esf))
return esf, start, end
def calculate_mtf(esf, pixel_size=1.0):
"""
从边缘扩散函数(ESF)计算调制传递函数(MTF)
参数:
esf: 边缘扩散函数
pixel_size: 像素尺寸(mm),用于计算实际空间频率
返回:
frequencies: 空间频率 (线对/毫米)
mtf: 调制传递函数值
"""
# 对ESF求导得到线扩散函数(LSF)
lsf = np.gradient(esf)
# 对LSF进行傅里叶变换得到SFR
n = len(lsf)
lsf_fft = fft(lsf)
sfr = fftshift(lsf_fft)
# 计算幅度谱并归一化得到MTF
mtf = np.abs(sfr)
mtf = mtf / mtf[int(n/2)] # 直流分量归一化到1
# 计算空间频率 (线对/毫米)
frequencies = fftfreq(n, d=pixel_size)
frequencies = fftshift(frequencies)
frequencies = frequencies[frequencies >= 0] # 只保留正频率
# 只保留正频率部分的MTF
mtf = mtf[int(n/2):]
return frequencies, mtf
def plot_results(edge_image, esf, frequencies, mtf):
"""可视化结果:边缘图像、ESF和MTF曲线"""
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 显示边缘图像
axes[0].imshow(edge_image, cmap='gray')
axes[0].set_title('Edge Image')
axes[0].axis('off')
# 显示边缘扩散函数(ESF)
axes[1].plot(esf)
axes[1].set_title('Edge Spread Function (ESF)')
axes[1].set_xlabel('Position (pixels)')
axes[1].set_ylabel('Normalized Intensity')
axes[1].grid(True)
# 显示MTF曲线
axes[2].plot(frequencies, mtf)
axes[2].set_title('Modulation Transfer Function (MTF)')
axes[2].set_xlabel('Spatial Frequency (lp/mm)')
axes[2].set_ylabel('MTF Value')
axes[2].set_ylim(0, 1.1)
axes[2].grid(True)
plt.tight_layout()
plt.show()
def main():
# 生成测试边缘图像
edge_image = generate_test_edge(width=512, height=512, edge_blur=2.0)
# 提取边缘扩散函数
esf, _, _ = extract_esf(edge_image, roi_size=200)
# 计算MTF,假设像素尺寸为0.01毫米
frequencies, mtf = calculate_mtf(esf, pixel_size=0.01)
# 显示结果
plot_results(edge_image, esf, frequencies, mtf)
# 打印一些关键频率的MTF值
key_frequencies = [10, 20, 30, 40, 50]
print("关键频率的MTF值:")
for freq in key_frequencies:
idx = np.argmin(np.abs(frequencies - freq))
if idx < len(mtf):
print(f"{freq} lp/mm: {mtf[idx]:.4f}")
if __name__ == "__main__":
main()





















 1428
1428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








