【论文翻译】NSTformer:线性注意力在时空预测中已经足够

题目	Linear Attention is Enough in Spatial-Temporal Forecasting
论文链接	https://arxiv.org/abs/2408.09158
源码	https://github.com/XinyuNing/STformer-and-NSTformer
关键词	时空预测，Transformer，自注意力机制，线性复杂度，交通预测

摘要：

作为时空预测任务中最具代表性的场景，交通预测任务因其在空间和时间维度上复杂的关联性，吸引了机器学习领域的广泛关注。现有方法通常将道路网络随时间变化建模为时空图，分别处理空间和时间表示。然而，这些方法在捕捉道路网络的动态拓扑时面临困难，遇到了消息传递机制和过度平滑的问题，并且在分别学习空间和时间关系时面临挑战。为了解决这些局限性，我们提出将道路网络中不同时间步的节点作为独立的时空标记，输入到一个标准的Transformer中，以学习复杂的时空模式，并设计了STformer模型，达到了SOTA（当前最优）的效果。由于其二次复杂度，我们基于Nyström方法引入了NSTformer，以线性复杂度近似自注意力机制，但在某些情况下性能甚至略微优于STformer。对交通数据集的广泛实验结果表明，所提出的方法以较低的计算成本实现了最先进的性能。

NSTformer

1 引言
2 相关工作
- 2.1 交通预测中的Transformer
- 2.2 高效Transformer
3 问题设定
4 架构
5 实验
6 结论

1 引言

学习空间和时间表示是机器学习领域长期以来的愿景。实际上，卷积神经网络（CNN）通过利用空间信息的冗余来处理空间维度，而递归神经网络（RNN）则通过在神经元之间的递归结构来模拟时间的单向性。

交通预测因其在空间和时间维度上的复杂关联性以及广泛的应用，吸引了大量研究者的关注。大多数工作将交通道路网络建模为一个图，其中节点代表记录交通状况的传感器，边缘则表示节点之间的拓扑关系，如道路或距离。此外，某一时间段内的交通流量可以被看作是一个时空图。交通预测的目标是学习过去的交通流量如何映射到未来的交通流量。

在空间维度上，CNN被用来捕捉空间依赖性。由于CNN本能地处理网格数据而非拓扑数据，图卷积网络（GCN）被引入用于学习空间表示。然而，固定的静态图并不能代表不断变化的道路网络，为此动态图卷积被提出以缓解这一问题。尽管如此，图神经网络（GNN）仍然面临过度平滑的问题，并且相邻节点间的消息传递机制导致网络需要更深的层次来连接远程节点，这使得网络的参数难以优化。

在时间维度上，RNN和LSTM分别被用来捕捉时间依赖性。得益于并行处理和捕捉长程依赖的优势，Transformer已经成为不仅在自然语言处理，还在计算机视觉、序列决策等领域的事实标准。

在交通预测任务中，基于注意力的模型被提出，分别使用空间注意力和时间注意力来捕捉空间和时间维度的特征。也有工作仅使用Transformer来捕捉时间的连续性和周期性。

基本上，所有这些工作都基于时空图框架，然而这种框架存在以下几个固有缺陷：

即使使用动态GNN，仍然很难捕捉复杂且不断变化的道路网络中的空间依赖性和拓扑关系，固定的静态图更是如此。
GNN容易遇到过度平滑的问题，并且相邻节点之间的消息传递机制导致神经网络需要更多层次来连接远程节点，从而增加了训练和优化参数的难度，在大规模道路网络中尤其如此。
空间和时间表示分别学习需要更多的神经网络层数来捕捉跨空间和时间的依赖性。

受Transformer在图表示和时间预测上的突破启发，我们仅使用自注意力机制来研究交通预测，舍弃了任何图、卷积和递归模块。显然，我们可以立即克服由GNN引起的前两个问题。

首先，我们设计了一个名为STformer的模型（时空Transformer），在该模型中，我们将道路网络中的传感器在每个时间步作为独立的标记，而不是图中的节点。我们称这种标记为ST-Token，因为每个标记由时间步和空间位置唯一确定。接下来，由一段时间内的这些标记组成的序列被输入到标准Transformer中。虽然STformer是一个极其简洁的模型，但由于它能够捕捉跨时空的依赖性，它可以动态有效地学习时空表示，并在两个最常用的公共数据集METR-LA和PEMS-BAY上实现了最先进的性能。

由于自注意力的二次复杂度，STformer的计算成本在大规模道路网络或长期预测下是难以承受的，而其性能也可能受到限制。受Nyströmformer的启发，我们基于Nyström方法设计了NSTformer（Nyström时空Transformer），具有线性复杂度。令我们惊讶的是，NSTformer的性能略微超过了STformer。实际上，这一现象提出了一个开放问题，即近似注意力是否有其他正面效应，例如正则化。

我们的贡献总结如下：

我们研究了纯自注意力机制在时空预测中的表现。我们的STformer在METR-LA和PEMS-BAY数据集上达到了最先进的性能，并提供了一种全新且极其简洁的时空预测视角。
我们设计了NSTformer，具有O(N)复杂度，可以在最先进的性能下实现线性复杂度的时空预测。

2 相关工作

2.1 交通预测中的Transformer

我们已经在引言中讨论了深度学习在交通预测任务中的应用，特别是神经网络在学习时空表示方面的演变，并分析了其背后的原因。这里我们重点讨论Transformer在交通预测中的应用。

Guo等人提出了一种基于注意力的模型，设计了一个ST模块，将多个模块堆叠形成序列。在每个模块中，空间注意力和时间注意力分别并行学习空间表示和时间表示。随后，通过GCN和CNN进行进一步学习。Xu等人交替设置了空间Transformer和时间Transformer进行学习，同时在每个空间Transformer中并行结合GCN以捕捉空间依赖性。Zheng等人通过门控融合机制结合了空间和时间注意力机制。总结来看，这些工作仍然基于时空图框架，并且分别学习了空间表示和时间表示。

Jiang等人没有使用任何图结构，而是设计了复杂的语义空间注意力、地理空间注意力以及延迟感知特征变换来捕捉空间依赖性，同时并行使用了时间自注意力。

Liu等人的工作与我们的最为相关。他们提出了时空自适应嵌入，使得使用普通Transformer能够取得显著效果，而不是通过设计复杂的网络结构来获得微小的性能提升。然而，这仍然是分别学习空间表示和时间表示。虽然我们的模型简单有效，但通过同时学习真实的时空表示，我们已经克服了这个问题，从而使我们的工作以更低的计算成本超越了他们的性能。

2.2 高效Transformer

Transformer已经成为许多应用中的事实标准。然而，其核心模块——自注意力机制的空间和时间复杂度为 $O(N^2)$ ，这限制了其在大规模输入场景中的性能甚至可行性。研究界早已认识到这个问题，许多工作涌现出来以加速自注意力的计算。

Reformer、Big Bird、Linformer、Longformer、Routing Transformers等通过混合哈希、稀疏化或低秩近似方法加速了注意力分数的计算。Nyströmformer和一些其他方法通过使用核近似替代基于softmax的注意力来加速计算。Performer、Slim、RFA等使用随机投影来近似注意力计算。SOFT和Skyformer建议用快速评估的高斯核替代softmax操作。

其中，Nyströmformer实现了O(N)的复杂度。我们选择Nyströmformer作为NSTformer的基础，利用其他次二次复杂度的Transformer也是未来研究的有趣方向。

3 问题设定

我们在此正式定义交通预测任务。

定义 1（道路网络）：给定道路网络，其中有 $N$ 个传感器用于捕捉交通状况，如速度。在时间步 $t$ ，交通状况形成一个张量 $X_t \in \mathbb{R}^{N \times D}$ ，其中 $D$ 是特征维度，通常在交通速度预测任务中 $D = 1$ 。

请注意，在时空图框架下，路网表示为 $(\mathcal{V}, \mathcal{E}, A)$ ，其中 $\mathcal{V} = \{v_1, ..., v_N\}$ 表示节点， $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$ 表示边， $A$ 是邻接矩阵。在本研究中，我们的模型不使用任何图结构，也不对道路网络建模的图进行任何假设。

定义 2（交通流量）：在一段时间 $T$ 内，道路网络形成交通流量张量 $(X_1, X_2, ..., X_T) \in \mathbb{R}^{T \times N \times D}$ 。

定义 3（交通预测）：作为机器学习的本质，交通预测的学习方法是从假设类 $\mathcal{H}$ 中学习一个假设 $f$ ，该学习方法的目标是通过神经网络从过去 $T$ 个时间步的交通流量映射到未来 $T^{'}$ 个时间步的交通流量，如下所示：
$[X_{t-T+1}, ..., X_t] \xrightarrow{f} [X_{t+1}, ..., X_{t+T'}]$

相应地，时空图框架下的学习方式如下：

$[X_{t-T+1}, ..., X_t; G] \xrightarrow{f} [X_{t+1}, ..., X_{t+T'}]$

4 架构

4.1 流程

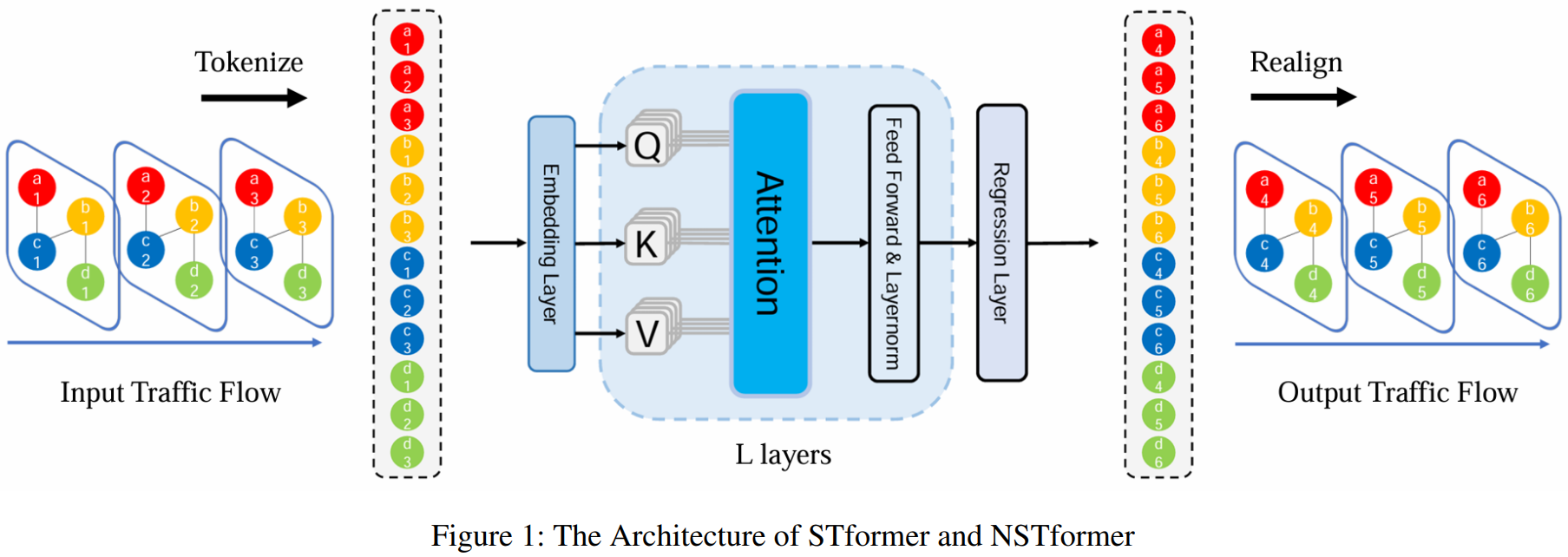
我们展示了我们的流程和模型架构，如图1所示。没有任何复杂的模块或数据处理，我们专注于如何捕捉复杂的时空关系。具体来说，我们不将交通流视为时空图，而是将其视为普通的3D张量，并将其展平为1D序列，然后输入到Transformer或其变体中。

通过这种方式，我们可以有效地捕捉每对ST-Token之间的关系。相应地，STformer的复杂度为 $O(N^2 T^2)$ ，当输入数据过大时是难以接受的。为了解决这一问题，我们设计了具有 $O (NT)$ 复杂度的NSTformer，生成了一个高效的模型。NSTformer与STformer的唯一区别在于注意力机制，前者使用的是线性Nyström注意力，而后者使用的是二次复杂度的自注意力。

4.2 嵌入层和回归层

如图1所示，我们的模型非常简洁，只有嵌入层、注意力机制和回归层。STformer和NSTformer的唯一区别是它们的注意力机制。我们首先介绍它们的公共模块，即嵌入层和回归层，然后详细介绍模型。

我们遵循了Liu等人的嵌入层设置，他们提出了时空自适应嵌入 $E_a$ ，用于捕捉复杂的时空依赖性，而不是使用图嵌入。

给定交通流 $\in \mathbb{R}^{T \times N \times D}$ ，其中 $T$ 表示输入的时间步长， $N$ 表示道路网络中传感器的数量，主流特征维度的设置为 $D = 3$ ，它包含了如速度、星期几时间标记（1至7）以及当天时间标记（1至288）。我们将这些特征嵌入为 $E_f \in \mathbb{R}^{T \times N \times 3 d_f}$ ，其中 $d_f$ 是特征嵌入的维度。然后通过一个简单而有效的嵌入 $E_a \in \mathbb{R}^{T \times N \times d_a}$ 来捕捉复杂的时空依赖关系。经过嵌入后，交通流被表示为 $\in \mathbb{R}^{T \times N \times d_h}$ ，其中 $d_h = 3 d_f + d_a$