实验室任务五

实验室第五周任务

一、python调库实现base64加解密

1.什么是Base64

Base64是一种基于64个可打印字符来表示二进制数据的表示方法。由于2^6=64，所以每6个比特为一个单元，对应某个可打印字符。

3个字节有24个比特，对应于4个Base64单元，即3个字节可由4个可打印字符来表示。在Base64中的可打印字符包括字母A-Z、a-z、数字0-9，这样共有62个字符，此外两个可打印符号在不同的系统中而不同。

2.python中的Base64模块

Base64模块真正用得上的方法只有8个，分别是：

encode, decode为一组, 专门用来编码和解码文件的, 也可以对StringIO里的数据做编解码；

encodestring, decodestring为一组，专门用来编码和解码字符串

b64encode, b64decode为一组, 用来编码和解码字符串，并且有一个替换符号字符的功能

因为Base64编码后的字符除了英文字母和数字外还有三个字符’ + / =‘,其中’=‘只是为了补全编码后的字符数为4的整数，而’+‘和’/‘在一些情况下需要被替换的，b64encode和b64decode正是提供了这样的功能。至于什么情况下’+‘和’/'需要被替换，最常见的就是对url进行Base64编码的时候。

urlsafe_b64decode, urlsafe_b64encode为一组，这个就是用来专门对url进行Base64编解码的，实际上也是调用的前一组函数。

base64.b64encode()将bytes类型数据进行base64编码，返回编码后的bytes类型

base64.b64deocde()将base64编码的bytes类型进行解码，返回解码后的bytes类型

decode的作用是将其他编码的字符串转换成unicode编码

encode的作用是将unicode编码转换成其他编码的字符串

3.python代码实现：

加密：加密函数base64.b64encode()可以将任何二进制数据编码为Base64字符串。例如，将字符串“hello world”编码为Base64：

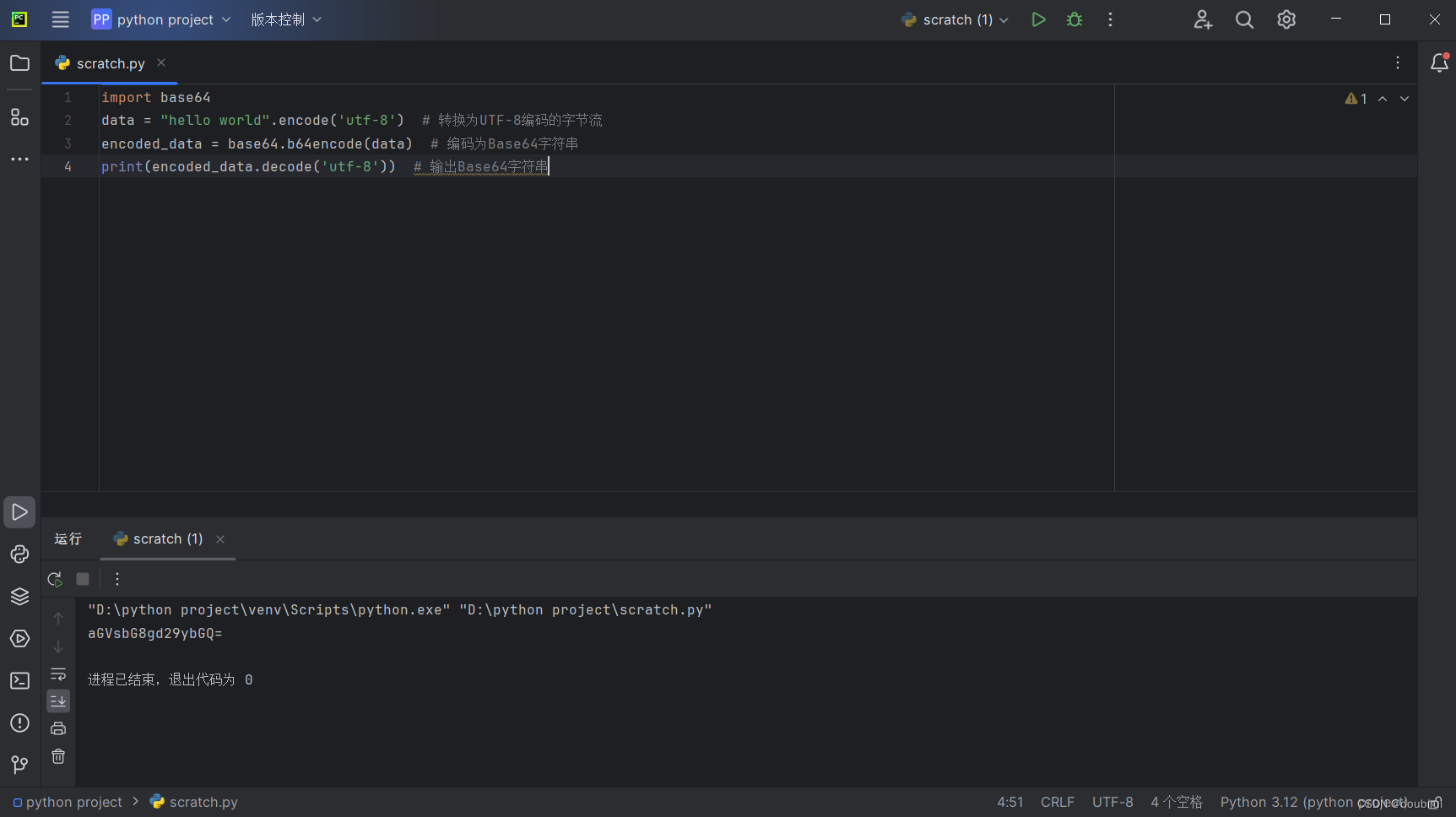
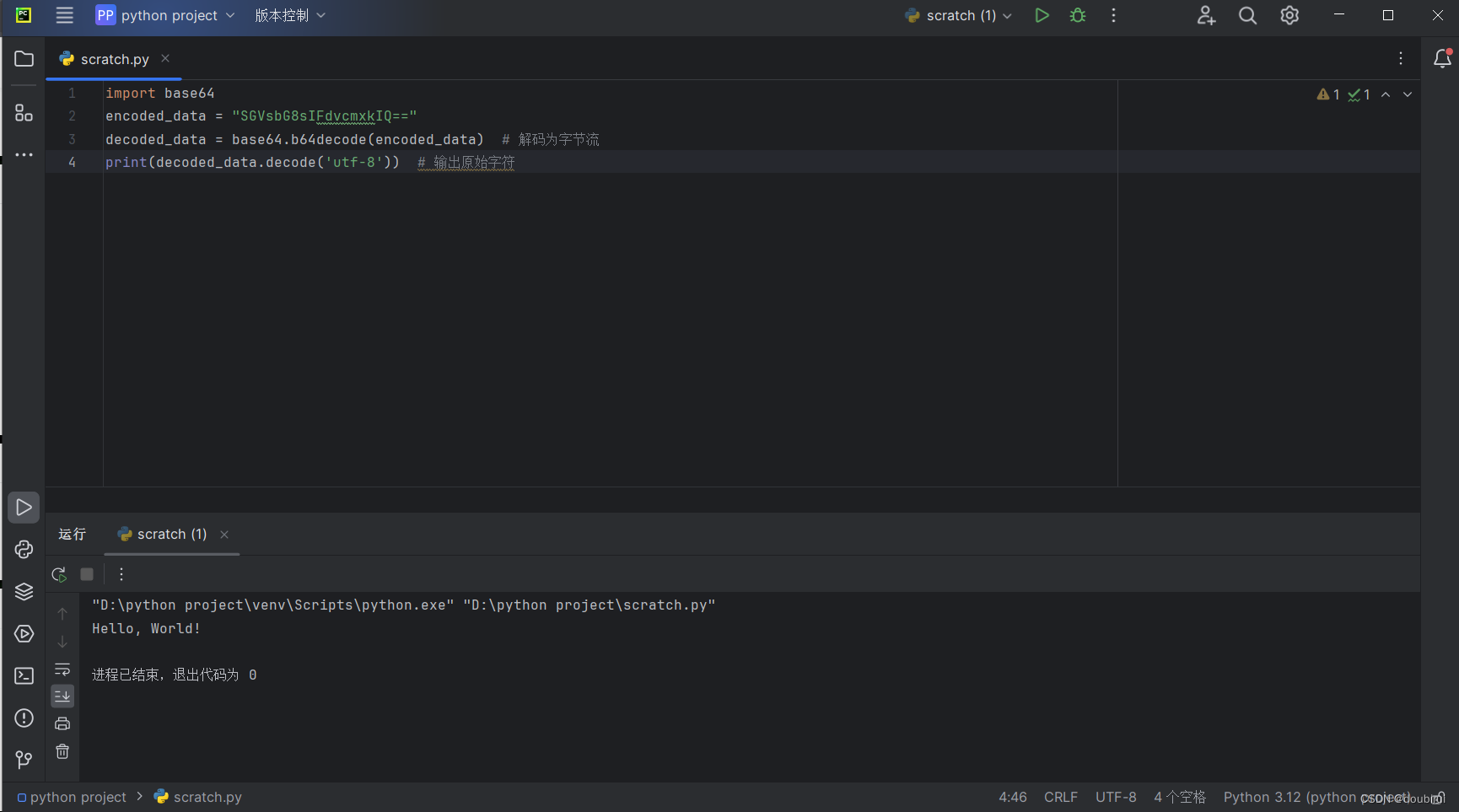
解码：解密函数base64.b64deode()可以将Base64字符串解码为原始二进制数据。例如，将Base64字符串“SGVsbG8sIFdvcmxkIQ==”解码为原始数据：

二、ctfshow-crypto

1）crypto0(凯撒)

这关很简单，只要将所给密码倒过来就是所求的flag

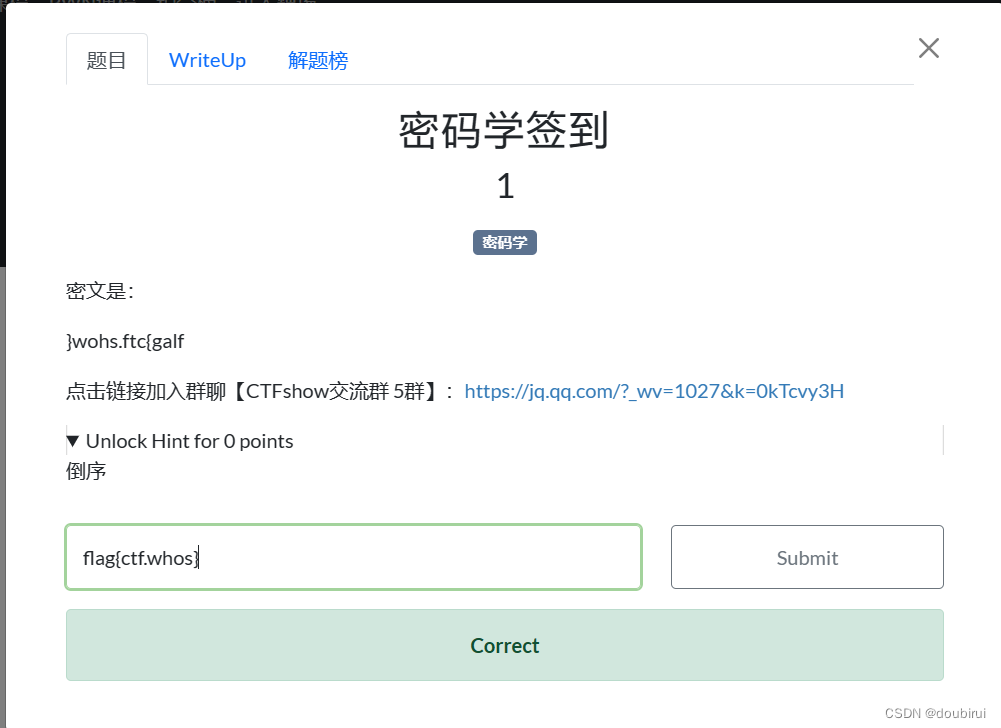
2）crypto2(jsfuck)

jsfuck知识点：

jsfuck源于一门编程语言brainfuck，其主要的思想就是只使用8种特定的符号来编写代码。而jsfuck也是沿用了这个思想，它仅仅使用6种符号来编写代码。它们分别是(、)、+、[、]、!。

基本转换：

false => ![]

true => !![]

undefined => ]

NaN => +[![]]

0 => +[]

1 => +!+[]

2 => !+[]+!+[]

10 => [+!+[]]+[+[]]

Array => []

Number => +[]

String => []+[]

Boolean => ![]

Function => [] ["filter"]

eval => [] ["filter"] ["constructor"] ( CODE )()

window => [] ["filter"] ["constructor"] ("return this")()

解题过程：

将所给密码复制粘贴到控制台上，回车后便可得到所求flag

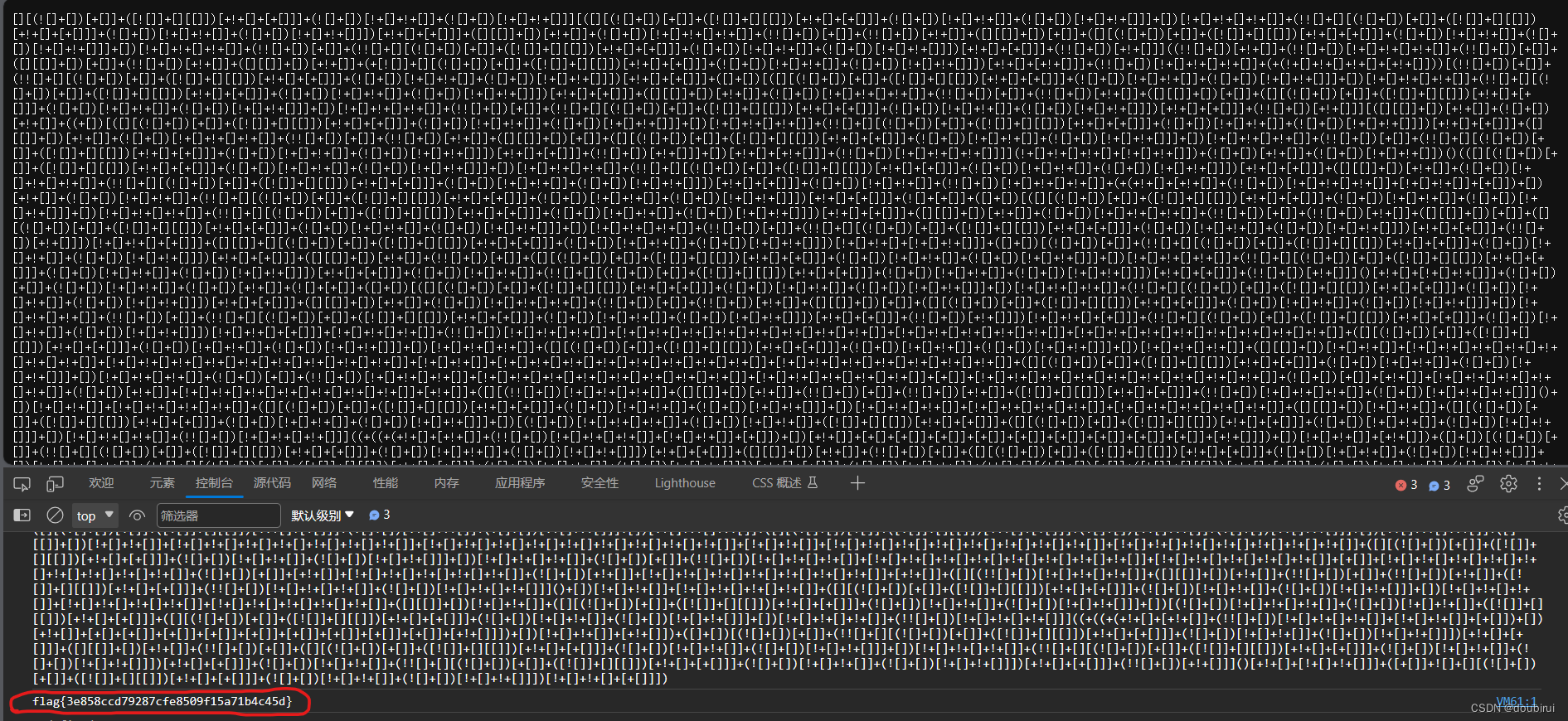
3）crypto3(aaencode)

aaencode:

aaencode是一种JavaScript的代码混淆/压缩工具，它可以将JavaScript代码转化为一个字符串，这个字符串看起来像是一堆乱码，但实际上包含了原始代码的所有功能。 （aaencode也被称为颜文字解密）

accencode解码方法：

1.直接通过在线解密

2.通过浏览器开发者工具将加密代码进行解密（只能解码不能加密）

3.通过浏览器开发者工具将加密代码进行解密

解题过程：

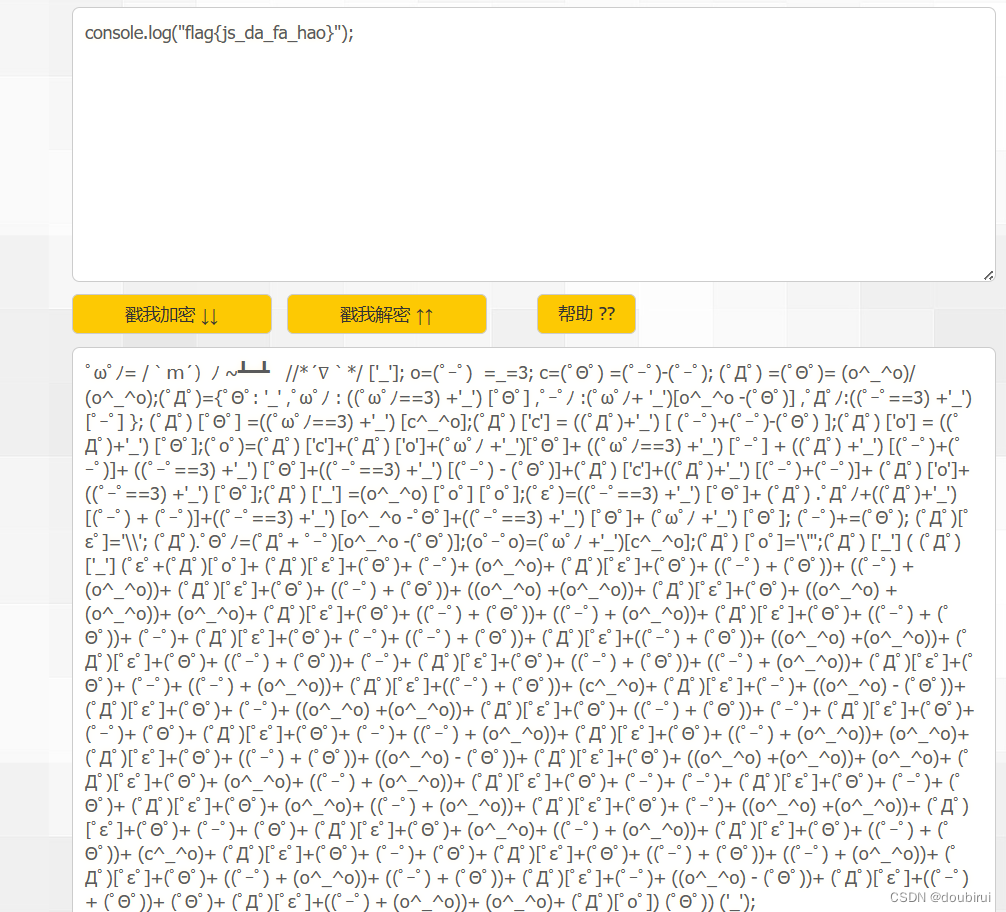
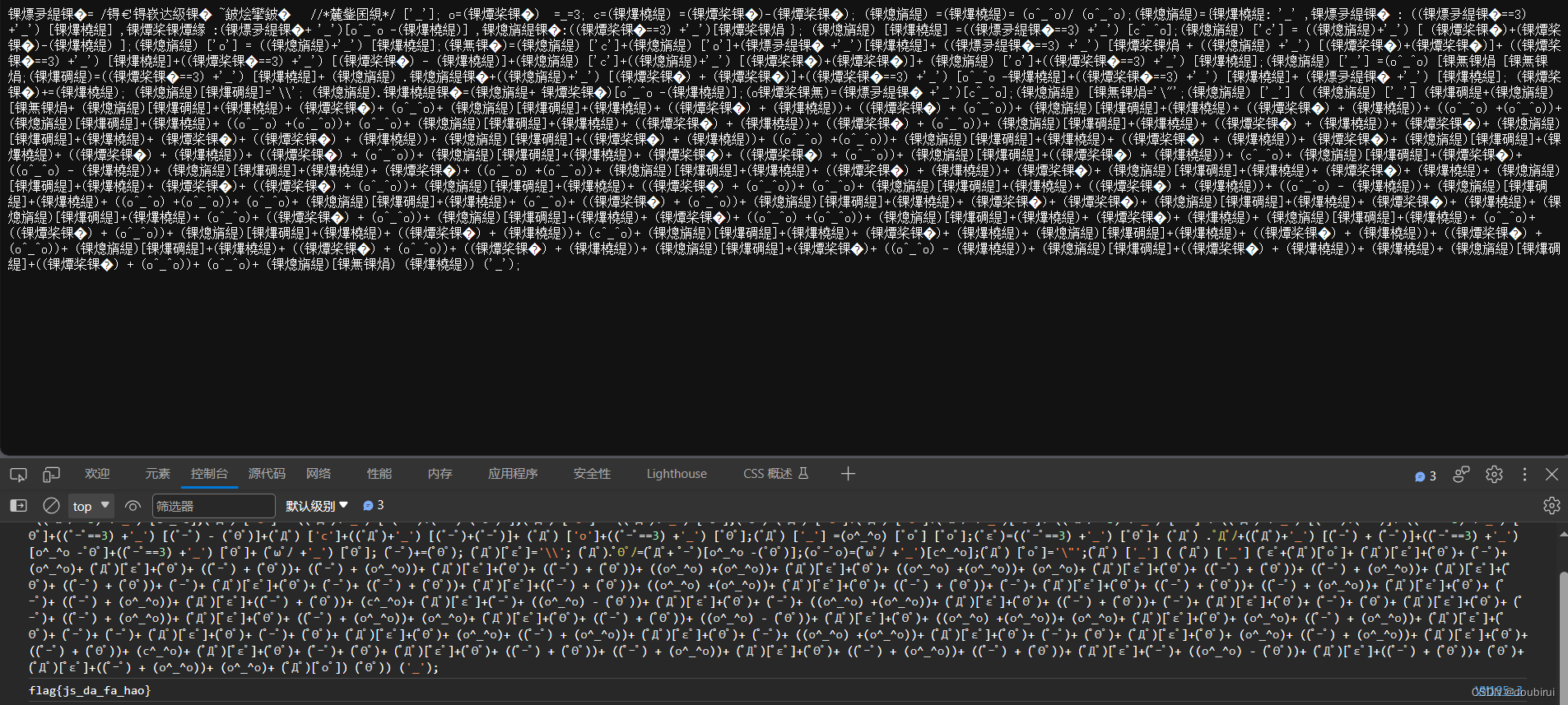
1.观察密码发现密码并不是完全的颜文字，而夹杂着很多的乱码。这时候我们不能直接进行解码，应该先得到正确的颜文字密码之后在进行解码。

2.我们可以将其另存为txt.文件，便可得到正确的颜文字密码。

3.之后可以通过解码工具解码，或者在控制台中复制粘贴回车得到所求flag。

4）crypto4(RAS求私钥：知p q e求d)

公开密钥加密

公开密钥加密，也成为非对称加密，是密码学的一种算法，它需要两个密钥，一个公开密钥，另一个是私有密钥，一个用作加密的时候，另一个则用作解密。

• 明文：需要加密的内容，成为明文。

• 密文：使用密钥把明文加密后的内容。只能用相应的另一个密钥才能解密得到原来的明文。甚至连最初用来加密的密钥也不能用作解密。

对称加密&&非对称加密

对称加密：加密和解密都是用同一个密钥的算法，称作对称加密

（1）甲方选择某一种加密规则，对信息进行加密：

（2）乙方使用同一种规则，对信息进行解密。

非对称加密：加密和解密需要不同的密钥

（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的；

（2）甲方获得乙方的公钥，然后用它对信息进行加密；

（3）乙方得到加密后的信息，用私钥进行解密。

加密过程

在数学上d(c(x))=x,来表示加密解密过程。

这里我们使用典型的爱丽丝与鲍勃假设来解释(来自维基)。

• 1.爱丽丝与鲍勃事先互不认识，也没有可靠安全的沟通渠道，但爱丽丝现在却要通过不安全的互联网向鲍勃发送消息。

• 2.爱丽丝撰写好原文，原文在未加密的状态下称之为明文x。

• 3.鲍勃使用密码学安全伪随机数生成器产生一对密钥，其中一个作为公钥c,另一个作为私钥d.

• 4.鲍勃可以用任何方法发送公钥c给爱丽丝，即使伊夫在中间窃听到c也没关系。

• 5.爱丽丝用公钥c把明文x进行加密，得到密文c(x).

• 6.爱丽丝可以用任何方法传输密文c(x)给鲍勃，即使伊夫在中间窃听到密文c(x)也没问题。

• 7.鲍勃收到密文，用自己的私钥d对密文进行解密d(c(x))，得到爱丽丝撰写的明文x.

• 8.由于伊夫没有得到鲍勃的私钥d,所以无法得知明文x.

• 9.如果爱丽丝丢失了她自己撰写的原文x，在没有得到鲍勃的私钥d的情况下，她的处境将等同伊夫，既无法通过鲍勃的公钥c和密文c(x)重新得到原文x.

什么是RSA

RSA是一种公钥密码算法，它的名字是由它的三位开发者，即Ron Rivest、Adi Shamir 和 Leonard Adleman的姓氏的首字母组成的( Rivest-Shamir-Adleman )。

RSA可被用于公钥密码和数字签名。

RSA加密

在RSA中，明文、密钥和密文都是数字。RSA的加密过程可以用下列公式来表达：

密文=明文E mod N (RSA加密)

RSA的密文是对代表明文的数字的E次方求mod N的结果。换句话说，就是将 明文和自己做E次乘法,然后将其结果除以N求余数，这个余数就是密文。

加密公式中出现的两个数E和 N，到底都是什么数呢? RSA的加密是求明文的 E次方mod N，因此只要知道E和N这两个数，任何人都可以完成加密的运算。所以说，E 和 N是RSA加密的密钥，也就是说，E 和 N的组合就是公钥。

RSA解密

RSA的解密和加密一样简单，可以用下面的公式来表达:

明文=密文 D mod N ( RSA解密)

表示密文的数字的D次方求 mod N就可以得到明文。

这里所使用的数字N和加密时使用的数字N是相同的。数 D 和数 N 组合起来就是RSA的解密密钥，因此D和N的组合就是私钥。

在RSA中，加密和解密的形式是相同的。加密是求“明文的E次方的 mod N”，而解密则是求“密文的D次方的 mod N”。

生成密钥对

在RSA中，加密是求“明文的E次方的mod N”，而解密则是求“密文的D次方的mod N”。

由于E和N是公钥，D和N是私钥，因此求E、D和N这三个数就是生成密钥对。RSA密钥对的生成步骤如下：

1.求N

2.求L（L是仅在生成密钥对的过程中使用的数）

3.求E

4.求D

求N

首先准备两个很大的质数。这两个很大的质数为p和q。p、q太小的话，密码会变得容易破译，但太大的话计算时间又会变得很长。

判断一个数是不是质数并不是看他能不能分解质因数，而是通过数学上的判断方法来完成。

准备好两个很大的质数之后，我们将这两个数相乘，其结果就是N。也就是说，数N可以用下列公式来表达：

N = p x q (p、q为质数)

求L

L这个数在RSA的加密和解密过程中都不出现，它只出现在生成密钥对的过程中。

L是p-1和q-1的最小公倍数。

如果用Icm(X,Y)来表示“X和Y的最小公倍数”，则L可以写成下列形式。

L = Icm(p-1,q-1) (L是p-1和q-1的最小公倍数)

求E

E是一个比1大。比L小的数。此外，E和L的最大公约数必须为1。

如果用gcd(X,Y)来表示X和Y的最大公约数，则E和L之间存在下列关系。

1 < E < L

gcd(E,L) = 1

求D

数D是由数E计算得到的。D、E和L之间必须具备下列关系。

1 < D < L

E x D mod L = 1

解题过程

import gmpy2
p=447685307
q=2037
e=17
phi_n = (p-1)*(q-1)
print("d:",gmpy2.invert(e,phi_n))
# d: 53616899001

5）crypto5(知p q e c求d)

解题过程

import gmpy2 p = 447685307 q = 2037 e = 17 c = 704796792 n = p * q phi_n = (p-1)*(q-1) d = gmpy2.invert(e,phi_n) print("m:",pow(c,d,n))

# m: 904332399012