【数据结构】了解线段树与操作线段树的基本方法

📣 📣 📣 📢📢📢
☀️☀️你好啊！小伙伴，我是小冷。是一个兴趣驱动自学练习两年半的的Java工程师。
📒 一位十分喜欢将知识分享出来的Java博主⭐️⭐️⭐️，擅长使用Java技术开发web项目和工具
📒 文章内容丰富：覆盖大部分java必学技术栈，前端，计算机基础，容器等方面的文章
📒 如果你也对Java感兴趣，关注小冷吧，一起探索Java技术的生态与进步，一起讨论Java技术的使用与学习
✏️高质量技术专栏专栏链接: 微服务，数据结构，netty，单点登录，SSM ，SpringCloudAlibaba等
😝公众号😝 ： 想全栈的小冷，分享一些技术上的文章，以及解决问题的经验
⏩当前专栏：数据结构系列
⏩专栏代码地址: 数据结构代码地址

线段树与操作线段树的基本方法

认识线段树

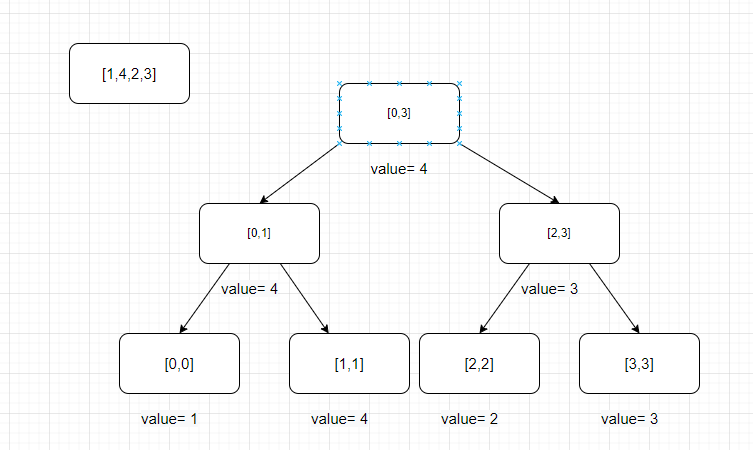
序列 【1,4,2,3】

1. 给序列的第i个数,加上X A[i]=A[I]+X O(1)
2. 取序列的最大的数,遍历最大值 O(N)
3. 遍历的时候 时间复杂度高,怎么处理呢?

线段树Segment Tree

“区间” 线段树是根据区间的性质来构造的

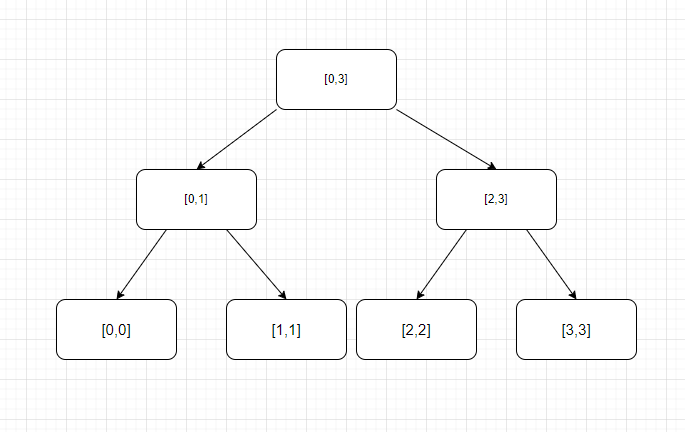
特点:

每次将区间的长度一分为二,区间存储的左右边界 [[start,end]/[left,right]]

如果假设数组的长度 = n 线段树的高度就是 log(n)

将区间中的最大值加入进来,线段树加入值之后就是如下状态

除此之外,可以存储的区间内的最小值,区间求和等等

线段树的节点个数为 n+n/2+n/4… = (1+1/2+1/4…)*n ≈ 2n

构造线段树的时间复杂度和空间复杂度均为 O(n)

线段树创建代码实现

package com.hyc.DataStructure.SegmentTree;

/**
 * @projectName: DataStructure
 * @package: com.hyc.DataStructure.SegmentTree
 * @className: SegmentTree
 * @author: 冷环渊 doomwatcher
 * @description: TODO
 * @date: 2022/2/26 10:15
 * @version: 1.0
 */
public class SegmentTree {
    @Override
    public String toString() {
        return "SegmentTree{" +
                "start=" + start +
                ", end=" + end +
                ", val=" + val +
                ", left=" + left +
                ", right=" + right +
                '}';
    }

    public static void main(String[] args) {
        int[] arr = {1, 4, 2, 3};
        SegmentTree root = SegmentTree.build(arr);
        System.out.println(root);
    }

    //节点区间范围
    public int start, end;
    //    存储节点值
    public int val;
    //    左右子树
    public SegmentTree left;
    public SegmentTree right;

    public SegmentTree(int start, int end, int val) {
        this.start = start;
        this.end = end;
        this.val = val;
    }

    public static SegmentTree build(int[] A) {
        return buildByRecu(0, A.length - 1, A);
    }

    public static SegmentTree buildByRecu(int start, int end, int[] A) {
        if (start > end) {
            return null;
        }
        SegmentTree root = new SegmentTree(start, end, A[start]);
        //    如果是叶子节点 直接返回
        if (start == end) {
            return root;
        }
        //    如果不是那么就以二分的形式来递归创建树
        int mid = (start + end) / 2;
        root.left = buildByRecu(start, mid, A);
        root.right = buildByRecu(mid + 1, end, A);
        //求出区间内最大值为父节点的val
        root.val = Math.max(root.left.val, root.right.val);
        return root;
    }
}

单点更新

    public static void modify(SegmentTree root, int index, int value) {
        //    先找到叶子节点,然后逐渐上层
        if (root.start == root.end && root.start == index) {
            root.val = value;
            return;
        }

        int mid = (root.start + root.end) / 2;
        //    判断index 在左子树的区间,还是 右子树的区间,二分思路
        if (index <= mid) {
            modify(root.left, index, value);
            root.val = Math.max(root.left.val, root.right.val);
            return;
        }
        modify(root.right, index, value);
        root.val = Math.max(root.left.val, root.right.val);
    }

搜索线段树

搜索线段树返回索引值

    public static int searchByIndex(SegmentTree root, int index) {
        //    先找到叶子节点,然后逐渐上层
        if (root.start == root.end && root.start == index) {

            return root.val;
        }

        int mid = (root.start + root.end) / 2;
        //    判断index 在左子树的区间,还是 右子树的区间,二分思路
        if (index <= mid) {
            searchByIndex(root.left, index);

            return root.val;
        }
        searchByIndex(root.right, index);
        return root.val;
    }