大家好啊,我是董董灿。
刚开始做程序开发时,在公司提交代码前,都需要让大佬们 review(评审),大佬们看完,总会在评论区打出一串"LGTM"。
当时作为小白的我,天真地以为大佬觉得我提交的代码还不错,在开玩笑的夸我说"老哥太猛"。
后来才知道,这原来是 review 的一种黑话,Look Good To Me(LGTM) 的意思,也就是说"我觉得没问题"。
后来学算法,看到了 LSTM,心想这又是什么意思呢。
1、 什么是 LSTM
LSTM(Long Short Term Memory),长短时记忆,是一种特殊的循环神经网络。昨天的那篇文章介绍 Seq2Seq 的时候说过, LSTM 实际上就是一种 Seq2Seq 结构。
这个网络主要是用来处理具有时间序列的数据任务,比如文本翻译、文本转语音等等。
网上关于 LSTM 的文章其实有很多,但我当时学习的时候却感觉很难受,因为很多文章基本上来就是公式一扔,三个门一讲就完事儿了。
作为小白看完之后,依然学不到东西,并且很难对这个算法有一个感性的认识。
后来查阅了很多资料,不记得在哪篇文章或者哪个视频里看到了一个关于这个算法的详解,印象很深,今天就和大家来分享一下。
请跟上下面的思路,文章不长,读完后,希望你会对 LSTM 有一个全新的认识。
2、从一个考试的例子出发来理解 LSTM
首先我们假设一个场景,我们是大学生,目前正处于期末考试阶段,并且已经考完了线性代数,接下来还有一门高数要考。
而我们作为学生,很自然的要开始复习(学习)高数的内容了。
在这个场景中,使用 LSTM 来处理这种带有时间序列的任务,即考完了线性代数,接着去学习高数。
我们来看看,LSTM是怎么和人一样,学到了高数的内容的。虽然不打算说太多技术细节,但是 LSTM 里的一些概念还是要结合例子来说。
首先,LSTM的结构大致如下面这样。
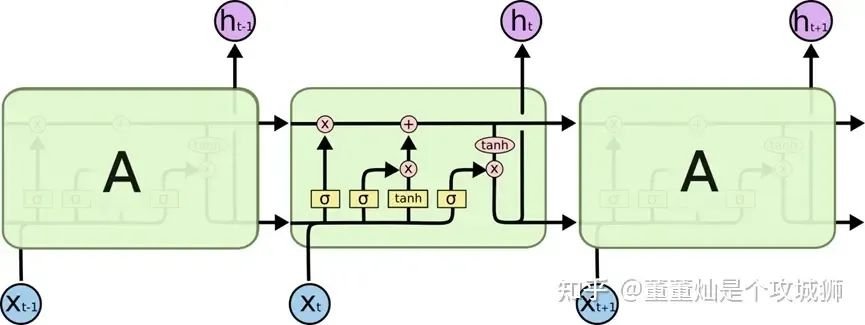
我们只看中间的一个方框,他接受了前面方框的两个输出(一个是上一层真正的输出状态,对应上面的黑色箭头;一个是上一层输出的隐藏状态,对应下面的输出箭头),同时接受了一个新的 Xt 作为输入。
好,那我们就从这里开始。
我们现在要参加高数考试了,在学习高数知识。
我们肯定是希望把所有与高数有关的内容都记住,与高数无关的都忘掉,最好就是在参加高数考试时,大脑里全是高数知识,其他的物理化学知识全部忘掉。
我们从中间大方框的最左边来分析。
首先这个时候,我们接受了上一个单元时刻的输出,上一个时刻我们考线性代数,输出的状态是刚考完线性代数的状态。
那我们这个时候最想做的是什么?当然是把之前学的与本次考高数无关的都忘掉(选择性遗忘)。
为什么说是选择性遗忘呢?
我们上一场考的是线性代数,那本场接着考高数,其实线性代数和高数之间还是有很多知识相关的,所以这个时候我们肯定希望把相关的部分留下来,把不相关的忘掉。
那如果上一场我们考的是英语,那么大概率所有知识都是不相关的,我们几乎都可以忘掉。
说到这,怎么把上一个方框单元的输出状态进行选择性遗忘呢?这里就遇到了 LSTM 结构中的第一个门 —— 遗忘门。
遗忘门
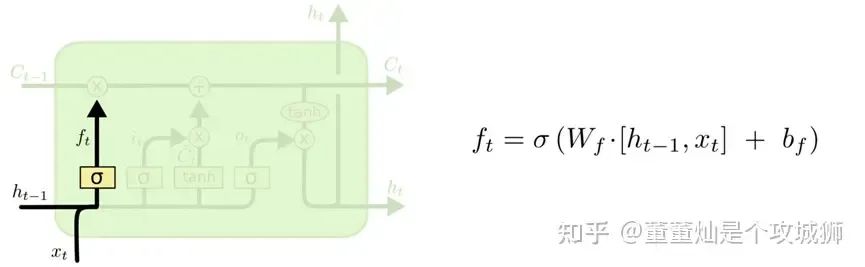
我们可以看到,第一个遗忘门是由一个激活函数和一个乘法来完成的。
它接受了本次状态的信息(xt),也就是我们正在复习的高数的知识,同时接受了上一个方框单元的隐藏状态(ht-1, 上一场考试后我们的大脑状态),然后通过激活函数后与上一个单元的输出(Ct-1)做乘法。
形象的解释一下这个过程:我们学习了高数的内容(xt),大脑中还保留了一部分上一场线性代数的内容,也就是隐藏状态(ht-1),这两个状态经过激活函数激活,选择性的保留,谁的权重大,那么谁最后保留下来的信息就多。
所以,这一步,我们刻苦复习高数和不刻苦复习高数,对应 xt 的权重是不一样的,肯定刻苦复习高数会使得高数的权重更大,那么保留下来的信息就多。
经过激活函数之后,我们认为保留下来的更多的是和高数有关的信息。
那么这个信息去和上一场考试完成时的输出状态相乘(得到的信息就是和高数有关的信息(这个信息会继续往后传),其余的与高数无关的信息由于激活后几乎为零,也就被遗忘了。
到了这,我们把之前该遗忘的都遗忘了,但是要参加高数考试,光遗忘(清空大脑无用信息)是远远不够的,更重要的是要把我们学到的高数知识(xt)给记住。
那我们需要给大脑输入新学到的高数知识,也就是 LSTM 要学习高数知识,接下来就到了第二个门 - 输入门。
输入门
从名字也很好理解,输入本层想学的知识,所以叫做输入门。
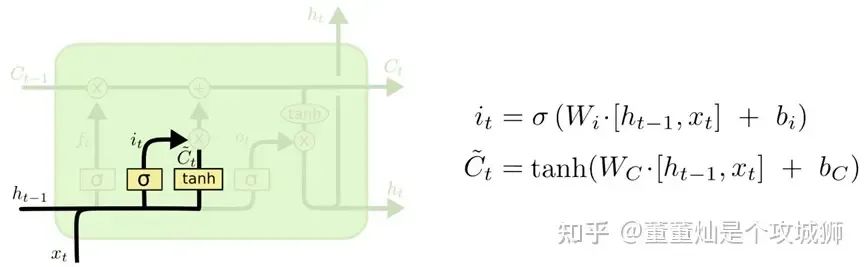
看上图,本次学习的高数知识(xt)和上次隐层的状态结合后,通过一个激活,然后还通过了一个 tanh,然后两者相乘。
本次的激活与遗忘门的激活不同之处在于,遗忘门的激活输出是作用在上一层的输出上,而输入门的激活是作用在 tanh 的输出上。
通俗的理解,这样会选择我们本次学习的高数的内容(因为不是所有的高数内容都会被考到),两者相乘起到一个信息过滤的作用,乘法的输出为提纯后的高数知识(这些高数知识大概率会被考到)。
然后和上面经过遗忘门筛选过的信息相加,就得到了一个新的考高数时的知识库(在这里,有上一层(考完线性代数后)遗留下来的与高数考试相关的知识,比如加减乘除等通用运算知识,也有本次复习高数之后经过提纯的知识,比如微积分,可以说是必考题)。
那到了这一步,基本上我们就可以去参加考试了,下面就是输出门。
输出门
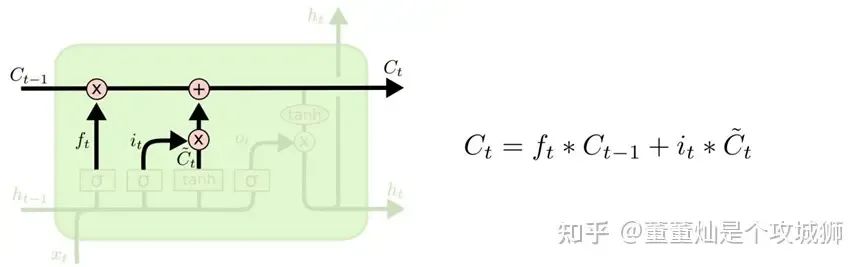
输入门和遗忘门的信息相加之后(Ct),直接输出到下一层。
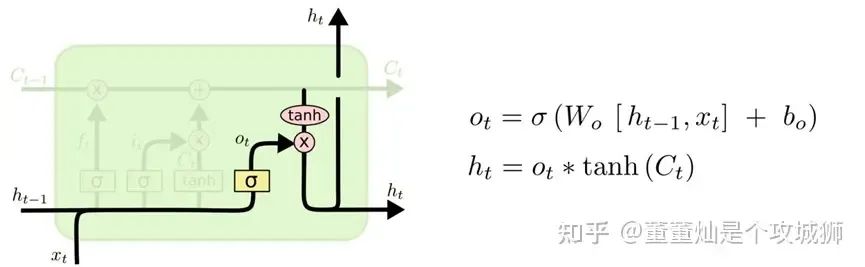
输出门还有个分支,xt 通过激活之后和tanh的输出相乘,然后作为隐藏状态传给下一层。
那这是在干嘛呢?
还记得我们的目的是干什么?考试。
这里就理解为正在考高数好了,带着之前提纯过的知识以及本次学的知识,做了几道高数题,然后考完了高数(又是一次信息过滤,只记住了考完高数后的考的那几道题),作为隐藏状态传给下一层。
有可能下层又要考数理统计了,数理统计可能又要用到本层的高数知识以及前一层的线性代数的知识了,又一个循环,直到所有的考试结束。
这里我们用一个考试的例子,通俗的描述了下遗忘门、输入门和输出门的作用,以及 LSTM 是如何做到选择性遗忘和信息过滤的,希望能帮助到学习 LSTM 的你。
至于为什么在LSTM中,遗忘门可以遗忘掉我们不想要的信息,输入门可以提纯信息,输出门去考试的时候可以发挥最好的状态去做题呢?
可以认为是训练 LSTM 网络的事了。在训练LSTM的时候,最终网络收敛会得到一系列的权值,用于帮助遗忘门更好的遗忘,输入门更好的输入,输出门更好的输出。
最后,一些技术细节比如为什么要选 sigmoid 激活函数,感兴趣的话可以去搜一下,这里不再赘述了。
希望你看完本文后,能对 LSTM 这一算法有个感性的认识。
文中的部分表述来源于之前看过的文章或者视频中的讲解,找不到出处了,如果有同学知道来源,可以在评论区留言,给作者署一下名。





 本文通过大学考试复习的场景,浅显易懂地介绍了LSTM的工作原理,涉及遗忘门、输入门和输出门的选择性遗忘、信息过滤功能。作者强调了LSTM在处理时间序列任务中的应用,并提到了模型训练中的权值调整对于算法表现的重要性。
本文通过大学考试复习的场景,浅显易懂地介绍了LSTM的工作原理,涉及遗忘门、输入门和输出门的选择性遗忘、信息过滤功能。作者强调了LSTM在处理时间序列任务中的应用,并提到了模型训练中的权值调整对于算法表现的重要性。


















 1195
1195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










