Arc of Dream
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)Total Submission(s): 126 Accepted Submission(s): 44
Problem Description
An Arc of Dream is a curve defined by following function:
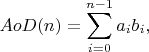
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
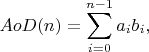
where
a 0 = A0
a i = a i-1*AX+AY
b 0 = B0
b i = b i-1*BX+BY
What is the value of AoD(N) modulo 1,000,000,007?
Input
There are multiple test cases. Process to the End of File.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Each test case contains 7 nonnegative integers as follows:
N
A0 AX AY
B0 BX BY
N is no more than 10 18, and all the other integers are no more than 2×10 9.
Output
For each test case, output AoD(N) modulo 1,000,000,007.
Sample Input
1 1 2 3 4 5 6 2 1 2 3 4 5 6 3 1 2 3 4 5 6
Sample Output
4 134 1902
Author
Zejun Wu (watashi)
Source
Recommend
zhuyuanchen520
题意:略。
思路:公式法。
很笨的方法。
有三种情况
1、 如果Ax 和 Bx 为1时, an, bn都是等差数列。
2、其中一个为1时,就是等差 * 等比.
3、否则是等比 * 等比。
计算得Cn 然后, 算Sn.
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
//
const int V = 100000 + 50;
const int MaxN = 500 + 5;
const int mod = 1000000007;
const int inf = 1987654321;
__int64 n, A0, Ax, Ay, B0, Bx, By;
__int64 Quick_Pow(__int64 a, __int64 b) {
__int64 res = 1;
while(b) {
if(b & 1)
res = (res * a) % mod;
b /= 2;
a = (a * a) % mod;
}
return res % mod;
}
__int64 f() {
__int64 a = ((A0 * (Ax - 1) + mod) % mod + Ay % mod) % mod;
__int64 b = ((B0 * (Bx - 1) + mod) % mod + By % mod) % mod;
__int64 c = Quick_Pow(Ax, n) * Quick_Pow(Bx, n) % mod - 1;
c = (c + mod) % mod;
__int64 d = (Ax * Bx - 1 + mod) % mod * (Ax - 1 + mod) % mod * (Bx - 1 + mod) % mod;
__int64 e = Quick_Pow(d, mod - 2);
return (a * b % mod * c % mod * e % mod);
}
__int64 g() {
__int64 a = ((B0 * (Bx - 1) + mod) % mod + By % mod) % mod;
__int64 b = 1 - Quick_Pow(Bx, n);
b = (b + mod) % mod;
__int64 c = ((Ax - 1) * (Bx - 1) + mod) % mod * ((Bx - 1 + mod) % mod) % mod;
__int64 d = Quick_Pow(c, mod - 2);
return (Ay % mod * a % mod * b % mod * d % mod);
}
__int64 h() {
__int64 a = ((A0 * (Ax - 1) + mod) % mod + Ay % mod) % mod;
__int64 b = 1 - Quick_Pow(Ax, n);
b = (b + mod) % mod;
__int64 c = ((Bx - 1) * (Ax - 1) + mod) % mod * ((Ax - 1 + mod) % mod) % mod;
__int64 d = Quick_Pow(c, mod - 2);
return (By % mod * a % mod * b % mod * d % mod);
}
int main() {
int i, j, k;
while(~scanf("%I64d", &n)) {
scanf("%I64d%I64d%I64d", &A0, &Ax, &Ay);
scanf("%I64d%I64d%I64d", &B0, &Bx, &By);
__int64 a, b, c, d, e;
if(Ax == 1 && Bx == 1) {//等差*等差
a = (n % mod) * A0 % mod * B0 % mod;
b = (n % mod) * ((n - 1) % mod) % mod * Quick_Pow(2, mod - 2) % mod * ((Ay * B0 % mod + A0 * By % mod) % mod) % mod;
c = (n - 1) % mod * (n % mod) % mod * ((2 * n - 1) % mod) % mod * Quick_Pow(6, mod - 2) % mod * Ay % mod * By % mod;
printf("%I64d\n", ((a + b) % mod + c) % mod);
}
else if(Ax == 1 || Bx == 1) {//等比*等差
if(Bx == 1) {
__int64 temp = B0;
B0 = A0;
A0 = temp;
temp = Bx;
Bx = Ax;
Ax = temp;
temp = By;
By = Ay;
Ay = temp;
}
a = ((B0 * (Bx - 1) + mod) % mod + By % mod) % mod * A0 % mod * Quick_Pow(((Bx - 1) * (Bx - 1) + mod) % mod, mod - 2) % mod;
b = ((B0 * (Bx - 1) + mod) % mod + By % mod) % mod * Ay % mod * Bx % mod * ((Quick_Pow(Bx, n - 1) - 1 + mod) % mod) % mod;
c = ((Bx - 1) * (Bx - 1) + mod) % mod * ((Bx - 1 + mod) % mod) % mod;
b = b * Quick_Pow(c, mod - 2) % mod;
d = (A0 % mod + (n - 1 + mod) % mod * Ay % mod) % mod * (((B0 * (Bx - 1) + mod) % mod + By % mod) % mod) % mod * Quick_Pow(Bx, n) % mod;
c = ((Bx - 1) * (Bx - 1) + mod) % mod;
d = d * Quick_Pow(c, mod - 2) % mod;
e = (n % mod * A0 % mod + n % mod * ((n - 1 + mod) % mod) % mod * Ay % mod * Quick_Pow(2, mod - 2) % mod) % mod * By % mod * Quick_Pow((Bx - 1 + mod) % mod, mod - 2) % mod;
// printf("%I64d %I64d %I64d %I64d\n", a, b, d, e);
printf("%I64d\n", (((d - a + mod) % mod - b + mod) % mod - e + mod) % mod);
}
else {//等比*等比
a = f();
b = g();
c = h();
d = (Ay * By % mod) * (n % mod) % mod * Quick_Pow(((Ax - 1) * (Bx - 1) + mod) % mod, mod - 2) % mod;
printf("%I64d\n", ((((a + b) % mod + c) % mod) + d) % mod);
}
}
}矩阵快速幂
ai = ai-1 * Ax + Ay;
bi = bi-1 * Bx + By;
ai * bi = ai-1 * bi-1 * (Ax * Bx) + ai-1 * (Ax * By) + bi-1 * (Bx * Ay) + AyBy;
Si = Si - 1 + ai * bi = Si - 1 + ai-1 * bi-1 * (Ax * Bx) + ai-1 * (Ax * By) + bi-1 * (Bx * Ay) + AyBy;
根据SI , 一定需要 Si - 1, ai - 1, bi - 1, ai - 1 * bi - 1, 常数。
矩阵大小为5,
构造 初始矩阵A 为 记 S0
[1, A0, B0, A0 * B0, A0 * B0] 即 [1, a0, b0, a0 * b0, S0]
[0 …… 0]
转换矩阵 B. 使得 A * B = S1 = [1, a1, b1, a1 * b1 , S1]
根据上面4个公式得。
第一列为 1, 0, 0, 0, 0;
第二列为 Ay, Ax, 0, 0, 0;
第三列为 By, 0, Bx, 0, 0;
第四列为 AyBy, Ax * By, Bx * Ay, Ax * Bx, 0;
第五列为 AyBy, Ax * By, Bx * Ay, Ax * Bx, 1;
即


N次递推得

现在要求 Sn - 1 , 所以 init * Pow ^ n - 1. 然后取第一行, 第5个元素。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int V = 100000 + 50;
const int mod = 1000000000 + 7;
const int MaxN = 5;
struct Matrix{
__int64 mat[MaxN][MaxN];
};
Matrix init, Pow;
__int64 n, A0, Ax, Ay, B0, Bx, By;
Matrix multi(Matrix a, Matrix b) {
Matrix ans;
for(int i = 0; i < MaxN; ++i)
for(int j = 0; j < MaxN; ++j) {
__int64 sum = 0;
for(int k = 0; k < MaxN; ++k)
sum = (sum + a.mat[i][k] * b.mat[k][j] % mod) % mod;
ans.mat[i][j] = sum;
}
return ans;
}
Matrix MatrixQuickPow(Matrix a, __int64 b) {
Matrix ans = init;
while(b) {
if(b & 1)
ans = multi(ans, a);
b /= 2;
a = multi(a, a);
}
return ans;
}
int main() {
while(~scanf("%I64d", &n)) {
scanf("%I64d%I64d%I64d%I64d%I64d%I64d", &A0, &Ax, &Ay, &B0, &Bx, &By);
if(!n) {
printf("0\n");
continue;
}
init.mat[0][0] = 1;
init.mat[0][1] = A0;
init.mat[0][2] = B0;
init.mat[0][3] = init.mat[0][4] = A0 * B0 % mod;
Pow.mat[0][0] = Pow.mat[4][4] = 1;
Pow.mat[0][1] = Ay;
Pow.mat[0][2] = By;
Pow.mat[0][3] = Pow.mat[0][4] = Ay * By % mod;
Pow.mat[1][1] = Ax;
Pow.mat[2][2] = Bx;
Pow.mat[1][3] = Pow.mat[1][4] = Ax * By % mod;
Pow.mat[2][3] = Pow.mat[2][4] = Ay * Bx % mod;
Pow.mat[3][3] = Pow.mat[3][4] = Ax * Bx % mod;
/*
for(int i = 0; i < MaxN; ++i) {
for(int j = 0; j < MaxN; ++j)
printf("%I64d ", Pow.mat[i][j]);
printf("\n");
}*/
Matrix ans = MatrixQuickPow(Pow, n - 1);
printf("%I64d\n", ans.mat[0][4]);
}
}























 660
660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








