本文详细介绍了《深入理解计算机系统》（CSAPP）实验DataLab的函数实现过程，包括bitXor、tmin、isTmax等13个函数。每个函数的实现思路和代码细节均进行了阐述，旨在通过位级运算实现特定功能。实验在Linux环境下进行，适合熟悉C语言和位操作的读者。
目录
前言
该实验为《深入了解计算机系统》即CSAPP的第一个实验：DataLab，旨在通过位级运算实现一些功能。本文介绍开始实验前需要进行的准备工作以及每个函数具体的实现方式。
一、前期准备
1.需要在linux系统上运行，因此无论是在电脑上装一个linux系统或是使用虚拟机，设法取得一个linux系统，推荐使用虚拟机。
2.推荐使用Vscode编辑器，功能强大。
3.实验内容下载地址： http://csapp.cs.cmu.edu/3e/labs.html
注意下载其中的handout即可。
二、函数实现
1.bitXor
bitXor - x^y using only ~ and &
* Example: bitXor(4, 5) = 1
* Legal ops: ~ &
* Max ops: 14
* Rating: 1
用 ~ 和 & 实现异或运算。
思路
先将x为0且y为1的位找出：(~x) & y；
再将x为1且y为0的位找出：x & (~y)；
最后用或运算 | 相连，但限制使用 | ，因此用~( ~() & ~() )代替。
函数实现
int bitXor(int x, int y) {
return ~(~((~x) & y) & ~(x & (~y)));
//等价于 (~x) & y | x & (~y) |的前者将x为0y为1的位找出，后者将x为1y为0的位找出
}2.tmin
tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
返回int类型能表示的最小值，即Tmin。
思路
根据补码规则，int的最小值为0x80000000，因此将1左移31位即可。
函数实现
int tmin(void) {
return 1 << 31; //int类型有32位，将1左移31位得到最小值负2的32次方
}3.isTmax
isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
如果x为最大值（Tmax）则返回1，否则返回0 。
思路
不难(doge)发现，x为最大值0x7FFFFFFF时，+1后（0x80000000）再取反（0x7FFFFFFF）得到了它本身，而除此（Tmax）之外这个性质仅对于x=-1（0xFFFFFFFF）成立。因此我们想到，先验证x加1取反后与x异或，x为最大值时返回0x00000000=0，取非得到返回值1。同时验证x不等于-1（0xFFFFFFFF），即验证x+1不等于0：x+1与0异或，x=-1时得到0，取非两次得到0.将两种情况进行与运算即可排除x=-1的情况。
函数实现
int isTmax(int x) {
return !((~(x+1))^x) & (!!((x+1)^0));
}4.allOddBits
allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
如果奇数位全为1（0xAAAAAAAA）则返回1，否则返回0 。
思路
先得到奇数位全为1的数(0xAAAAAAAA)，再将x与其比较。
若x满足，x与其与运算后仍为本身，与其异或后为0，取反后为1，返回1；
若x不满足，与运算后存在奇数位为0的位置，异或后这些奇数位为1，取反后为0，返回0.
函数实现
int allOddBits(int x) {
int a_8=0xAA;
int a_16=a_8 | (a_8<<8);
int a_32=a_16 | (a_16<<16); // 获得一个三十二位的奇数位全为1的数
return !((x & a_32)^ a_32);
}5.negate
negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
输出相反数 -x 。
思路
取反再加1即可。
函数实现
int negate(int x) {
return (~x)+1; // 取反+1得到相反数
}6.isAsciiDigit
isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
如果x 在范围之内，返回1，否则返回0.
思路
先通过比较大小判断x是否在范围之内。由于不能使用减法，使用取反加1当作减法。
在判断两个差的符号位，若全为0，则两者都大于等于0，即上面俩式子大于等于0，说明x在此之间。
差为非负符号位为0，判断时取非；同时满足用&连接。
函数实现
int isAsciiDigit(int x) {
int a = x + ((~0x30) + 1); //x-0x30
int b = 0x39 + ((~x) + 1); //0x39-x
a = a >> 31;//得到a和b的符号位，若全为0，则两者都大于等于0，即上面俩式子大于等于0，说明x在此之间
b = b >> 31;
return (!a & !b);
}7.conditional
conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
用位级运算表示三目运算符x ? y : z .
思路
先判断x是否为0.
用0xFFFFFFFF保存y或者z的值，用0x00000000删除y或者z的值。
通过x是否为0构造出上面提到的全0或全1的数其中之一。
x为非0时对应保存y的值删除z的值，x为0时对应保存z的值删除y的值。
有选择时使用 | 连接。
函数实现
int conditional(int x, int y, int z) {
int a = !!x;//判断x是否为0
a = ~a + 1;//x为非0时，a赋值为11111111；x为0时，a赋值为00000000
return (a&y)|((~a)&z); //用11111111&y(z)得到y(z)，用00000000&y(z)得到0，运算后两边有一边为结果，另一边为0，二者|连接得到结果
}8.isLessOrEqual
isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
比较两数大小，小于等于返回1，否则返回0.
思路
需要考虑到溢出的情况：x y同号不溢出，x 有异号会溢出。
不溢出时，正常考虑y-x的符号。
溢出时我们发现：
当y<0 x>0时溢出，y-x的符号yxSign>0;
当y>0 x<0时溢出，yxSign<0。
因此输出结果与xSign相同。
注意到代码中用&1格式化，具体原因见注释部分。
函数实现
int isLessOrEqual(int x, int y) {
int x_negate = (~x)+1; // -x
int add = x_negate + y; // y-x
int yxSign = add>>31 & 1; // y-x的符号
int xSign = x>>31 &1; // x的符号
int ySign = y>>31 &1; // y的符号
int checkSign = xSign^ySign; //判断x y的符号是否相同
/*
x y符号相同时checkSign为0，此时不会溢出，x<=y时yxSign为0，输出!yxSign即可；
x y符号不同时checkSign为1，当y<0 x>0时溢出，yxSign>0;当y>0 x<0时溢出，yxSign<0，因此输出结果与xSign相同；
中间需要&1格式化，否则checkSign=11111111(x y符号不同)且xSign=11111111(x符号为负)时，不格式化会输出11111111 (-1),格式化后为00000001，输出为1；
*/
return (!checkSign & !yxSign) | (checkSign & xSign);
}9.logicalNeg
logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
用其他运算符实现逻辑非 ！ 。
思路
！运算符将0与非零数区分开来。
我们注意到，0的相反数还是0，而其他数和其相反数其中之一为负。这时我们就可以在符号位上做文章。
具体步骤的解释见注释部分。
函数实现
int logicalNeg(int x) {
int neg = x | ((~x)+1);// 0的相反数还是0，除了0之外其他数和其相反数中有一个负数，因此符号位为1
neg = neg >> 31;//其他数得到11111111 = -1；0经过操作后得到00000000 = 0；
return neg+1;//对于其他数返回-1+1=0，对于0，返回0+1=1
}10.howManyBits
howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
计算最少需要几位能用补码表示出x。
思路
运用二分法的思想，减少判断次数。
对于正数，找出其第一个1所在的位置加上符号位即可；对于负数，由于高位全是0，因此找出第一个0所在的位置再加上符号位即可。为了方便，将负数取反按正数的方法做，反正符号位单独算，因此这个操作不影响最终结果。
具体步骤的解释在注释中给出。
函数实现
int howManyBits(int x) {
int sign = x >> 31;//x的符号
x= (sign & (~x)) | ((~sign) & x);//x为正，不变，找出第一个1所在的位置再加上符号位即为所需要的位数
//x为负，取反；因为负数前的许多1与仅有一个1等效，因此负数可认为找第一个0的位置再加上符号位1位得到需要的位数
int b16 = !!(x>>16)<<4;//先看前16位有没有1，若有，给b16赋值16（1<<4）；若没有，赋值的操作为（0<<4）因此不变。
x = x>>b16;//上述情况，若有，x右移16位，接下来比较高位16位中的前八位；若无，此操作下x不变，接下来比较x的前24（8+16）位
int b8 = !!(x>>8)<<3;
x = x>>b8;
int b4 = !!(x>>4)<<2;
x = x>>b4;
int b2 = !!(x>>2)<<1;
x = x>>b2;
int b1 = !!(x>>1);// <<0略去
x = x>>b1;
int b0 = x;//要么x前31位都是0，此时x为0x0或者0x1，x本身的值就是需要的位数；
//要么x=0x80000000，为Tmin，取反后是Tmax，或者本身就是Tmax，前面已经攒了31位，到这b0必然是0，但后面会加上符号位1位
return b16+b8+b4+b2+b1+b0+1;
}11.floatScale2
从这道题开始进入小数部分，首先要了解IEEE浮点表示规则，知道小数是如何用unsigned表示的才能看懂这部分。
floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
计算2 * f 的值。
思路
分为三种情况：
1.指数位==0xFF，特殊值，按要求返回即可
2.指数位==0，非规格化数。
(1) 小数位==0，0*2=0，返回0.
(2)小数位不是0，是一个接近0的很小的数，小数位左移1位即可。
3.指数位为其他情况，*2即指数位左移1位。但是要考虑左移后打到0xFF的情况，这时表示*2后数字非常大，返回无穷，具体返回正无穷还是负无穷还要通过符号位判断。其他正常情况就正常返回。
函数实现
unsigned floatScale2(unsigned uf) {
unsigned s = uf & 0x80000000;//符号位
unsigned exp = (uf & 0x7F800000)>>23;//指数位
unsigned frac = uf & 0x7FFFFF;//小数位
unsigned inf = s | (0xFF << 23);//表示无穷大，由符号位决定是正无穷还是负无穷
if(exp == 0xFF) return uf;//特殊值，frac=0为无穷，frac!=0为NaN，均按要求返回自身
if(exp == 0)//非规格化数
{
if(frac == 0) return uf;//uf就是0，*2还是0
frac = frac << 1;//不然为一个接近0的数，*2直接小数部分*2就是左移一位
return s | (exp<<23) | frac ;
}
exp++;//正常*2即指数位+1（详见浮点数表示的公式即IEEE浮点规则）
if(exp == 0xFF) return inf;//*2后无法被规格化数表示，成为特殊值，返回无穷
return (s | (exp<<23) | frac);//正常返回
}12.floatFloat2Int
floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
将单精度浮点数强制转化为整数。
思路
1.E<0时，表示不是一个整数，小于1，因此返回0即可.
2.E>31时，超过了int的范围，按要求返回0x80000000u.
3.24<=E<=31时，在23位小数均左移的情况下继续左移(E-23)位.
4.0<=E<24时，舍弃小数位不够的（23-E）位，用右移小数位实现此操作。
函数实现
int floatFloat2Int(unsigned uf) {
unsigned s = uf >> 31;//符号位
unsigned exp = (uf & 0x7F800000)>>23;//指数位
unsigned frac = uf & 0x7FFFFF;//小数位
int E = exp - 127;//按照IEEE规则算出的指数
int result =0;
frac = frac | 0x00800000;//M = 1 + frac，得到有效数字
if(E < 0) return 0;//小于1的数，返回0即可
if(E > 31) return 0x80000000u;//2^31以上或一下的数超过int范围，按要求返回0x80000000u
if(E > 23) result = (frac << (E-23));//小数位只有23位，指数大于23相当于把小数位小数点抹掉（左移23位）后继续左移（E-23）位
else result = (frac >> (23-E));//指数不够23，小数位不能完全成为整数位，舍弃不够的（23-E）位
if(s == 1)
return ((~result)+1);//符号为负，返回结果的相反数
else
return result;//正常返回
}13.floatPower2
floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
用单精度浮点数表示2的x次方。
思路
1.x<=-127，数字太小返回0.
2.x>=128，返回阶码最大值.
3.其余情况先考虑阶码的偏移量，此时这个数表示2的次方，再左移回去。
函数实现
unsigned floatPower2(int x) {
if(x<=-127) return 0;
if(x>=128) return 0x7f800000;
return (127+x)<<23;
}三、小结
测试成绩
在终端中打开datalab-handout所在文件夹，依次执行以下命令：
./dlc bits.c
make clean
make btest
./btest
下图是在我的电脑上进行测试的结果：
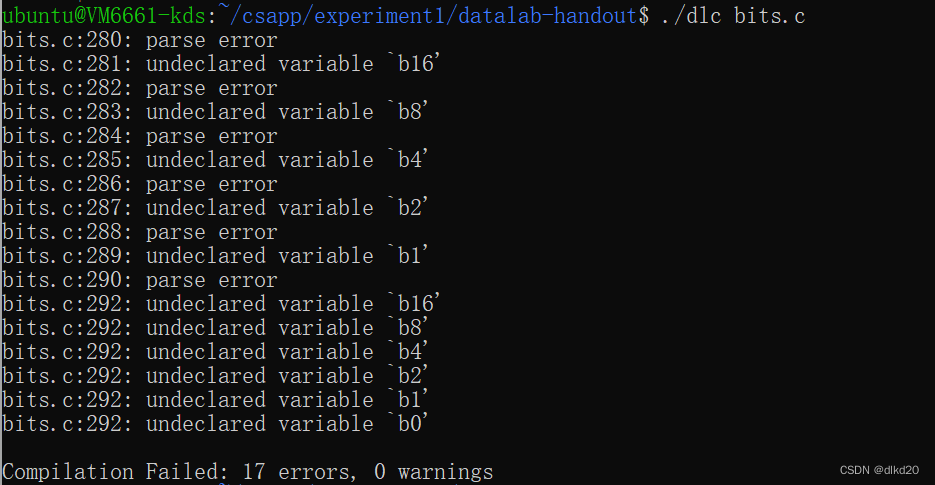
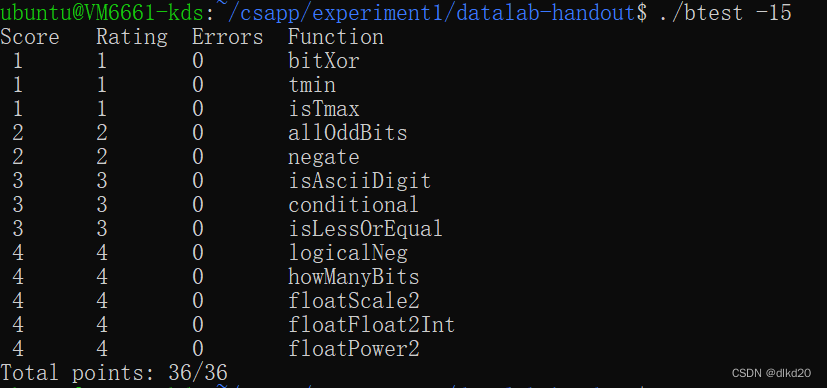
最后一题在默认的10秒检测中超时，因此我改成了15秒（如图）。
最终结果满分咯！
心得体会
datalab是csapp的第一个实验，主要让我们深入了解计算机系统中二进制的使用规则，这其中分为整型和浮点型。由于浮点型有一套人为制定的编码规则，因此理解起来有些难度。这小小的13个实验却几乎涵盖了所有二进制的知识，身为大一新生的我做起来颇具挑战。我在阅读csapp书籍时，二十页就要花费我至少一个半小时的时间细读才能读懂，可见其知识深度。这13个实验对我来说最难的莫过于后三个关于浮点型的实验。如果不事先充分了解其编码规则，做起来十分的困难。不过当看到测试结果一点点由0分变为36分满分时，心情是无比激动的。期待后面的实验！
扫一扫
741
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
