取模与取余

一、定义

对于整型数a，b来说，取模运算或者求余运算的方法都是：
1.求整数商： c = a/b;
2.计算模或者余数： r = a - c*b.
求模运算和求余运算在第一步求整数商时不同：
取余运算在计算c的值时，向0方向舍入(fix()函数)；
取模运算在计算c的值时，向无穷小方向舍入(floor()函数)。

例如：计算-7 Mod 4
那么：a = -7；b = 4；
第一步：求整数商c，如进行求模运算c = -2（向无穷小方向舍入），求余c = -1（向0方向舍入）；
第二部：计算模和余数的公式相同，但因c的值不同，求模时r = 1，求余时r = -3。

二、归纳

1. 当a和b符号一致时，求模运算和求余运算所得的c的值一致，因此结果一致。
2. 当a和b符号不一致时，结果不一样。
   求模运算结果的符号和b（除数）一致，
   求余运算结果的符号和a（被除数）一致。
3. 各个环境下%运算符的含义不同，比如c/c++为取余，而java，python则为取模。

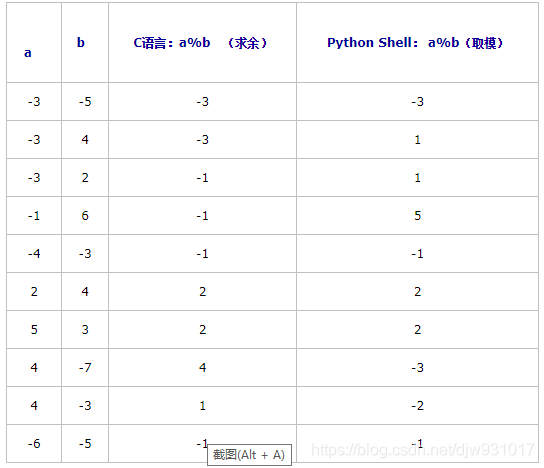
三、实例

下面表格是一些典型的取模或者求余的值。

以上转载：https://www.cnblogs.com/xsfx/p/7122575.html

在实际的编程运用中，取余或取模往往用于循环队列或一些循环列表中。这种情况下，往往需要队尾减去队首，从而产生负数。因为不同语言对%的含义不同，所以要尽量避免出现负数的情况。一般还要加上循环的长度。参考公式为（rear-front+len)%len。