本文详细解析了快速排序（Quicksort）的伪码、真实代码实现及时间复杂度分析，包括其O(nlogn)和最坏情况下的O(n^2)。同时介绍了插入排序算法的过程和代码，并对比了两种排序算法。讨论了二分归并排序的MergeSort和Merge操作，提供了完整的代码实现。
典型实例--快速排序，插入排序
快速排序算法
设被排序的数组是A，快速排序算法的基本思想是用数组的首元素作为标准将A划分成前，后两部分，比首元素小的元素构成数组前部分，比首元素大的元素构成数组的后部分，两个部分构成两个新的子问题，算法接着对这两部分递归地进行排序。
算法的关键在于怎样划分数组A二将其归约成两个子问题。主程序直接调用Quicksort(A,1,n)即可。
伪码描述
Quicksort()排序
void Quicksort(A,p,r)
//输入:数组A[p..r],1<=p<=r<=n
//输出:从A[p]到A[r]按照递增顺序排好的数组A
{
if(p<r)
{
q=Partition(A,p,r);//划分数组，找到首元素A[p]在排好序后的位置q
A[p]<->A[q];
Quicksort(A, p, q - 1);
Quicksort(A, q + 1, r);
}
}
查找首元素的位置Partition()
Partition()的作用是，将首元素(相当于一个哨兵)放置到一个合适的位置，这个位置之前的元素都比首元素小，这个元素之后的位置都比首元素大。
int Partition(A,p,r)
//输入:数组A[p..r]
//输出:j,A的首元素在排好序的数组中的位置
{
x=A[p];
i = p;//首位置
j = r+1;//末位置，注意因为伪码是先j=j-1，而真实实现先比较，所以j=r
while(true)
{
repeat j = j - 1;//
until A[j] <= x;
repeat i = i + 1;
until A[i] > x;
if (i<j)
A[i]<->A[j];
else return j;
}
}
真实代码实现
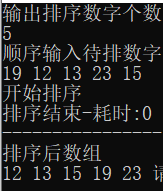
输入数字个数
5
输入待排数组
19 12 13 23 15
/*
* @Description:
* @Author: dive668
* @Date: 2021-05-14 19:50:18
* @LastEditTime: 2021-05-14 20:28:33
*/
#include <iostream>
#include <ctime>
using namespace std;
void exchange(int& a,int &b)
{
int temp;
temp = a;
a = b;
b = temp;
}
int Partition(int A[],int p,int r)
{
//输入:数组A[p..r]
//输出:j,A的首元素在排好序的数组中的位置
int i, j;
int x=A[p];//哨兵
i = p;
j = r;
while(true)
{
while(A[j]>x)
j = j - 1;
while(A[i]<=x)
i = i + 1;
if (i<j)
exchange(A[i],A[j]);
else return j;//while循环出口
}
}
void Quicksort(int A[],int p,int r)
//输入:数组A[p..r],1<=p<=r<=n
//输出:从A[p]到A[r]按照递增顺序排好的数组A
{
int q;
if(p<r)
{
q=Partition(A,p,r);//划分数组，找到首元素A[p]在排好序后的位置q
exchange(A[p], A[q]);
Quicksort(A, p, q - 1);
Quicksort(A, q + 1, r);
}
}
int main()
{
int n;
clock_t t;
cout << "输出排序数字个数" << endl;
cin >> n;
int *a = new int[n + 1];
a[0] = 0;
cout << "顺序输入待排数字"<<endl;
for (int i=1; i <= n;++i)
{
cin >> a[i];
}
cout<<"开始排序"<<endl;
t = clock();
Quicksort(a, 1, n);
cout<<"排序结束"<<"-"<<"耗时:"<<clock()-t<<endl;
cout << "----------------" << endl;
cout << "排序后数组" << endl;
for (int i=1; i <= n;++i)
{
cout << a[i]<<" ";
}
system("pause");
return 0;
}
时间复杂度分析 O ( n l o g n ) O(nlogn) O(nlogn)和 O ( n 2 ) O(n^2) O(n2)
划分工作量是
O
(
n
)
O(n)
O(n)，一位内每个元素都需要和首元素进行1次比较。
除了这个工作量外，就是两个子问题递归调用的工作量。
T
(
n
)
=
2
T
(
n
/
2
)
+
O
(
n
)
T(n)=2T(n/2)+O(n)
T(n)=2T(n/2)+O(n)
T
(
1
)
=
0
T(1)=0
T(1)=0
得到时间复杂度为
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
考虑极端不平衡的情况，即划分后的子问题的规模一个是0，另一个是n-1的情况。当输入是从小到大的序列或者是从大到小的逆序列时就会呈现这种划分。
这时的时间复杂度为
T
(
n
)
=
T
(
n
−
1
)
+
O
(
n
)
T(n)=T(n-1)+O(n)
T(n)=T(n−1)+O(n)
T
(
1
)
=
0
T(1)=0
T(1)=0
得到最坏情况下的复杂度为
O
(
n
2
)
O(n^2)
O(n2)
插入排序算法
插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
算法描述
一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：
1.从第一个元素开始，该元素可以认为已经被排序；
2.取出下一个元素，在已经排序的元素序列中从后向前扫描；
3.如果该元素（已排序）大于新元素，将该元素移到下一位置；
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5.将新元素插入到该位置后；
6.重复步骤2~5
动画演示
设输入是n个数组A[1…n]
真实代码实现
void insertSort(int A[],int n)//传入数组和最大下标
{
int x,i,j;
for (i = 2; i <= n;++i)//默认第一个元素已经是有序的，所以从第二个元素开始
{
x = A[i];
j = i - 1;//取出下一个元素,在已经排序的元素序列中从后向前扫描
while(j>0&&A[j]>x)//在已经排序的元素序列中从后向前扫描
{//如果该元素（已排序）大于新元素，将该元素移到下一位置
A[j + 1] = A[j];
j = j - 1;
}
A[j + 1] = x;//直到找到已排序的元素小于或者等于新元素的位置
}
}
二分归并排序算法
将被排序的数组分成相等两个数组，然后使用相同的算法对两个子数组分别排序，最后将两个排好序的数组归并成一个数组。
例如对8个数的数组L进行排序，先将L划分成L[1…4]和L[5…8]两个子数组，然后分别对这两个子数组进行排序。子数组的排序方法与原来数组的方法一样，以L[1…4]的排序为例，先将L[1…4]划分成L[1…2]和L[3…4]两个更小的子数组，分别对他们排序，然后进行归并。当对更小的数组L[1…2]进行排序时，按照算法需要进一步划分。划分结果是L[1]和L[2]，各含有1个元素，不再需要排序。这时算法将停止递归调用并开始归并。对于其他子问题，算法也同样处理。
伪码描述MergeSort()
MergeSort(A,p,q)
void MergeSort(int A[],int p,int r)
//输入：数组A[p..r],1<=p<=r<=n
//输出：从A[p]到A[r]按照递增顺序排好序的数组A
{
int q;
if(p<r)
{
q = (p + r) / 2;
MergeSort(A, p, q);
MergeSort(A, q + 1, r);
Merge(A, p, q, r);
}
}
伪码描述Merge()
Merge()函数是将两个排好序的小数组A[p…q]与A[q+1…r]合并成一个排好序的大数组。归并的基本思想是：将这两个小数组分别复制到B与C中，A变成空数组，用来存放排好序的大数组。接着，算法比较B与C的首元素，如果哪个首元素比较小，就把它移到A中，比较1次，移走一个元素。如果其中一个变成空数组，那么就把剩下那个的所有元素顺序复制到A中，用伪码描述，过程如下：
//输入：按照递增顺序排好序的数组 A [ p . . q ] A[p..q] A[p..q]与 A [ q + 1.. r ] A[q+1..r] A[q+1..r]
//输出：按照递增顺序排好序的数组 A [ p . . r ] A[p..r] A[p..r]
void Merge(A,p,q,r)
{
int i,j,k;
int x=q-p+1;int y=r-q;
//将A[p..q]复制到B[1..x]，将A[q+1..r]复制到C[1..y]
int *B = new int[x + 1];
int *C = new int[y + 1];
for(i=p;i<=q;++i)
{
B[i-p+1]=A[i];
}
for(i=q+1;i<=r;++i)
{
C[i-q]=A[i];
}
i=1,j=1,k=p;
while(i<=x&&j<=y)
{
if(B[i]<=C[j])
{
A[k]=B[i];
++i;
}
else
{
A[k]=C[j];
++j;
}
++k;
}
//if(i>x) then 将C[j..y]复制到A[k..r]//i所在数组复制完而越界
if(i>x)
{
for(i=j;i<=y;++i)//i已经失去作用，拿来做变量
{A[k]=C[i];++k;}
}
//else 将B[i..x]复制到A[k..r]//j所在数组复制完而越界
else
{
for(j=i;j=<x;++j)
{A[k]=B[j];++k;}
}
}
二分归并完整代码实现
#include <iostream>
using namespace std;
void Merge(int A[],int p,int q,int r)
{
int i,j,k;
int x=q-p+1;int y=r-q;
int *B = new int[x + 1];
int *C = new int[y + 1];
B[0] = C[0] = 0;
//将A[p..q]复制到B[1..x]，将A[q+1..r]复制到C[1..y]
for(i=p;i<=q;++i)
{
B[i-p+1]=A[i];
}
for(i=q+1;i<=r;++i)
{
C[i-q]=A[i];
}
i=1,j=1,k=p;
while(i<=x&&j<=y)
{
if(B[i]<=C[j])
{
A[k]=B[i];
++i;
}
else
{
A[k]=C[j];
++j;
}
++k;
}
//if(i>x) then 将C[j..y]复制到A[k..r]//i所在数组复制完而越界
if(i>x)
{
for(i=j;i<=y;++i)//i已经失去作用，拿来做变量
{
A[k]=C[i];
++k;
}
}
//else 将B[i..x]复制到A[k..r]//j所在数组复制完而越界
else
{
for(j=i;j<=x;++j)
{
A[k]=B[j];
++k;
}
}
}
void MergeSort(int A[],int p,int r)
//输入：数组A[p..r],1<=p<=r<=n
//输出：从A[p]到A[r]按照递增顺序排好序的数组A
{
int q;
if(p<r)
{
q = (p + r) / 2;
MergeSort(A, p, q);
MergeSort(A, q + 1, r);
Merge(A, p, q, r);
}
}
int main()
{
int n;
clock_t t;
cout << "输出排序数字个数" << endl;
cin >> n;
int *a = new int[n + 1];
a[0] = 0;
cout << "顺序输入待排数字"<<endl;
for (int i=1; i <= n;++i)
{
cin >> a[i];
}
cout<<"开始排序"<<endl;
t = clock();
MergeSort(a,1, n);
cout<<"排序结束"<<"-"<<"耗时:"<<clock()-t<<endl;
cout << "----------------" << endl;
cout << "排序后数组" << endl;
for (int i=1; i <= n;++i)
{
cout << a[i]<<" ";
}
system("pause");
return 0;
}
选择问题
选择问题通常出现在实际应用中，最常见的是选最大，选最小，选中位数，选第二大等，这些问题可以给出统一的描述。
设L是n个元素的集合，从L中选出第k小的元素，其中1<=k<=n。这里的第k小的元素是指：当L中元素按照从小到大排好序之后，排在第k个位置的元素。当k=1时，选出的就是最小的元素，当k=n时，选出的就是最大元素。当k=n-1时，选出的计时第二大元素，当k=[n/2]就是中位数。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
