【PTA-python】第4章-4 验证“哥德巴赫猜想” (20 分)--拆解素数

最新推荐文章于 2023-11-07 22:03:39 发布

原创最新推荐文章于 2023-11-07 22:03:39 发布 · 1.7k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#python

PTA-python 专栏收录该内容

51 篇文章

订阅专栏

本文介绍了一种验证哥德巴赫猜想的程序设计方法，通过寻找20亿以内偶数能够表示为两个素数之和的有效算法。利用Python语言实现了素数检测，并通过优化素数查找范围解决了超时问题。

分析

首先根据输入数据，得到其素数列表。从第一个素数位置开始判断，如果N-该素数仍在素数列表里，
借鉴多方内容后，计算素数遇到超时问题：对检索范围划分int(n**0.5+1)和n//2+1。

题目

数学领域著名的“哥德巴赫猜想”的大致意思是：任何一个大于2的偶数总能表示为两个素数之和。比如：24=5+19，其中5和19都是素数。本实验的任务是设计一个程序，验证20亿以内的偶数都可以分解成两个素数之和。

解法：

n=int(input())
lst=[]
for i in range(2,n):
    flag=0
    for j in range(2,i):
        if i%j==0:
            flag=1
    if flag==0:
        lst.append(i)
for i in range(len(lst)):
    if n-lst[i] in lst:
        print("{} = {} + {}".format(n,lst[i],n-lst[i]))
        break

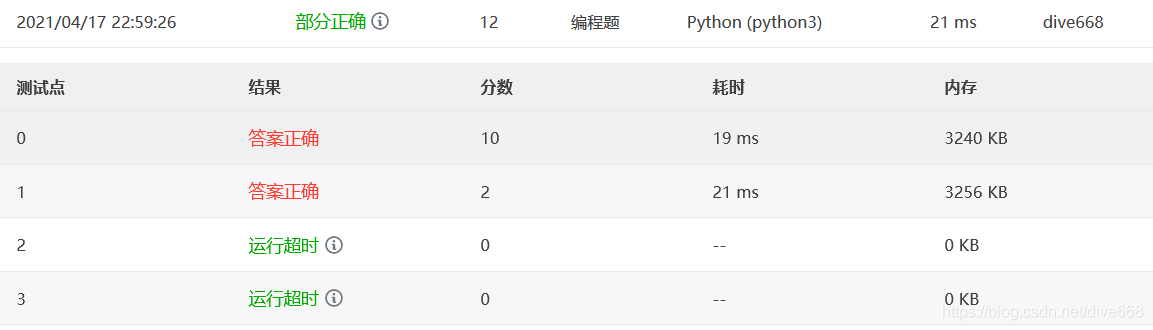
在这里插入图片描述

修改下，调用函数

函数用法是

#函数定义
def funname(argv[1]):
	details
#函数调用
funname(argv[2])

在这里插入图片描述

def is_sushu(n):
    for i in range(2,n):
        if n%i==0:
            return 0
    return 1
n=int(input())
for i in range(2,n):
    if is_sushu(i)==1 and is_sushu(n-i)==1:
        print("{} = {} + {}".format(n,i,n-i))
        break

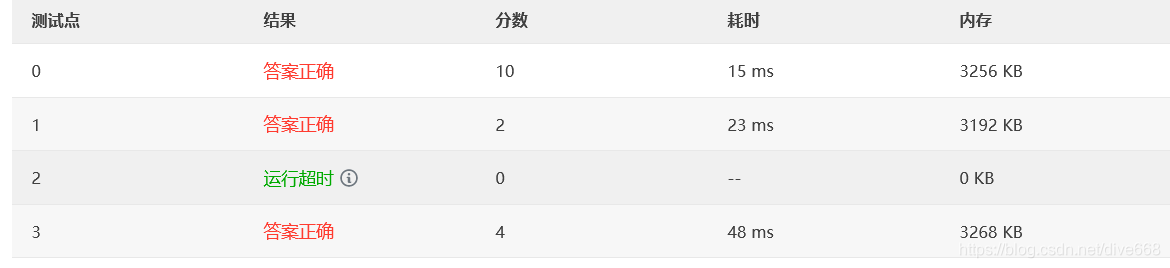
查找资料

查找素数范围在[2,√n]范围内，就不会超时。这里修改下range()范围，从2到int(n**0.5+1)。
另外运用：python // 与 / 的含义
" / “就表示浮点数除法，返回浮点结果;” // "表示整数除法。

def is_sushu(n):
    for i in range(2,int(n**0.5+1)):
        if n%i==0:
            return 0
    return 1
n=int(input())
for i in range(2,n//2+1):
    if is_sushu(i)==1 and is_sushu(n-i)==1:
        print("{} = {} + {}".format(n,i,n-i))
        break