【火炉炼AI】机器学习010-用朴素贝叶斯分类器解决多分类问题

【火炉炼AI】机器学习010-用朴素贝叶斯分类器解决多分类问题

【本文所使用的Python库和版本号】: Python 3.5, Numpy 1.14, scikit-learn 0.19, matplotlib 2.2

 

前面讲到了使用逻辑回归分类器解决多分类问题（【火炉炼AI】机器学习009-用逻辑回归分类器解决多分类问题 ），但是解决多分类问题并不是只有逻辑回归一种方法，此处我们讲解用朴素贝叶斯分类器来解决多分类问题。

朴素贝叶斯的“朴素”，并不是简单的意思，而是指样本的特征之间是相互独立的。在所有的机器学习分类算法中，朴素贝叶斯和其他绝大部分分类算法都不同，其他分类算法基本都是判别方法，即直接学习出特征输出Y和特征向量X之间的关系，要么是决策函数Y=f(X)，要么是条件分布P(Y|X)，但是朴素贝叶斯却是生成方法，也就是直接找出特征输出Y和特征向量X之间的联合分布P(X,Y)，然后用P(Y|X)=P(X,Y)/P(X)得出。

朴素贝叶斯的优点在于：1，有稳定的分类效率，2，对小规模数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，可以一批一批的去增量训练。3，对缺失数据不太敏感，算法比较简单，常用于文本分类。

但朴素贝叶斯的缺点是：1，朴素贝叶斯算法有一个重要的使用前提：样本的特征属性之间是相互独立的，这使得朴素贝叶斯算法在满足这一条件的数据集上效果非常好，而不满足独立性条件的数据集上，效果欠佳。理论上，朴素贝叶斯模型与其他分类方法相比，有最小的误差率，但是这一结果仅限于满足独立性条件的数据集上。在实际应用中，属性之间不太可能完全独立，特别是在特征属性个数非常多，且属性之间相关性较大时，朴素贝叶斯分类效果不太好。2，需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。3，由于通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。4，对输入数据的表达形式很敏感。

关于朴素贝叶斯模型的数学推导，可以参考：https://blog.youkuaiyun.com/malele4th/article/details/79348473

 

1. 准备数据集

本项目所使用的数据集参考《Python机器学习经典实例》中第二章提供的data_multivar数据集，下面是加载并分析该数据集的代码。

# 准备数据集  
data_path='D:\PyProjects\DataSet/NaiveBayers/data_multivar.txt'  
df=pd.read_csv(data_path,header=None)  
# print(df.head())  
# print(df.info()) # 查看数据信息，确保没有错误  
dataset_X,dataset_y=df.iloc[:,:-1],df.iloc[:,-1] # 拆分为X和Y  
# print(dataset_X.head())  
# print(dataset_X.info())  
# print('-'*100)  
# print(dataset_y.head())  
dataset_X=dataset_X.values  
dataset_y=dataset_y.values  
# print(dataset_X.shape) # (400, 2)  
# print(dataset_y.shape) # (400,)  
classes=list(set(dataset_y))   
print('class Num: {}, class: {}'.format(len(classes), classes))  
# 上面检查加载没有问题，一共有四个不同类别，类别名称为：0,1,2,3  

class Num: 4, class: [0, 1, 2, 3]

 

上面从txt文件中加载了数据集，可以看出，该数据集含有400个样本，被平均分成4个不同类别（0,1,2,3）。下面将这不同类别的数据集绘制到散点图中，以观察每个类别的大概聚集位置。

# 数据集可视化  
def visual_2D_dataset(dataset_X,dataset_y):  
    '''将二维数据集dataset_X和对应的类别dataset_y显示在散点图中'''  
    assert dataset_X.shape[1]==2,'only support dataset with 2 features'  
    plt.figure()  
    classes=list(set(dataset_y))   
    markers=['.',',','o','v','^','<','>','1','2','3','4','8'  
             ,'s','p','*','h','H','+','x','D','d','|']  
    colors=['b','c','g','k','m','w','r','y']  
    for class_id in classes:  
        one_class=np.array([feature for (feature,label) in   
                   zip(dataset_X,dataset_y) if label==class_id])  
        plt.scatter(one_class[:,0],one_class[:,1],marker=np.random.choice(markers,1)[0],  
                    c=np.random.choice(colors,1)[0],label='class_'+str(class_id))  
    plt.legend()  
  
visual_2D_dataset(dataset_X,dataset_y)  

 

 

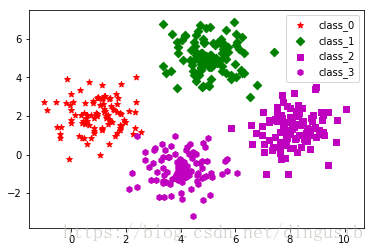
小结：

1，数据集的准备，分析，可视化等常常是机器学习的第一步，也是非常重要的一个部分，更是非常耗时的一个部分。

2，此处定义了一个数据集可视化函数，用于将具有两个特征属性的数据集按照不同类别绘制到散点图中。

 

2. 构建朴素贝叶斯分类器模型

在sklearn模块中，一共有三个朴素贝叶斯分类方法，分别是GaussianNB, MultinomialNB和BernouliNB，其中，GaussianNB是先验为高斯分布的朴素贝叶斯，适用于样本特征的分布大部分是连续值的情况；MultinomialNB是先验为多项式分布的朴素贝叶斯，适用于样本特征的分布大部分是多元离散值的情况；BernouliNB是先验为伯努利分布的朴素贝叶斯，适用于样本特征是二元离散值或者很稀疏的多元离散值的情况。下面我分别用这三个分类方法来解决本项目的分类问题。

 

2.1 使用GaussianNB分类器构建朴素贝叶斯模型

    直接上代码，构建模型后还测试了一下该模型在整个数据集上的表现：

# 使用GaussianNB分类器构建朴素贝叶斯模型  
from sklearn.naive_bayes import GaussianNB  
gaussianNB=GaussianNB()  
gaussianNB.fit(dataset_X,dataset_y)  
  
# 评估本模型在整个数据集上的表现  
dataset_predict_y=gaussianNB.predict(dataset_X)  
correct_predicts=(dataset_predict_y==dataset_y).sum()  
accuracy=100*correct_predicts/dataset_y.shape[0]  
print('GaussianNB, correct prediction num: {}, accuracy: {:.2f}%'  
      .format(correct_predicts,accuracy))  
  
plot_classifier(gaussianNB,dataset_X,dataset_y)  

correct prediction num: 398, accuracy: 99.50%

 

 

2.2 使用MultinomialNB分类器构建朴素贝叶斯模型

很可惜，貌似MultinomialNB分类器要求数据集的所有特征属性都是非负数，否则没法训练。故而下面的代码报错。

# 使用MultinomialNB分类器构建朴素贝叶斯模型  
from sklearn.naive_bayes import MultinomialNB  
multinomialNB=MultinomialNB()  
multinomialNB.fit(dataset_X,dataset_y)   
# 此处报错，multinomialNB的数据集的特征属性必须是非负数  
  
# 评估本模型在整个数据集上的表现  
dataset_predict_y_multi=multinomialNB.predict(dataset_X)  
correct_predicts_multi=(dataset_predict_y_multi==dataset_y).sum()  
accuracy=100*correct_predicts_multi/dataset_y.shape[0]  
print('MultinomialNB, correct prediction num: {}, accuracy: {:.2f}%'  
      .format(correct_predicts,accuracy))  

ValueError: Input X must be non-negative

 

2.3 使用BernouliNB分类器构建朴素贝叶斯模型

构建和测试方法与GaussianNB几乎一样，代码为：

# 使用BernouliNB分类器构建朴素贝叶斯模型  
from sklearn.naive_bayes import BernoulliNB  
bernoulliNB=BernoulliNB()  
bernoulliNB.fit(dataset_X,dataset_y)   
  
# 评估本模型在整个数据集上的表现  
dataset_predict_y_bern=bernoulliNB.predict(dataset_X)  
correct_predicts_bern=(dataset_predict_y_bern==dataset_y).sum()  
accuracy=100*correct_predicts_bern/dataset_y.shape[0]  
print('BernoulliNB, correct prediction num: {}, accuracy: {:.2f}%'  
      .format(correct_predicts_bern,accuracy))  
  
plot_classifier(bernoulliNB,dataset_X,dataset_y)  

BernoulliNB, correct prediction num: 195, accuracy: 48.75%

 

 

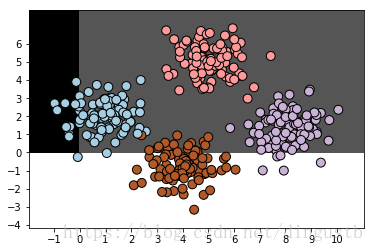
小结：

1，虽然sklearn模块中有三种朴素贝叶斯方法，但在同一个数据集上的表现却大不相同，只有GaussianNB表现最好，能够正确的将四个数据集区分开来。

2，此处定义了一个数据集可视化函数，用于将具有两个特征属性的数据集按照不同类别绘制到散点图中，对于其他项目这个函数也可以直接使用。

3，这三种朴素贝叶斯方法中，MultinomialNB要求数据集中的特征向量数值必须为非负数，否则直接报错。BernoulliNB虽然没有报错，但是从分类结果图中可以看到，结果非常不理想，可以说完全没有起到分类的效果。

 

注：本部分代码已经全部上传到（我的github）上，欢迎下载。

 

参考：Python机器学习经典实例，Prateek Joshi著，陶俊杰，陈小莉译