MIT6_0002F16_ProblemSet4

最新推荐文章于 2019-10-12 16:32:58 发布

原创最新推荐文章于 2019-10-12 16:32:58 发布 · 516 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#MIT6_0002F16_ProblemSet4 #MIT6_0002F16_ProblemSet #MITpython

MIT python课程作业专栏收录该内容

9 篇文章

订阅专栏

这篇博客详细介绍了MIT6_0002F16_ProblemSet4实验，涉及设计并实现一个细菌种群动态模拟，包括无抗生素和有抗生素的情况。实验通过模拟分析了不同治疗方案对细菌传播的影响，观察了抗生素使用前后细菌数量和耐药菌群体的变化。

MIT6_0002F16_ProblemSet4

实验内容：

本次实验旨在设计并实现一个细菌种群动态的随机模拟模型，并根据模拟结果得出各种治疗方案如何影响细菌的传播的结论。

实验流程：

阅读实验pdf，可知实验具体要求，按照要求一步一步解决。

Problem 1: Implementing a Simple Simulation

该部分为最简易的细菌模拟，不添加抗生素，简单模拟细菌的种群增长情况。

主要任务是填写 SimpleBacteria类和Patient类。SimpleBacteria 类表示单个细菌的状态。Patient维护与病人相关的细菌种群的状态。

代码如下:(根据提示较易完成)

class SimpleBacteria(object):
    def __init__(self, birth_prob, death_prob):
        #max出生概率
        self.birth_prob=birth_prob
        #max死亡概率
        self.death_prob=death_prob

    def is_killed(self):
        #利用随机的办法判断是否死亡
        return random.random() <= self.death_prob 

    def reproduce(self, pop_density):
        #利用随机的办法判断是否将繁殖，繁殖可能性为self.birth_prob * (1 - pop_density).
        if random.random() < (self.birth_prob * (1 - pop_density)):
            return SimpleBacteria(self.birth_prob, self.death_prob)
        else:
            raise NoChildException

class Patient(object):
    def __init__(self, bacteria, max_pop):
        #病人身上的细菌
        self.bacteria=bacteria
        #最大的细菌种群大小
        self.max_pop=max_pop
    def get_total_pop(self):
        #返回细菌数目
        return len(self.bacteria)
    def update(self):
        #根据提示即可完成
        #判断一下细菌是否死亡或者产生新的细菌
        surviving_bacteria = []
        for bacterium in self.bacteria:
            if not bacterium.is_killed():
                surviving_bacteria.append(bacterium) 
        #计算当前种群密度，用细菌数/菌落数 
        pop_density = len(surviving_bacteria) / self.max_pop
        #判断存活细菌是否将产生新细菌
        child_bacteria = []
        for bacterium in surviving_bacteria:
            try:
                child_bacteria.append(bacterium.reproduce(pop_density))
            except NoChildException:
                pass
        self.bacteria = surviving_bacteria + child_bacteria
        return len(self.bacteria)

Problem 2: Running and Analyzing a Simple Simulation (No Antibiotic Treatment)

模拟没有抗生素的情况下细菌的生长情况。需要完成两个函数：simulation_without_antibiotic 以及calc_pop_avg，calc_pop_avg用来求第n个时间点的细菌平均数，simulation_without_antibiotic 用来模拟细菌的生长情况。完成代码后，运行populations = simulation_without_antibiotic(100, 1000, 0.1, 0.025, 50) 可得具体生长图像。populations 是一个二维list，用于存取每个菌落与时间相关的性质，每个list元素中的元素表示一个菌落随时间step的变化

代码：

#返回第n步的细菌平均数
def calc_pop_avg(populations, n):   
    data=[]
    #取每个菌落的第n步的菌落数
    for i in range(len(populations)):
        data.append(populations[i][n])
    #返回其平均值即可
    return np.mean(data)
def simulation_without_antibiotic(num_bacteria,max_pop,birth_prob,death_prob,num_trials):
    #题目的图中steps达到了300，故这里选取300
    time_steps = 300
    populations = []
    #模拟num_trials个菌落的生存情况，并将具体数据记录
    for trial_i in range(num_trials):
        bacteria = [SimpleBacteria(birth_prob,death_prob) for i in range(num_bacteria)]
        patient = Patient(bacteria, max_pop)
        trial_data = [patient.get_total_pop()]
        for time_step in range(time_steps-1):
            trial_data.append(patient.update())
		#模拟每个菌落n步后，将该list加入到population中
        populations.append(trial_data) 

    # 画图
    x_coords = list(range(time_steps))
    y_coords = [calc_pop_avg(populations, n) for n in x_coords]
    make_one_curve_plot(x_coords, y_coords, "Time Step", "Avg. Population", "Uninhibited Bacterial Growth")
    #返回该二维list
    return populations

运行结果：符合预期

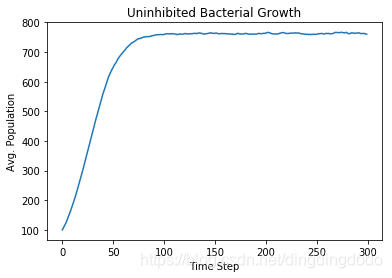
test函数也说明函数正确：

`test_calc_pop_avg (__main__.ps4_calc) ... ok`

Problem 3: Calculating a Confidence Interval

这一部分我们需要以问题2模拟中收集到的数据为样本，构建一个95%置信区间，估计在某个时间步长(零索引)下的平均细菌数量。根据数学公式提示较易完成：

def calc_pop_std(populations, t):
    #将第t步的数据记录
    data = [populations[i][t] for i in range(len(populations))] 
    #调用库返回std
    return np.std(data)

def calc_95_ci(populations, t):
    #平均数
    mean = calc_pop_avg 
    #根据公式求1.96*SEM
    width = calc_pop_std(populations, t)/(len(populations)**0.5) * 1.96
    #返回mean+-SEM
    return (mean, width)

运行test函数：

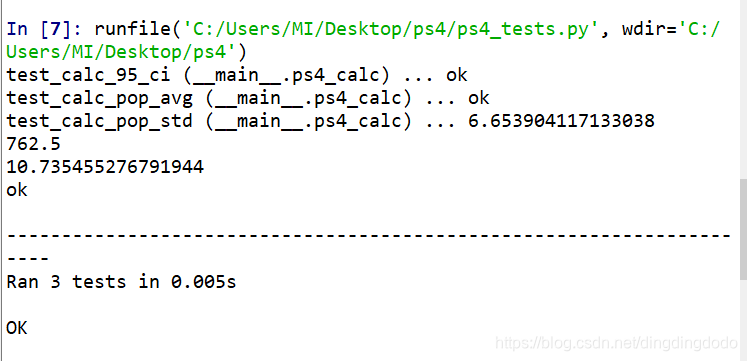
利用上述给的population，运行calc_95_ci(populations,299)并打印结果，如下：

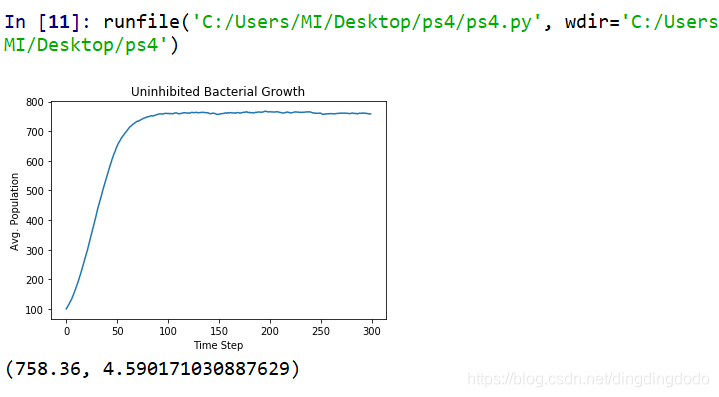
Problem 4: Implementing a Simulation with an Antibiotic

这部分填写ResistantBacteria 抗药性细菌类，是SimpleBacteria 的一个子类。

耐药性细菌有特殊的性质，对抗生素耐药的细菌死亡率固定，没抗生素耐药的细菌死亡率为death_prob/4。

class ResistantBacteria(SimpleBacteria):
    def __init__(self, birth_prob, death_prob, resistant, mut_prob):
        #调用父类初始函数
        SimpleBacteria.__init__(self,birth_prob,death_prob)
        #细菌突变概率，后代获得抗药性的概率
        self.mut_prob = mut_prob
        #是否是抗药性
        self.resistant=resistant

    def get_resistant(self):
        return self.resistant

    def is_killed(self):
        #如果是抗药性的话，以故定概率死亡
        if self.get_resistant():
            return random.random() < self.death_prob
        #否则以death_prob/4概率死亡
        else:
            return random.random() < self.death_prob/4

    def reproduce(self, pop_density):
         #判断是否可以繁殖
         if random.random() < (self.birth_prob * (1 - pop_density)):
            #父代有抗药性，则子代具有抗药性
            if self.get_resistant():
                return ResistantBacteria(self.birth_prob, self.death_prob,
                        self.resistant, self.mut_prob)
            #父代有抗药性，子代有可能有抗药性
            elif random.random() < (self.mut_prob * (1 - pop_density)):
                return ResistantBacteria(self.birth_prob, self.death_prob,
                        True, self.mut_prob)
            #子代没有抗药性  
            else:
                return ResistantBacteria(self.birth_prob, self.death_prob,
                        False, self.mut_prob)

TreatedPatient 类，是Patient的子类，表示接受抗生素的病人。

class TreatedPatient(Patient):
    def __init__(self, bacteria, max_pop):
        #调用父类构造函数
        Patient.__init__(self, bacteria, max_pop)
        #默认为未注射抗生素
        self.on_antibiotic = False

    def set_on_antibiotic(self):
        #注射抗生素
        self.on_antibiotic = True

    def get_resist_pop(self):
        #返回细胞数
        counter = 0
        for bacterium in self.bacteria:
            if bacterium.get_resistant():
                counter += 1
        return counter

    def update(self):
         #判断一下细菌是否死亡
        surviving_bacteria = []
        for bacterium in self.bacteria:
            if not bacterium.is_killed():
                surviving_bacteria.append(bacterium) 
        #判断在有抗生素情况下细菌生存情况
        if self.on_antibiotic:
            surviving_bacteria = [bacterium for bacterium in 
                    surviving_bacteria if bacterium.get_resistant()]
        #细菌繁殖情况
        pop_density = len(surviving_bacteria) / self.max_pop
        child_bacteria = []
        for bacterium in surviving_bacteria:
                child_bacteria.append(bacterium.reproduce(pop_density))
        #总细菌数目=没死的细菌加上繁殖的细菌       
        self.bacteria = surviving_bacteria + child_bacteria
        return len(self.bacteria)

Problem 5: Running and Analyzing a Simulation with an Antibiotic

该部分用于模拟研究耐药细菌以及抗生素治疗的效果。

def simulation_with_antibiotic(num_bacteria,max_pop,birth_prob,death_prob,
                               resistant, mut_prob,num_trials):
    #根据注释确定需要的变量
    time_steps_before_antibiotic = 150
    time_steps_after_antibiotic = 250
    populations = []
    resistant_pop = []

    #每过一个时间片
    for trial_i in range(num_trials):
        #实例化相应的细菌以及病人
        bacteria = [ResistantBacteria(birth_prob, death_prob, resistant,
            mut_prob) for i in range(num_bacteria)]
        patient = TreatedPatient(bacteria, max_pop)

        trial_data = [patient.get_total_pop()]
        trial_data_resist = [patient.get_resist_pop()]

        # 加入抗生素治疗
        for time_step in range(time_steps_before_antibiotic - 1):
            trial_data.append(patient.update())
            trial_data_resist.append(patient.get_resist_pop())
        patient.set_on_antibiotic()

        for time_step in range(time_steps_after_antibiotic):
            trial_data.append(patient.update())
            trial_data_resist.append(patient.get_resist_pop())

        populations.append(trial_data) 
        resistant_pop.append(trial_data_resist)

    # 作图：
    x_coords=list(range(time_steps_before_antibiotic + time_steps_after_antibiotic))
    y_coords1 = [calc_pop_avg(populations, n) for n in x_coords]
    y_coords2 = [calc_pop_avg(resistant_pop, n) for n in x_coords]
    make_two_curve_plot(x_coords, y_coords1, y_coords2,
                        "Total",
                        "Resistant",
                        "Timestep",
                        "Avg. Population",
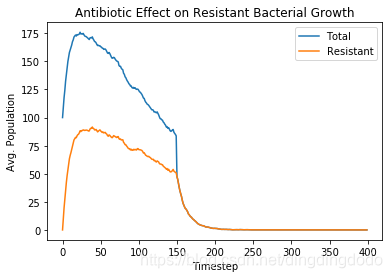
                        "Antibiotic Effect on Resistant Bacterial Growth")

    return （populations, resistant_pop）

运行结果：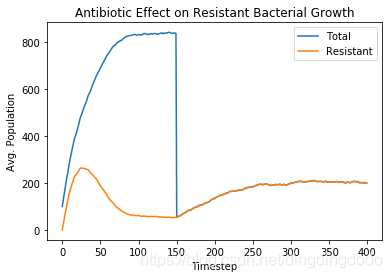

运行程序找对应的置信区间：
4个置信区间：

(196.8, 7.437677056716028)
(196.8, 7.437677056716028)
(0.0, 0.0)
(0.0, 0.0)

Problem 6 Write-up

A和B两种模拟只有一个区别，便是细菌的繁殖率，因此我们可以认为当繁殖率较低时在抗生素条件下很难维持增长，如果繁殖率较高，则随着突变的发生，产生突变的细菌也就越来越多，这样最终导致抗药菌很多，从而实现了增长。

What happens to the total population before introducing the antibiotic?

引入抗生素之前，细菌数量增长非常快。
What happens to the resistant bacteria population before introducing the antibiotic?

耐药菌数目也是增长迅速，占总菌种一定比例。
What happens to the total population after introducing the antibiotic?

A情景引入抗生素后细菌数量迅速下降，但之后恢复。B场景中下降至0
What happens to the resistant bacteria population after introducing the antibiotic?

在A情景下引入抗生素菌下降后又开始上升，而B情景则下降至0