基于深度生成模型的半监督网络流量分类

写在前面：
本文翻译供个人研究学习之用，不保证严谨与准确
github链接：https://github.com/WithHades/network_traffic_classification_paper
本文原文：Li, T., Chen, S., Yao, Z., Chen, X., & Yang, J. (2018). Semi-supervised network traffic classification using deep generative models. 2018 14th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), 1282–1288.

基于深度生成模型的半监督网络流量分类

摘要
  网络流量分类在网络管理和安全领域中起着基础性的作用。近年来，机器学习技术被用来对网络流量进行分类。特别半监督学习非常适合实际情况，在这种情况下，很难获得预先标记的训练流。提出了一种基于深度生成模型的半监督网络流量分类方法。具体来说，特征提取模块的目的是在低维特征空间中自动发现原始流量数据的表示特征。然后，利用这些表示特征，利用半监督分类模块训练分离分类器。通过异常检测层、协议层和应用层三个不同层次的数据集对该方法进行了验证。结果表明，该方案不仅可以检测恶意软件流量，而且可以根据恶意软件的协议、应用和攻击类型对流量进行分类。利用整个数据集不到20%的标记流，可以达到95%以上的准确率，与有监督学习方法相比是一个令人满意的值。

  关键词： 网络流量分类，半监督学习，深度生成网络，特征工程学习, 网络攻击检测

I. 介绍

  随着大数据时代的到来，新型的互联网应用应运而生，网络的构成也变得更加复杂。网络管理员应该了解更多关于网络流量的应用程序和协议的信息，以便更好地实现网络调度和攻击防御策略。近几十年来，基于用户行为分析的网络流量分类在优化网络配置、降低网络安全风险、提供更好的服务质量等方面具有不可或缺的价值，引起了人们的广泛关注[1]。
  有三类流量分类方法：基于端口的、基于深度包检查（DPI）的和基于流量统计的方法[1]。传统的基于端口的方法通过将数据包中的端口号映射到已知的应用程序来识别网络应用程序。但随着动态端口业务的增长和网络地址转换的采用，基于端口的分类变得不可靠。基于DPI的方法在IP包的有效负载中搜索应用程序的签名，这有助于避免动态端口问题[2]。目前，它是最实用的方法。然而，基于DPI的方法在处理加密流量时失败了。
  基于统计的方法没有通过匹配预定义的规则来执行流量分类，而是利用一组流量的可观察特征（例如，分组大小的均值和方差以及分组之间的间隔时间）来展示网络流量的不同行为和潜在特性。大多数基于统计的方法可以进一步分为有监督或无监督学习算法。一方面，监督学习主要利用机器学习的方法，从具有一组选择性特征的标记流中提取模式来学习流量分类器。然而，性能取决于在实践中很难获得的预标记流的质量和数量[3]。另一方面，无监督方法通过聚类技术（如Kmeans）对一组未标记流进行分类。然后，通过人工标注的方式，将聚类结果用于构建分类器。然而，准确度远不能令人满意。
  本文在深入生成模型和变分推理理论的基础上，利用密度模型提出了一种半监督网络流量分类方法。我们的方案只需要少量的标记流，但达到了令人满意的90%以上的精度。本文的主要贡献概括如下：

• 我们使用一个深度生成模型作为特征抽取器来提供原始流的表示特征。相关的流将被聚类到一个潜在的特征空间上，使得分类更加准确。
• 我们提出了一个半监督方案来解决只有少量标记流的流量分类问题。该方法结合了近年来在深生成模型和变分推理理论领域的成功结果。
• 我们在三个不同层次的网络流量数据集上进行了实验。结果表明，该方案不仅可以检测恶意软件流量，而且可以根据恶意软件的协议、应用和攻击类型对流量进行分类。

II. 相关工作

  基于端口和基于DPI的流量分类方法在实际应用中有着广泛的应用。Finsterbusch等人[6]综述了目前基于DPI的流量分类方法。相关工作主要集中在如何准确地确定映射规则，减少有效载荷检测的时间消耗，提高性能等方面。
  由于基于规则的方法面临着动态端口和加密流量的问题，近年来的研究主要集中在如何将基于流量统计的方法与机器学习技术结合起来。Nguyen和Armitage[2]对几种机器学习方法处理网络流量分类的性能进行了比较。在训练数据集完全标记的情况下，利用监督学习算法对分类器进行训练。例如，Naive Bayes[9]、支持向量机（SVM）[7]和决策树[8]已经使用选择性流特征对此问题进行了评估。随着人工智能（AI）的发展，除了上述传统的机器学习方法外，还应用了深度学习技术来构建分类器。Javaid等人[10]提出了一种基于稀疏自动编码器（SAE）的网络入侵检测方案。Wang等人[11]提出了一种基于一维卷积神经网络的加密流量分类方法。采用长-短期记忆网络（LSTM）[12]学习时间流特征，提高分类精度。
  一些无监督的学习方法，如K-均值[13]和期望最大化（EM）[14]被用来对流量进行自动聚类。乔纳斯等人[3]提出了一种基于神经自动编码器的无监督学习流量分类算法。半监督学习是一种将大量未标记流和少量标记流输入分类器的混合学习方法。Erman等人[13]首先在聚类过程中使用K-Means算法，然后利用标记流对聚类结果进行分类应用。
  在本文中，我们的方法也是半监督的，但它是一个端到端的分类模型，而不是一个单独的两步过程。标记流和未标记流用于同时训练模型，这比以前的“特征-簇-标签”方案更高效、更自动。同时，所选择的特征在反映流行为方面起着重要的作用。因此，我们没有使用手工制作的流程统计，例如[9]中提出的248个统计特征集，而是使用了先进的深生成模型。具体地说，变分自动编码器（VAE）[4]通过将原始流嵌入低维潜在特征空间来表示原始流的特征。

III. 半监督网络流量分类的深生成模型

  在这一部分中，我们提出了一个半监督方案来处理网络流量分类问题。该框架主要包括两个模块：特征提取模块和半监督分类模块。图1显示了整个框架。特征提取模块需要预先训练，目的是在无监督的情况下自动发现原始流的表示特征。然后，利用表示特征，利用半监督分类模块训练分离分类器。在该模块中，我们提出了一个概率模型来描述除了一些潜在变量之外，由特定的流量类型生成的流量。

图1 半监督流量分类框架

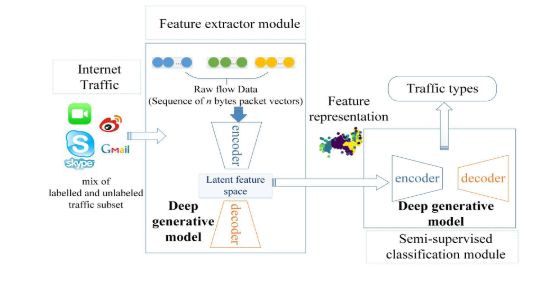
A. 特征提取

  使用变分自动编码器（VAE）学习原始流（n字节网络包序列）的表示特征。在图2中，使用VAE，我们可以获得低维空间中的表示特征。这些低维特征比原始流更容易分离，因为具有相似特征的流聚集在潜在特征空间上。我们将流量数据建模为对： ( x , y ) = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } (x, y) = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\} (x,y)={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，其中$x_i\in R^D$表示第i个原始流， y i ∈ { 1 , . . . , L } y_i \in \{1, ..., L\} yi​∈{1,...,L}是它的类标签。每个原始流$x_i$都有相应的表示特性$z_i$。

  如图2所示，我们将$q_{\varnothing }(z|x)$称为概率编码器，因为给定原始流x，它可以在表示特征z上产生后验分布，我们将其表示为“表示特征分布”。具体来说，我们用来推断表示特征的编码器是高斯网络：
$$q_{\varnothing }(z|x)=N(z|{\mu }_{\varnothing }(x),diag({\sigma }^2(x)))\text{\hspace{1em}(1)}$$
  编码器以深度神经网络的形式构造。这个表示分布的均值和方差$q_{\varnothing }(z|x)$是编码器的输出。这里，函数${\mu }_{\varnothing }(x)$，${\sigma }^2(x)$表示为多层感知器（MLPs）。
  我们还将$q_{\varnothing }(z|x)$称为概率解码器，因为给定流表示特性z，它会产生原始流x的可能值上的分布。我们用于重建流的解码器是：
$$p(z)=N(z|0,I);p_{\theta }(x|z)=f(x;z,\theta )\text{\hspace{1em}(2)}$$
  其中$f(x;z,\theta )$是一个是一个似然函数，其概率由参数$\theta$的深神经网络和一组表示特征z构成。
  变分自动编码器使我们能够通过推理网络$q_{\varnothing }(z|x)$获得每个原始流x的表示特征z。应该注意的是，这个程序是完全无监督的。

B. 半监督分类

  在半监督分类情况下，只有一小部分流具有已知的类标签。为了解决标签丢失的问题，我们提出了另一种生成模型，即VAE变形模型。该模型描述了由潜在类变量y和其他潜在变量$z^{{}^{\prime }}$生成的流。图3和图4显示了结构细节:

图3 标签数据的半监督分类模块

图4 未标记数据的半监督分类模块

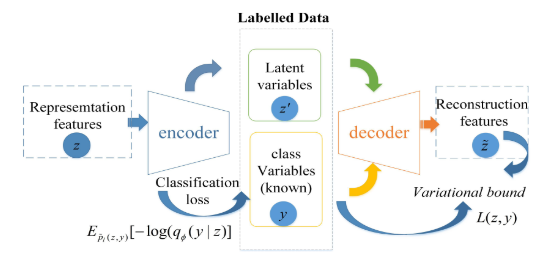
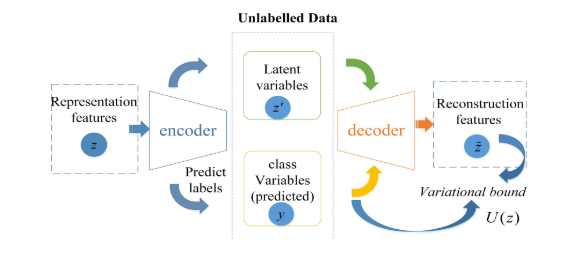
  分类被集成到推理过程中。与特征提取模块不同，对于分类模块中的编码器，我们使用高斯网络来推断潜在变量$z^{{}^{\prime }}$和y为：

$$q_{\varnothing }(z^{{}^{\prime }}|z)=N(z|{\mu }_{\varnothing }(z),diag({\sigma }^2(z)))$$
$$q_{\varnothing }(y|z)=Cat(y|{\pi }_{\varnothing }(z))\text{\hspace{1em}(3)}$$
  $Cat(y|\pi )$是多项式分布。如果之前没有流的类标签，则类标签y将被视为需要推断的潜在变量。函数${\mu }_{\varnothing }(z),{\sigma }^2(z),{\pi }_{\varnothing }(z)$表示为MLPs。我们用来重建特征的分类模块中的解码器是：

$$p(y)=Cat(y|\pi );p(z^{{}^{\prime }})=N(z^{{}^{\prime }}|0,I)$$
$$p_{\theta }(z^{{}^{\prime }}|y,z)=f(z;y,z^{{}^{\prime }},\theta )\text{\hspace{1em}(4)}$$
  同样的,$f(z;y,z^{{}^{\prime }},\theta )$是一个似然函数,其概率由参数$\theta$的深神经网络和潜在变量y和$z^{{}^{\prime }}$构成。
  现在可以使用推理网络$q_{\varnothing }(y|z)$作为分类器，从中我们可以得到任何缺少标签的流的预测。

C. 目标函数与优化

  对于特征提取模块，目标函数是VAE模型的变分界[4]，可以写成：
$$L(\theta ,\varnothing ;x^{(i)})=D_{KL}(q_{\varnothing }(z|x^{(i)})||p_{\theta }(z))+E_{q_{\varnothing }(z|x^{(i)})}[log{p}_{\theta }(x^{(i)}|z)]\text{\hspace{1em}(5)}$$
  对于半监督分类模块，我们有两种情况需要考虑[15]：
(1)考虑到标记流，如图3所示，变分边界是等式（5）的一个扩展：
$$\begin{gathered} L(z^{(i)},y) \\ =D_{KL}(q_{\varnothing }(z^{{}^{\prime }}|z^{(i)})||p_{\theta }(z^{{}^{\prime }}))+E_{q_{\varnothing }(z^{{}^{\prime }}|z^{(i)})}[log{p}_{\theta }(z^{(i)}|y,z^{{}^{\prime }})] \\ =E_{q_{\varnothing }(z^{{}^{\prime }}|z^{(i)},y)}[log{p}_{\theta }(z^{(i)}|y,z^{{}^{\prime }})+log{p}_{\theta }(z^{{}^{\prime }})+log{p}_{\theta }(y)-log{q}_{\varnothing }(z^{{}^{\prime }}|z^{(i)})]\text{\hspace{1em}(6)} \end{gathered}$$
(2)对于未标记的流，如图4所示，类标签y被视为分布上的一个潜在变量，因此带有未知标签的流的变化范围为:
$$\begin{gathered} U(z^{(i)}) \\ =D_{KL}(q_{\varnothing }(y,z^{{}^{\prime }}|z^{(i)})||p_{\theta }(z^{{}^{\prime }},y))+E_{q_{\varnothing }(y,z^{{}^{\prime }}|z^{(i)})}[log{p}_{\theta }(z^{(i)}|y,z^{{}^{\prime }})] \\ =\sum _y{q}_{\varnothing }(y|z^{(i)})(-L(z^{(i)},y))+H(q_{\varnothing }(y|z^{(i)}))\text{\hspace{1em}(7)} \end{gathered}$$
则整个数据集的变分界限为：

我们还添加了标记流的分类损失，总体目标函数是：

式（5）和式（9）分别为特征提取模块和半监督分类模块的优化提供了目标函数。利用随机梯度变分Bayes（SGVB）[5]方法，编码器和解码器的参数和都可以优化。 同样的计算策略可用于计算公式（9）的梯度。由于KL项可以解析计算，并且可以使用过程等式（11）估计重建误差项的梯度。

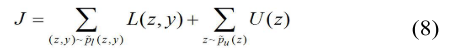
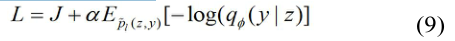
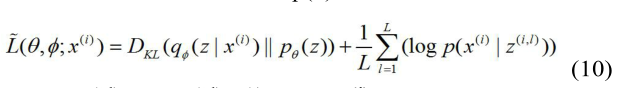
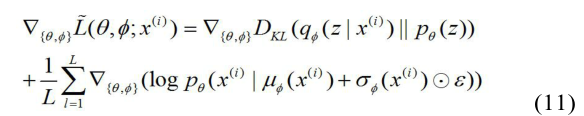
IV. 实验

  在这一部分中，我们在公共ISCxVPN流量数据集[16]和USTC-TFC2016数据集[17]上进行了各种实验，以评估所提出的半监督分类方法的性能。这些实验有以下目的：

• 评估特征提取模块的性能
    评估标记流的数量对半监督分类模块性能的影响；
    评估半监督分类方法在不同级别数据集上的性能：异常检测级别：检测来自网络流量的恶意软件流。协议级：根据协议类型对流进行分类；应用级：根据应用/攻击类型对流进行分类。

A. 实验实现

1. 数据集

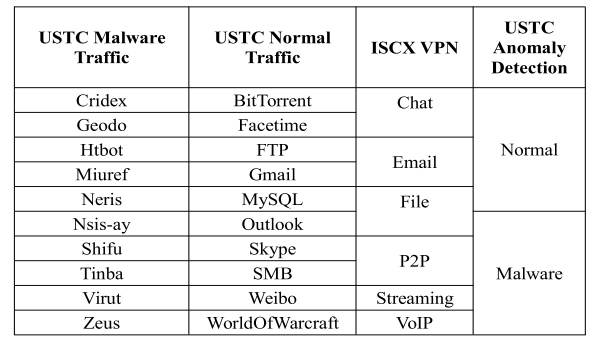
  目前大多数的公共流量数据都是基于流量统计的。但由于我们必须展示模型提取潜在流量特征的能力，因此我们选择以下三个包含原始流量数据而不是统计数据的数据集：
（1）ISCxVPN数据集：包括6种常规加密协议流量。
（2）USTC-TFC2016数据集：Wang等人[19]发布的数据集由两部分组成：恶意软件流量部分包含10种恶意软件流量；正常流量部分包含10种正常流量，由网络流量模拟设备采集。
（3）USTC异常检测数据集：为了进一步挖掘模型的异常检测能力，USTCTF2016中的每个流都根据其类型标记为正常或恶意软件，以构建2类数据集。
  四个数据集的流量组成见表1。

表1 数据集的流组成

B. 实验评估

1. 评价指标

  四个评价指标[2]被用来显示我们的方法的性能：精确性（A）、精确性（PR）、召回率（RC）和f1值（f1）。我们使用精确度来评估分类器的整体性能。另外三个指标（PR、RC、F1）被用来评价数据集中每一类的分类结果。利用上述指标，我们可以在训练后判断分类器的性能。

2. 实验结果
    A. 特征表示

图5 网络流的二维潜在特征

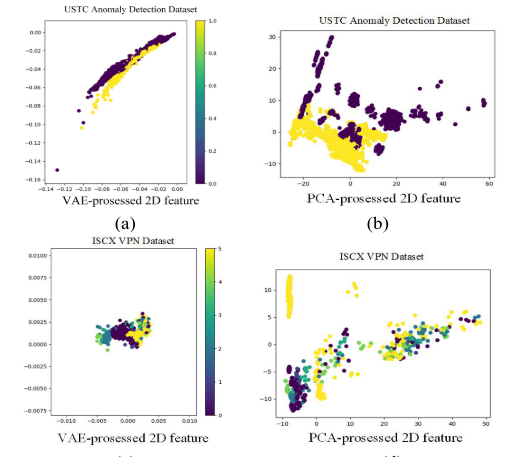
  图5中的（a）和（c）分别对应于USTC异常检测数据集和ISCxVPN数据集。它们显示了由基于VAE的特征提取模块获得的2D表示特征；（b）和（d）显示了通过对两个数据集执行PCA（主成分分析）方法获得的降维结果。与二维平面上的性能相比，VAE处理后的数据具有更好的聚类效果。这意味着同一类型的业务具有相似的内部特征，经过这种低维的嵌入后，原始业务流更容易在表示特征空间中分离。

    B. 半监督分类器性能

  首先，为了评估标记流对分类性能的影响，我们选择了不同数量的标记流，并比较了评价指标的变化趋势。我们将n_labels（每个流量类别的标记流量）设置为20、50、100、200，分别占USTC恶意软件流量数据集的0.31%、0.78%、1.56%和3.12%；USTC正常流量数据集的0.31%、0.77%、1.55%和3.10%；ISCX VPN数据集的1.77%、4.43%、10.0%和20%；USTC异常检测数据集的0.15%、0.39%、0.78%和1.56%。与传统的监督学习方法相比，该方法只使用最小标记流，通常将标记的训练集设置为整个数据集的70~80%。图6分别显示了四个数据集的不同n_labels的评估度量。我们还在表2中列出了USTC恶意软件流量数据集分类度量的具体值。

图6 四个数据集的度量值

表2 USTC恶意软件流量数据集的精度、召回率和F1值

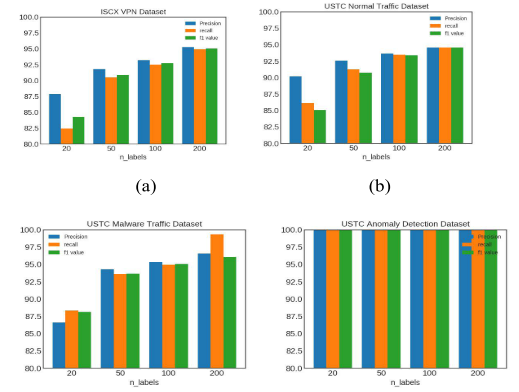
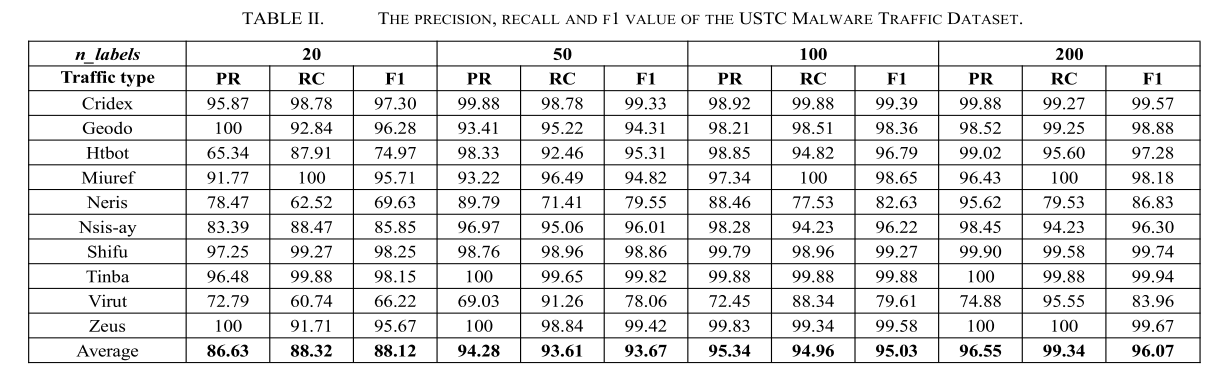
  如图6所示，虽然每个类只有20个标记流，但四个数据集的精度值都在85%以上，特别是USTC异常检测数据集的精度达到了100%。当标记流增加到每个类50时，四个数据集的精度、召回率和f1值都超过90%。当标签数量增加到每类200个时，度量值达到约95%。
  在四个数据集中，该方法对USTC异常检测数据集的性能最好（评价指标达到100%）。这意味着正常流和恶意流在流特性上有很大的差异，所以它们很容易被分离。在协议级和应用级分类方面，该方法的性能略有下降。可能的原因是，属于不同业务类别的应用程序可能具有一定程度的相似性，从而导致一些错误分类。例如，图7显示了USTC恶意软件流量数据集的混淆矩阵，每个类有50个标记流。对角线颜色的深度表示相应类别的分类精度。我们可以看到大多数的类都被准确地分类了，只有Neris和Virut的性能不能令人满意。

图7 USTC恶意软件数据集的混淆矩阵（n_labels=50）

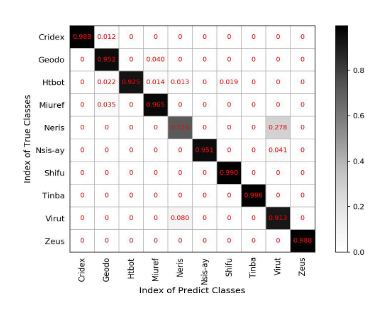
  图8显示了带有不同数量标记流的四个数据集的准确性。

图8 不同标记流的精度

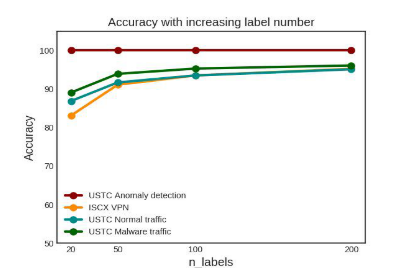
  我们可以看到，随着标记流的数量增加，精确度也在增加。具体来说，该方法在USTC异常检测数据集上的准确率最高，达到100%，整个数据集只有0.15%的标记流。在其他三个数据集上，每个类20个标记流的准确率达到80%以上，而50个标记流的准确率则提高到90%以上。对于每类200个标记流，与监督分类方法相比，准确率达到95%，是一个令人满意的值，但我们只使用了不到20%的整个数据集的标记流。与我们的方法类似，[3]使用神经自动编码器对流进行聚类，并从先前标记的数据中为该聚类分配最相似的标签。该方法的平均准确率为80%，召回率为75%，f1得分为76%。

V. 总结

  本文讨论了当整个数据集的标签无法获取时的网络流量分类问题。我们提出的方法去除了手工特征，但使用变分自动编码器以无监督的方式从原始流量中提取潜在特征。然后利用表示特征，将大量未标记流和少量标记流混合训练成基于深度生成模型的流量分类器。我们对四个不同级别的数据集进行了评估。
  在今后的工作中，还有一些问题需要进一步研究。首先，利用卷积神经网络（CNN）等深层学习技术来提高特征的表示能力和分类性能，并且，由于统计流特征被证明对网络分类有用，我们将把统计特征与原始的流量数据结合起来进行分类进一步探索。