【洛谷P1351】联合权值【树形DP】

$link$

分析：

树形$dp$
$f_{x,0/1}$表示$x$的子树内 与$x$距离为$0/1$点的最大权值
$g_{x,0/1}$表示$x$的子树内 与$x$距离为$0/1$点的权值和

相距$2$ 其实就是与$x$距离为$1$的两个点 产生的联合权值就是$f_{x,1}\times f_{to,0}$

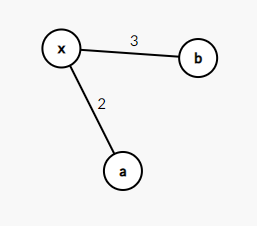
如图 $a,b$相距$2$ 就是与$x$相距$1$的$a,b$权值相乘了 权值和也同理 $g_{x,1}=g_{x,1}+g_{to,0}$
注意最大权值不用取$mod$
最后权值和要$\times 2$因为求出的 仅有无序的权值和

CODE：

#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e5+5,Mod=10007;
int n,head[N],tot,f[N][2],g[N][2],ans1,ans2,val[N];
struct node{
	int to,next;
}a[N<<1];
void add(int x,int y)
{
	a[++tot]=(node){y,head[x]};
	head[x]=tot;
}
void dfs(int x,int fa)
{
	f[x][0]=g[x][0]=val[x];
	for(int i=head[x];i;i=a[i].next)
	{
		int qwq=a[i].to;
		if(qwq==fa) continue;
		dfs(qwq,x);
		ans1=max(ans1,f[x][1]*f[qwq][0]);
		ans1=max(ans1,f[x][0]*f[qwq][1]);
		ans2=(ans2+g[x][1]*g[qwq][0]%Mod)%Mod;
		ans2=(ans2+g[x][0]*g[qwq][1]%Mod)%Mod;
		f[x][1]=max(f[x][1],f[qwq][0]);
		g[x][1]=(g[x][1]+g[qwq][0])%Mod;
	}
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);add(y,x);
	}
	for(int i=1;i<=n;i++)
		scanf("%d",&val[i]);
	dfs(1,0);
	printf("%d %d",ans1,(ans2<<1)%Mod);
	
	return 0;
}