Matlab（数值微积分）

原创

已于 2023-09-02 11:56:03 修改 · 2.3k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2023-09-02 11:53:47 首次发布

1.3.2 polyval() 多项式求值

1.3.3 polyder()多项式微分

1.4 多项式积分

1.4.1 如何正确表达

1.4.2 polyint() 多项式积分

3.4.2 integral2() 二级积分

3.4.3 integral3() 三级积分

1.多项式微分与积分

1.1 微分

函数f(x)导数写为：F'(x)或者 $\frac{df(x)}{dx}$
函数f(x)关于x的变化率

f (x0) 表示点x0处曲线相切的直线的系数。

1.2 多项式微分

对于一个多项式： $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$ 来说，其微分多项式为：

$f(x)=a_{n}nx^{n-1}+a_{n-1}(n-1)x^{n-2}+...+2a_{2}x+a_{1}$

1.3 如何正确的使用Matlab?

1.3.1 Matlab表达多项式

$f(x)=x^{3}-2x-5$

在上式中，我们用Matlab应该怎么进行表示（多项式在Matlab中被表示为行向量）

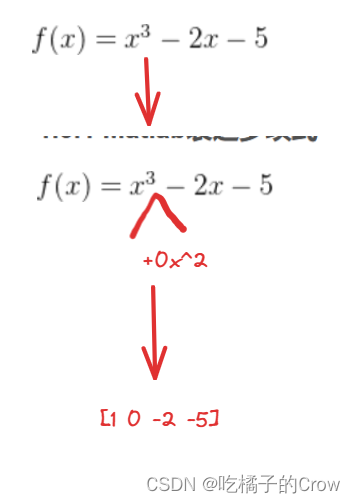
>> p=[1 0 -2 -5]

p =

     1     0    -2    -5

1.3.2 polyval() 多项式求值

语法：y=polyval(p,x)

y= polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）：

$p(x)=p_{1}x^{n}+p_{2}x^{n-1}+...+p_{n-1}x+p_{n}+1$

示例1：

计算多项式 p(x)=3x^2+2x+1在点 x=5、7 、9 处的值。

>> p = [3 2 1];
x = [5 7 9];
y = polyval(p,x)

y =

    86   162   262

示例2：

$f(x)=9x^{3}-5x^{2}+3x+7$ $(-2<=x<=5)$

对该多项式进行画图求值

>> a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f,'LineWidth', 2);%设置线条粗度
xlabel('x轴'); ylabel('f(x)');%设置xy轴名称
set(gca, 'FontSize', 14)%设置字体大小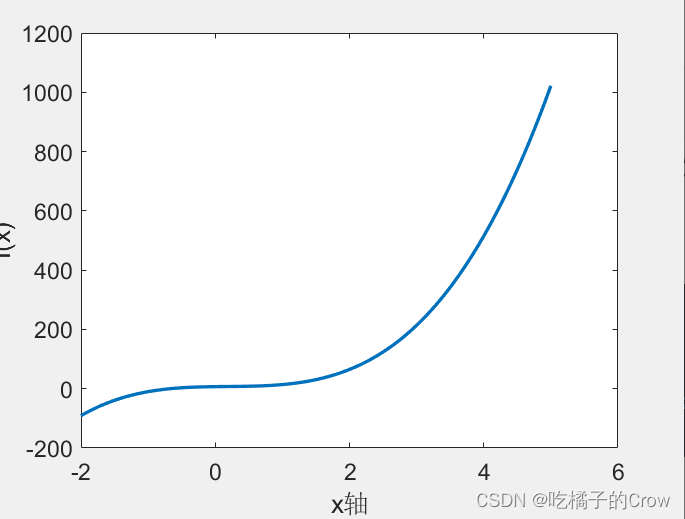

1.3.3 polyder()多项式微分

语法一：k=polyder(p)

k=polyder(p)返回的p中的系数表示的多项式的导数 $k(x)=\frac{d}{dx}p(x)$

示例：

创建一个向量来表示多项式 p(x)=3x^5−2x^3+x+5。

p = [3 0 -2 0 1 5];

使用polyder对多项式进行求导，结果为： $q(x)=15x^{4}-6x^{2}+1$

q = polyder(p)
q = 1×5

    15     0    -6     0     1

语法二：k= polyder(a,b) 返回多项式 a 和 b 的乘积的导数 $k(x)=\frac{d}{dx}[a(x)b(x)]$

示例：

创建两个向量来表示多项式 a(x)=x^4−2x^3+11 和 b(x)=x^2−10x+15。

a = [1 -2 0 0 11];
b = [1 -10 15];

q = polyder(a,b)
q = 1×6

     6   -60   140   -90    22  -110

最后的结果为:

语法三：[q,d] = polyder(a,b) 返回多项式 a 和 b 的商的导数

最低0.47元/天解锁文章