搜索--DFS--基础

简介

深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(n!)。

原理

为了求得问题的解，先选择某一种可能情况向前探索；
在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索；
如此反复进行，直至得到解或证明无解。

操作

不断向前搜索，若满足则输出，不满足，向后回溯，再向下一个元素点搜索

应用

842. 排列数字

题目

分析

一维枚举

本题，就相当于枚举每一个结果，从第一个位置到最后一个位置，首先想到DFS，因为dfs另一个含义就是爆搜，本题想到每一元素只能选一个，所以枚举每一个位置的元素可能是谁，依次向后拓展搜索，当超过了总位置数，则打印结果，否则继续拓展。

代码

#include <iostream>

using namespace std;

const int N = 10;

int n;

int q[N];
bool st[N];

void dfs(int u)
{
    if(u > n)
    {
        for(int i = 1; i <= n; i ++) printf("%d ", q[i]);
        puts("");
    }
    
    // 遍历每一个剩余的数字
    for(int i = 1; i <= n; i ++)
    {
        if(!st[i])
        {
            // 在第u位置上使用i 
            q[u] = i;
            st[i] = true;
            
            //搜索下一个位置 
            dfs(u + 1);
            
            // 恢复现场
            st[i] = false;
            q[u] = 0;
            
        }
    }    
}


int main()
{
    scanf("%d", &n);
    
    dfs(1);
    
    return 0;
}

843. n-皇后问题

题目

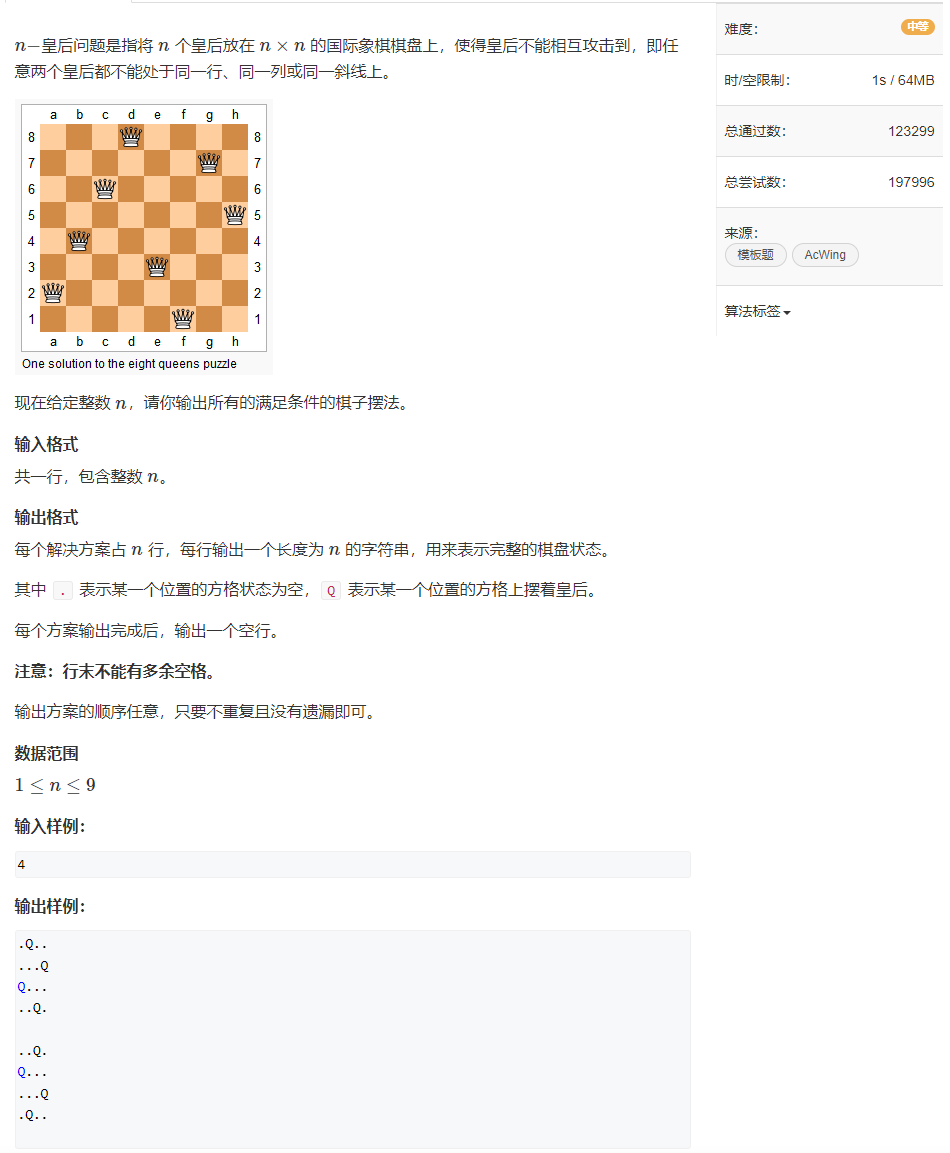
分析

二维枚举

本题，就相当于枚举每一个结果，从第一行到最后一行，首先想到DFS，因为dfs另一个含义就是爆搜，本题想到每一行只能选一个，所以枚举第一行的每一个列元素，依次向下行拓展搜索，当超过了总行数，则打印矩阵，否则继续拓展。

代码

// n-皇后问题
#include <iostream>
#include <cstring>
#include <stdio.h>


using namespace std;

const int N = 15;

int n;
char g[N][N];
bool col[N], dg[2 * N + 1], udg[2 * N + 1];

void dfs(int u)
{
	// 遍历到最后一行 
	if(u > n)
	{
		// 初始化棋盘
    	for(int i = 1; i <= n;  i ++)
    	{
    		for(int j = 1; j <= n; j ++)
    		{
    		  //  g[i][j] = '.'; 
    		    printf("%c", g[i][j]);
    		}
    		
    		printf("\n");
        }
        cout << endl;
	}
	
	// 当前行 
	int x = u;
	
	// 枚举当前行的每一个列元素 
	for(int i = 1; i <= n; i ++)
	{
		if(col[i] != true && udg[i + u] != true && dg[i - u + n] != true)
		{
			// 使用当前位置 
			col[i] = udg[i + u] = dg[i - u + n] = true;
			g[u][i] = 'Q';
			// 搜索下一行 
            dfs(u + 1);
            // 恢复现场 
            col[i] = udg[i + u] = dg[i - u + n] = false;
            g[u][i] = '.';
		}
	}
}



int main()
{
	cin >> n;

	
	// 初始化棋盘
	for(int i = 1; i <= n;  i ++)
		for(int j = 1; j <= n; j ++)
		{
		    g[i][j] = '.'; 
		  //  printf("%c", g[i][j]);
		}
		
	dfs(1);
	
	return 0;
}