【元学习】reptile数学推导

最新推荐文章于 2025-07-20 22:41:22 发布

转载最新推荐文章于 2025-07-20 22:41:22 发布 · 783 阅读

2 ·

CC 4.0 BY-SA版权

原文链接：https://zhuanlan.zhihu.com/p/103661664

算法专栏收录该内容

19 篇文章

订阅专栏

文章提供两个有关 reptile 工作过程的解释：

leading order expansion of the update

这部分我们会使用泰勒展开去近似 reptile 和 MAML 的更新过程。接下来我们将会看到两种算法都包括同样的两个组成部分：第一项负责最小化期望损失，第二项负责最大化任务内的泛化，具体来讲就是如果来自不同 batch 的梯度的点积为正值，那么在这个 batch 的表现提高同样也会提高另一个 batch 的表现，否则一个提高一个下降最后的结果就会为负，这样就变相的相当于是提高了针对给定任务的学习速度。这两项类似于我们在开头提到的MAML 的两次求导，第一次求导是针对各个任务分别进行参数更新，第二次求导是针对模型总的损失函数的求导，目的就是使得模型对各个任务都有较好的效果，又不会过于偏向于某个特定任务。

不同于 MAML 中的分析方法，这里不再区分训练集和测试集，仅仅假设每个任务提供 k 个损失值 $L_{1,...,k}$ ，例如：基于不同 minibatches 的分类损失。

推导过程中使用如下定义：

首先计算 SGD 梯度：

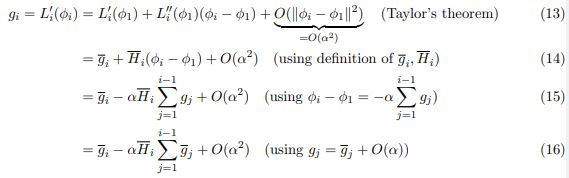
接下来，计算 MAML 梯度。定义 $U_{i}$ 为更新参数向量的操作：

$U_{i}(\phi )=\phi-\alpha L_{i}^{'}(\phi )$

将其展开：

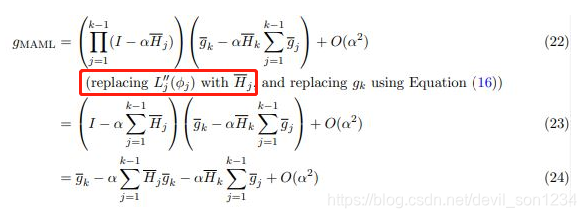
为了方便说明，考虑 k=2 的情况：

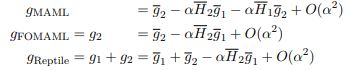
第一项就是直接套公式（24）；第二个公式 FOMAML 只考虑最后的一步梯度，即公式（16）；第三个公式就直接套 FOMAML 和（24）公式得到。

当基于 minibatch 抽样对各个 batches 的梯度取期望的时候，也就是内部的各个 minibathces 得到各自的梯度之后，要以什么样的方式反馈给外部一个总的结果，这里是取期望也就是一种平均计算。计算之后有两部分会被剩下，称其为 AvgGrad & AvgGradInner。

下面的推导会涉及的符号：

$E_{\tau ,1,2[...]}$

表示基于任务 $\tau$ 的 minibatches 取期望，两个 minibatch 分别定义了 $L_{1},L_{2}$ ：

AvgGrad：

AvgGradInner：

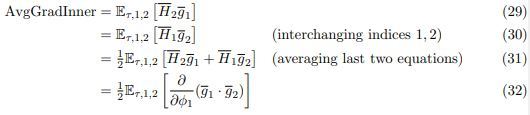
总的来说，第一个平均梯度的作用是减少总体任务的损失（取负值 -AvgGrad），第二个平均内部梯度的作用是增加给定任务的不同 minibatch 的梯度的内部点积，进而提高任务内的泛化能力（因为只有不同的梯度方向近似的时候点积结果才会更大，期望也才会更大）。

最终得到下面的 meta-gradient 的表示，对于 k=2 的随机梯度下降损失：

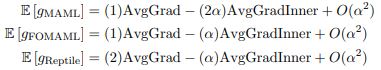
所以实际就是，上述的三个梯度表示都是首先使得任务的期望损失最小化，之后更高阶的 AvgGradInner 通过最大化给定任务的内部点积加速学习进程。

最后，还可以将 k =2 的情形扩展：

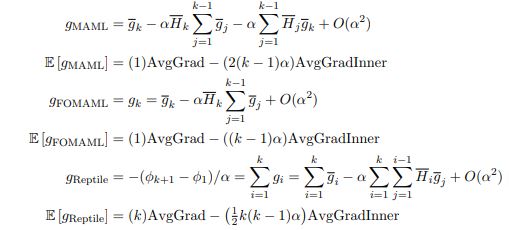
可以看到三者AvgGradInner与AvgGrad之间的系数比的关系是：MAML > FOMAML > Retile。这里作者并没有针对这个系数对模型具体有什么影响做进一步的讨论，我们可以看到这个比例与步长α，迭代次数k 正相关。注意上述推导利用的泰勒展开只有在αk 很小时才成立。

2. finding a point near all solution manifolds

第二种解释是假设 reptile 收敛于解 $\phi$ ，这个解在欧式空间靠近每个任务最优解的曲线，这样才能更快的让每个任务实现收敛。让 $\phi$ 定义为网络的初始化， $W_{\tau }$ 定义为任务 $\tau$ 的最优参数集，我们的目标就是找到一个 $\phi$ ，对于所有任务来说距离 $D(\phi ,W_{\tau })$ 都很小：

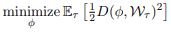
期望的梯度为：

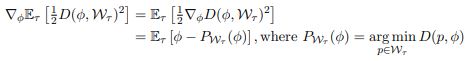
每次 reptile 的迭代，都是抽样一个任务 $\tau$ ，执行一次随机梯度下降：

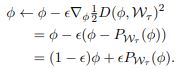
实际应用中，我们不能准确的计算 $P_{W_{\tau }}(\phi )$ ，其为 $L_{\tau }$ 的最小值，即找到最短的映射就是将损失降到最小。虽然不能准确计算，但是我们可以使用梯度下降在某种程度上最小化这个损失。因此，在 reptile 中我们使用基于损失值从初始值 $\phi$ 开始的k 步梯度下降的结果代替 $W_{\tau }^{*}(\phi )$ 。