算法刷题之数组篇-二分查找法的原理及代码实现

力扣题目链接(opens new window)https://leetcode.cn/problems/binary-search/

1.1问题描述 -二分查找法

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4     

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1        

提示：

• 你可以假设 nums 中的所有元素是不重复的。
• n 将在 [1, 10000]之间。
• nums 的每个元素都将在 [-9999, 9999]之间。

1.2二分查找法适用场景

先划重点：二分法的适用场景很明确——有序数组 + 无重复元素。要是数组无序或有重复值，二分法要么用不了，要么找不出唯一答案。

接下来就讲最常用、最容易理解的一种写法：左闭右闭区间 [left, right] 即left<=right.

二分法各变量定义示意图

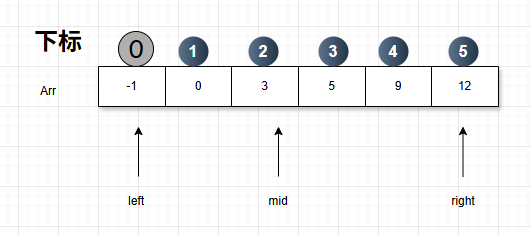
1.3左闭右闭区间 [left, right]的代码实现

先给区间下定义：target 一定在 [left, right] 这个范围里。这个定义直接决定了代码怎么写。

public class Solution {
    public int search(int[] Arr, int target) {
        int left = 0;
        int right = Arr.length - 1; // 定义target在左闭右闭的区间里，[left, right]
        
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2); // 防止溢出，等同于(left + right)/2
            
            if (Arr[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (Arr[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // Arr[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        
        // 未找到目标值
        return -1;
    }
}