模拟退火算法

声明：本文章内容仅代表个人观点！

本文讨论最大值的情况，最小值同理。

一、爬山法

在讲模拟退火算法之前，先说说爬山法。

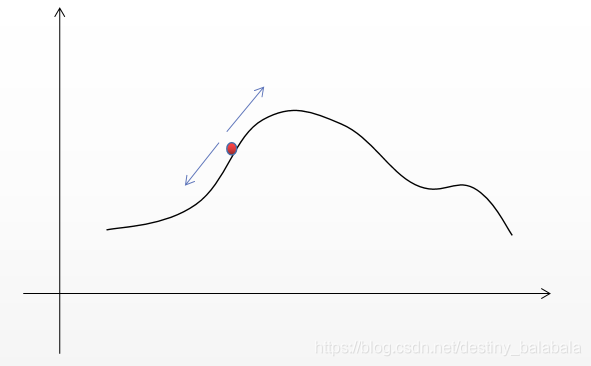
假设红点位置为当前解$A$，我们用$A$产生一个新解$B$。从图中可以看出$B$有两种情况$f(B)>f(A),f(B)<f(A)$。爬山法的思想就是：始终接受当前更优的解。由于是求最大值，所以爬山法会接受函数值较大的解$B$，即将$A$更新为$B$。然后用这个更优的解重复上述操作，直到迭代结束。

上面的这一段话可以换一种形式表达：
$$\{\begin{array}{ll}f(B)>f(A),& 以概率p=1接受新解B\\ f(B)<f(A),& 以概率p=0接受新解B\end{array}$$

存在的问题：显然，这种方法的局限性在于，容易搜索到极值，即局部最优解。其本质原因在于：该算法始终不接受$f(B)<f(A)$的新解$B$，所以如果靠近了局部最优解，会局限在局部最优解中。事实上，全局最优解有可能就在$f(B)<f(A)$的一侧。

二、模拟退火算法

模拟退火的思想就是：当出现$f(B)<f(A)$的情况时，并不是不接受它，而是以一定概率$p\in [0,1]$接受它。

$p$是如何确定的？

1. $p$的确定（1）

我们认为 ：当$f(A)$与$f(B)$更接近时，这个解更容易接受（可能说的有点没道理，暂时就这么写着吧。。）
所以：
$$p\propto \frac{1}{|f(A)-f(B)|}\in [0,1]$$

注意：这个仅表示反比关系，并不一定$p=C\ast \frac{1}{|f(A)-f(B)|}$。也有可能：$p=-C\ast |f(A)-f(B)|$。$C$为常数

2. $p$的确定（2）

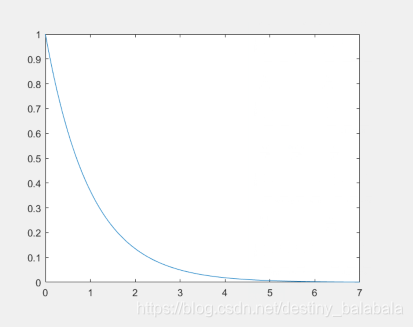
在已知的数学表达式中，有很多都满足这个。而模拟退火所选择的表达式为：$exp(-x),x\ge 0$，函数图像如下：

所以设：
$$p=exp(-|f(A)-f(B)|)$$

3. $p$的确定（3）

我们认为 ：在算法搜索初期，应该尽可能扩大搜索范围，这样才更有可能快速接近或找到全局最优解；而在搜索后期，基本接近最优解了之后，就可以缩小搜索范围了。这种思想有很符合实际情况，搜索的效率也比较高。

这种思想可以描述为：随着时间（或者是迭代次数的增加）的推移，$p$越来越小，即越来越不接受新解，搜索范围也就越来越小。所以可以将$p$的形式进一步改为：
$$p=exp(-|f(A)-f(B)|\ast C(t))$$

其中$C(t)$和时间$t$相关，且根据上述分析：$C(t)=g(t)$是递增函数。

4. $C(t)$的确定

实际上，到这一步才用到退火的思想。

模拟退火源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。（来自于百度百科）

那么温度是如何下降的呢？假设初始温度为$T_0$，则$t$时刻温度为：
$$T_t=\alpha \ast T_{t-1}={\alpha }^t\ast T_0$$

其中$\alpha$为常数，通常取0.95。
而模拟退火则令：
$$C(t)=\frac{1}{T_t}=\frac{1}{{\alpha }^t{T}_0}$$

取倒数是为了保证$C(t)$与$t$成正比关系。（$\alpha \in (0,1)$）

---

至此，$p$已确定完毕，表达式如下：
$$p=exp(-\frac{|f(A)-f(B)|}{{\alpha }^t{T}_0})$$

其中$\alpha ,T_0$为可调参数。

---

三、模拟退火算法说明

1. 算法流程图

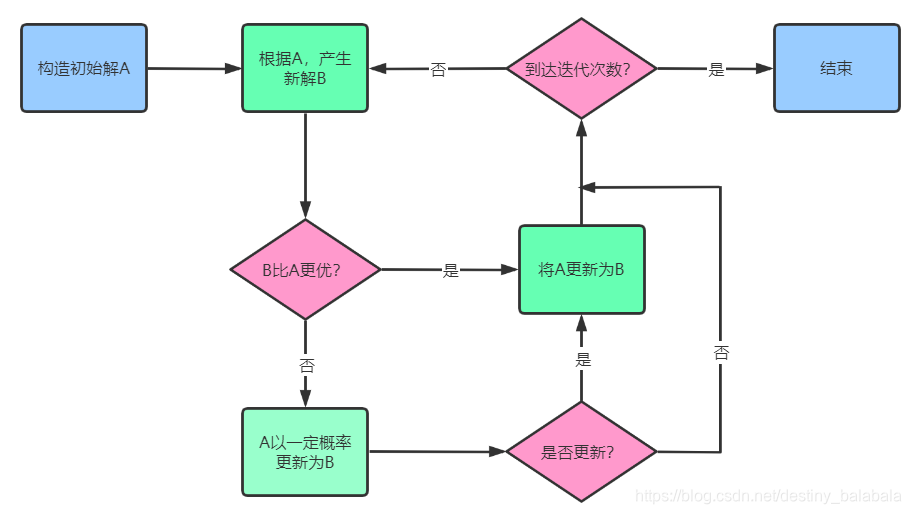
2. 产生新解$B$

产生新解$B$，方式有很多，碰到了在总结吧。。这里主要是想说一下：在迭代时间或者迭代次数的时候，每次迭代可以产生多个新解$B$，而不是一个，这样可以充分利用这次迭代，尽可能找到这次迭代的最优解。