[洛谷P3158] [CQOI2011]放棋子

洛谷题目链接:[CQOI2011]放棋子

题目描述

在一个m行n列的棋盘里放一些彩色的棋子，使得每个格子最多放一个棋子，且不同

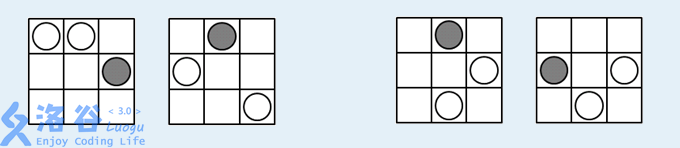
颜色的棋子不能在同一行或者同一列。有多少祌方法？例如，n=m=3,有两个白棋子和一

个灰棋子，下面左边两祌方法都是合法的，但右边两祌都是非法的。

输入输出格式

输入格式：

输入第一行为两个整数n, m, c，即行数、列数和棋子的颜色数。第二行包含c个正整数，即每个颜色的棋子数。所有颜色的棋子总数保证不超过nm。

输出格式：

输出仅一行，即方案总数除以 1,000,000,009的余数。

输入输出样例

输入样例#1：

4 2 2
3 1

输出样例#1：

8

说明

N,M<=30 C<=10 总棋子数<=250

题解: 一道\(DP\)的好题.

定义状态\(f[i][j][k]\)表示用前\(k\)种颜色占领了任意\(i\)行\(j\)列.

设\(a[k]\)表示第\(k\)种颜色的棋子的个数.

转移很显然是\[f[i][j][k]=\sum_{l=0}^{i-1}\sum_{r=0}^{j-1}f[l][r][k-1]*C_{n-l}^{i-l}*C_{m-r}^{j-r}*用a[k]个棋子占领任意i-l行j-r列的方案数\]

那么我们再定义状态\(g[i][j][k]\)表示用\(k\)个相同颜色的棋子占领任意\(i\)行\(j\)列的方案数,直接算不太好算,我们可以考虑容斥:\[g[i][j][k]=C_{i*j}^k-\sum_{l=0}^{i}\sum_{r=0}^{j}g[l][r][k]*C_{i}^{l}*C_{j}^{r},(l \not= i \ ||\ r \not= j)\]

预处理了\(g\)数组,就可以对\(f\)数组转移了:\[f[i][j][k]=\sum_{l=0}^{i-1}\sum_{r=0}^{j-1}f[l][r][k-1]*C_{n-l}^{i-l}*C_{m-r}^{j-r}*g[i-l][j-r][a[k]]\]

因为不一定要放满整个棋盘,所以\[ans=\sum_{l=1}^n\sum_{r=1}^mf[i][j][c]\]

其实还可以用滚动数组滚掉\(g\)数组的最后一维.

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
const int N = 30+5;
const int COL = 10+5;
const int K = 250+5;
const int mod = 1e9+9;

int n, m, C, a[N], c[1000][1000], ans = 0;
int f[N][N][COL], g[N][N][1000];
// f : k types of col occupied any i lines, j rows
// g : same type k chess piece occupied any i lines, j rows

int main(){
    cin >> n >> m >> C;
    for(int i = 1; i <= n; i++) cin >> a[i];
    f[0][0][0] = c[0][0] = 1;
    for(int i = 1; i <= 900; i++){
        c[i][0] = 1;
        for(int j = 1; j <= i; j++) c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod;
    }
    for(int k = 1; k <= C; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++){
                if(a[k] > i*j) continue; int res = 0;
                g[i][j][a[k]] = c[i*j][a[k]];
                for(int l = 1; l <= i; l++)
                    for(int r = 1; r <= j; r++)
                        if(l < i || r < j) (res += 1ll*c[i][l]*c[j][r]%mod*g[l][r][a[k]]%mod) %= mod;
                g[i][j][a[k]] = (g[i][j][a[k]]-res+mod)%mod;
            }
    for(int k = 1; k <= C; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
                for(int l = 0; l < i; l++)
                    for(int r = 0; r < j; r++)
                        (f[i][j][k] += 1ll*c[n-l][i-l]*c[m-r][j-r]%mod*g[i-l][j-r][a[k]]%mod*f[l][r][k-1]%mod) %= mod;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++) (ans += f[i][j][C]) %= mod;
    cout << ans << endl;
    return 0;
}

转载于:https://www.cnblogs.com/BCOI/p/10491544.html