函数递归调用_递归调用函数-优快云博客

本文链接：https://blog.youkuaiyun.com/demon_or_angle/article/details/117296366

本文介绍了Python函数递归的概念，包括直接和间接的递归调用，并指出Python为防止无限递归设置的限制。通过一个数学问题阐述了递归的回溯和递推阶段，强调递归必须有明确的结束条件。最后，提出了递归在解决某些问题时的实用性，并给出了一个递归应用的实践例子：遍历嵌套列表和查找有序数字列表中的目标数字。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

微信公众号搜索【程序媛小庄】，关注半路出家的程序媛如何靠python开发养家糊口~

引入

函数既可以嵌套定义也可以嵌套调用。嵌套定义指的是在定义一个函数时在该函数内部定义另一个函数；嵌套调用指的是在调用一个函数的过程中函数内部有调用另一个函数。而函数的递归调用指的是在调用一个函数的过程中又直接或者间接的调用该函数本身。

函数递归介绍

函数递归就是函数的递归调用，是函数嵌套调用的一种特殊形式，具体就是指在调用一个函数的过程中直接或者间接的调用到本身，递归的本质就是循环做重复的事情。

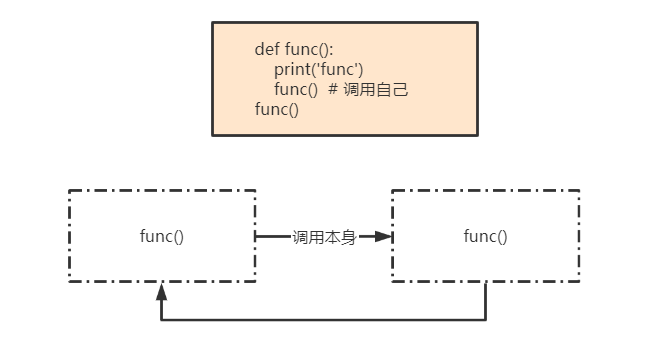
在调用func的过程中又调用func，这就是直接调用函数本身；

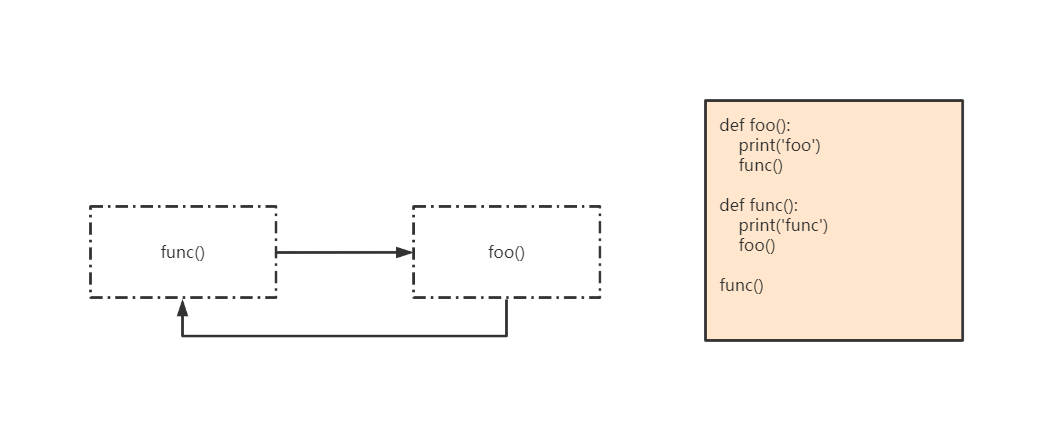
在调用func的过程中调用foo，而在调用foo的过程中又调用func，这就是间接调用func本身。

通过上面的分析，两种情况下的函数递归调用都是一个无限循环的过程，Python为了防止函数递归进入无限循环对函数递归调用的深度做了限制，一旦超出限制就会抛出异常。

def foo():
    print('foo')
    func()
def func():
    print('func')
    foo()

func()

'''
程序运行结果：
RecursionError: maximum recursion depth exceeded while calling a Python object(超过最大递归深度)
'''