基于QPDMLC电路的动态逻辑门与R-S触发器

基于准周期驱动Murali‐Lakshmanan‐Chua电路的动态逻辑门与R‐S触发器的设计与实现

P. R.文卡特斯1,a) A.文卡特斯安1,b)和 M.拉克希曼兰2,c)1尼赫鲁纪念学院（自治）物理系研究生部，普塔纳姆帕蒂，蒂鲁吉拉伯利 621007，印度 2巴拉提达桑大学物理学院非线性动力学中心，蒂鲁吉拉伯利 620 024，印度
（2016年10月21日收到；2017年2月20日接受；2017年3月6日在线发表）

我们报道了在准周期驱动穆拉里‐拉克希曼南‐楚阿（QPDMLC）电路系统中对方波信号的传播。观察发现，只有当方波或数字信号的强度超过某一阈值时，信号才能传播，所有高于该阈值幅度的范围被称为“信号传播区域”。随后，我们将此信号传播区域扩展用于执行各种逻辑运算，如与/与非/或/或非，因此该区域也被称为“逻辑操作区域”。基于这一区域，我们提出实现动态逻辑门，即与/与非/或/或非门，这些逻辑门可通过非对称输入方波决定，而无需改变系统参数。进一步地，我们表明单个QPDMLC系统能够同时产生两个互补的输出。因此，单个QPDMLC系统可同时实现与门和与非门，或或门和或非门。然后，我们将相应的两个QPDMLC系统以交叉耦合的方式连接，并发现其动力学行为类似于基本 R‐S触发器电路。上述所有现象均通过描述系统的电路方程的解析解进行了说明，最后将结果与相应的数值和实验分析进行了比较。

引言

近年来，基于非线性动力学的计算在理论上出现了新的研究方向。特别是，可以利用混沌现象实现灵活的计算。这种所谓的混沌计算范式旨在通过单个混沌单元来模拟不同的逻辑门，并最终构建更具动态性的架构。在这一方向上，辛哈和迪托的开创性工作基于阈值法（削波/限幅器）方法实现了不同的逻辑门。随后，普鲁沙和林德使用非线性参数化映射强调了非线性相较于混沌的重要性，并阐明了为何混沌与计算都依赖于非线性。在此基础上，穆拉里和辛哈提出了一种不同的方案，特别是利用驱动与响应非线性系统的同步来实现逻辑门操作。最近，穆拉里等人表明，适度噪声基底与非线性之间的相互作用可用于设计关键的逻辑门结构，称为逻辑随机共振（LSR）。随后，科哈尔等人进一步证明，噪声与周期性驱动相结合可在所有噪声强度下产生一致的逻辑门结构。他们还展示了通过对双稳态系统施加周期性强迫可实现无噪声逻辑随机共振。因此，基于非线性动力学的计算受到了广泛关注，并已在多种物理、化学和生物系统中得到验证。此外，许多近期的研究聚焦于利用非线性系统不仅作为逻辑门，而且作为存储器件的可能性。特别是，卡法尼亚和格拉西提出了由两个交叉耦合的NOR门实现的基于混沌的S‐R触发器单个李华电路。坎波斯‐坎顿等人报道了一种可重构的模拟模块，该模块能够基于分析几何学中的平面方程来模拟不同的逻辑门和S‐R触发器，并通过实验验证了其结果。柯哈尔和迪蒂纳展示了噪声如何使双稳态系统表现为置位‐重置锁存器以及逻辑门。王南和宋爱国在受有色噪声影响的对称双稳态系统中实现了置位‐重置锁存器的逻辑操作。除了逻辑门和存储器件外，坎波斯‐坎顿等人还提出了一种基于混沌李华电路系统的参数化方法，用于设计所有多谐振荡电路。这些作者已通过电子方式实现了全部多谐振荡电路、脉冲信号发生器以及完整的S‐R触发器器件。

最近，本文的两位作者描述了通过使用周期性强迫驱动分段线性非自治系统，利用逻辑振动共振(LVR)实现动态逻辑门的方法。在对一个周期驱动的非线性系统施加二次谐波扰动以展现振动共振现象时，人们发现：如果二次谐波力的频率与驱动力的频率是不可比的，则它们的比值将是无理数，并且可以在这些系统中发现奇异非混沌吸引子(SNAs)的存在。这类系统被称为准周期驱动非线性系统(QPDNSs)。尽管准周期驱动非线性系统普遍存在并广泛出现在众多物理和生物学情况中，但人们可以利用它们来传播信号，并使用某些非线性电路设计和实现动态逻辑门以及触发器操作。在SNA区域运行电路可以利用所需的非线性特性，而不会出现与混沌相关的邻近轨迹的指数分化。因此，可以在噪声环境下实现强健的基于非线性动力学的计算。据我们所知，迄今为止，文献中尚未使用表现出SNAs的准周期驱动非线性系统来实现基于非线性动力学的计算。本文中，我们首次利用准周期驱动 Murali‐Lakshmanan‐Chua(QPDMLC)电路系统来增强基于非线性动力学的计算。

在之前所有基于非线性动力学的计算研究中，两个需要进行逻辑运算的逻辑输入通常被视为通过电流源对方势坑施加的扰动，或被视为通过电压源施加的外部扰动，以构建逻辑门。除此之外，为了获得期望的逻辑行为，必须改变系统参数，或在表现出混沌同步、阈值机制和随机共振等现象的非线性系统中引入非对称偏置。最近，提出了一种新机制，通过在逻辑振动共振 Murali‐Lakshmanan‐Chua电路系统中对逻辑输入的高(1)和低(0)态施加约束条件，来实现动态逻辑门。在此机制中，无需改变系统参数或添加外部非对称偏置即可获得动态逻辑行为。因此，与其他技术相比，该方法更易于设计动态逻辑门，因为两个方波或数字信号的振幅将成为决定动态门的关键因素。

本文中，我们利用了当前作者中的两位提出的机制，并对其进行改进，以满足构建动态逻辑门所需的与/与非（AND/NAND）和或/或非（OR/NOR）门的条件。之所以要对上述机制进行修改，是因为在双参数相图中存在不同的选择性有界与门、或门和非门响应区域。因此，若要选择任意一种逻辑运算，不仅需要改变二次谐波力的振幅，还需要改变正电平或高电平输入逻辑信号的振幅。然而，在本文中无需如此，仅逻辑输入的不对称振幅就将成为决定不同逻辑行为的关键因素。这是因为在双参数相图中出现了分别对应与运算和或运算的选择性有界且相同的响应区域。除此之外，我们还发现单个QPDMLC系统能够逻辑地处理两个给定的逻辑输入，不仅可以通过x变量实现逻辑与或或运算，还能同时通过y变量提供其补运算，即与非或或非。因此，我们首次在一个电子电路中展示了逻辑门的并行实现。利用该电路固有的并行性，我们从两个交叉耦合的QPDMLC电路中获得了高电平有效的R‐S触发器和低电平有效的R‐S触发器。此类结果在以往的研究中均未被观察到。

然而，基于非线性动力学的计算的成功取决于给定的方波或数字信号在随机共振和振动共振等现象下被非线性系统传播的程度。考虑到这些因素，我们评估了 QPDMLC系统传播输入方波或数字信号所需的阈值幅度。阈值幅度以上的区域称为“信号传播区域”，该区域在双参数相图中进行了描绘。从信号传播区域中，我们确定了逻辑高电平或正峰值输入与逻辑低电平或负峰值输入的条件，以同时获得期望的与门/或门以及与非门/或非门行为。此外，我们进一步扩展这一思想，通过组合两个工作在与非门模式下的QPDMLC系统来实现基本 R‐S触发器，这更容易理解。所有这些现象都通过带有不可公约频率二次谐波驱动力的MLC电路归一化电路方程的分析解进行了解释，并将结果与使用四阶龙格‐库塔方法求解归一化电路方程得到的数值解进行了比较。因此，我们成功地设计出了所需的动态计算元件，即动态逻辑门和R‐S触发器，通过QPDMLC系统实现了这些功能而无需改变系统参数，并且能够证明逻辑高电平和低电平状态的幅度是决定动态计算的关键因素。

II. 准周期驱动Murali‐Lakshmanan‐Chua系统的电路实现

让我们考虑一个简单的电子电路，该电路对应于如图1所示的准周期驱动Murali‐Lakshmanan‐Chua（QPDMLC）电路系统。通过应用基尔霍夫定律，动力学方程可以表示如下：

$$
C \frac{dv}{dt} = i_L - g(v), \
L \frac{di_L}{dt} = -Ri_L - R_s i_L - v + f_1 \sin(\Omega_1 t) + f_2 \sin(\Omega_2 t),
$$

其中，$v$ 和 $i_L$ 分别表示非线性系统中电容 $C$ 两端的电压和通过电感 $L$ 的电流，而 $f_1$ 和 $f_2$ 分别表示频率为 $\Omega_1$ 和 $\Omega_2$ 的外部周期性电压源的强度。此处，$g(v)$ 表示系统中蔡氏二极管的分段线性特性函数：

$$
g(v) =
\begin{cases}
m_0 v + (m_0 - m_1)B_p, & v < -B_p, \
m_1 v, & -B_p \leq v \leq B_p, \
m_0 v + (m_1 - m_0)B_p, & v > B_p.
\end{cases}
$$

在公式中，$m_0$ 和 $m_1$ 分别是蔡氏二极管$(v-i)$特性曲线的内斜率和外斜率，$B_p$ 是区分 $(v-i)$曲线内斜率和外斜率的拐点。为了进行分析和数值验证，我们通过对变量重新定义对公式(1)进行重标度：$v = xB_p$；$i_L = yGB_p$；$G = 1/R$；$\omega_1 = \Omega_1 C/G$；$\omega_2 = \Omega_2 C/G$；$t = \tau C/G$ 以及 $\tau$ 为 $t$。重标度后得到的归一化方程组如下：

$$
\dot{x} = y - h(x), \quad (3a)\
\dot{y} = -\beta(1 + \delta)y - \beta x + F_1 \sin(\omega_1 t) + F_2 \sin(\omega_2 t), \quad (3b)
$$

其中，上方的点表示时间微分，

$$
h(x) =
\begin{cases}
bx + (a - b), & x > 1, \
ax, & |x| \leq 1, \
bx - (a - b), & x < -1,
\end{cases}
$$

$\beta = C/LG^2$；$\delta = GR_s$；$F_1 / 2 = f_1 / 2b/B_p$；$a = G_a/G$；$b = G_b/G$；$G_a = m_1 = -0.76\,\text{ms}$；$G_b = m_0 = -0.41\,\text{ms}$ 与 $B_p = 1\,\text{V}$。参数固定为 $a = -1.02$；$b = -0.55$；$\delta = 0.015$；$\beta = 1.0$；$\omega_1 = 2.0$。为了研究准周期激励下的系统，二次谐波力的频率保持为 $\omega_2 = \sqrt{5}-1/2$，以满足频率比 $\omega_1/\omega_2$ 为无理数的要求。上述系统的解析解$(3)$已在附录中简要讨论。

III. 方波信号在准周期驱动 Murali‐Lakshmanan‐Chua电路系统中的传播

为了传播数字信号，将一个电压源或由$I_0$表示的方波信号（在重新缩放后，在归一化方程中记为 $I$，$I = I_0 b/B_p$）与外部驱动力串联，如图2所示。应用基尔霍夫定律并进行重新缩放后，归一化方程组变为

$$
\dot{x} = y - h(x), \quad (5a)\
\dot{y} = -\beta(1 + \delta)y - \beta x + F_1 \sin(\omega_1 t) + F_2 \sin(\omega_2 t) + I. \quad (5b)
$$

相应的解由以下给出

$$
y(t) = C_{01}^{0,6} \exp(\alpha_1 t) + C_{02}^{0,6} \exp(\alpha_2 t) + E_1^0 + E_{12} \sin(\omega_1 t) + E_{13} \cos(\omega_1 t) + E_{22} \sin(\omega_2 t) + E_{23} \cos(\omega_2 t), \quad (6)
$$

and

$$
x(t) = \frac{1}{b}\left[-C_{01}^{0,6} (\alpha_1 + r) \exp(\alpha_1 t) - C_{02}^{0,6} (\alpha_2 + r) \exp(\alpha_2 t) + (E_{12}\omega_1 + E_{13}r) \cos(\omega_1 t) + (F_1 - E_{12}r + E_{13}\omega_1) \sin(\omega_1 t) + (E_{22}\omega_2 + E_{23}r) \cos(\omega_2 t) + (F_2 - E_{22}r + E_{23}\omega_2) \sin(\omega_2 t) - E_1^0 r + I\right], \quad (7)
$$

其中 $E_1^0 = \frac{lI + D}{B}$，积分常数变为

的Murali‐Lakshmanan‐Chua电路)

选择初始条件为 $x_0 = 0.2$；$y_0 = 0.3$，在 $t_0 = 0$ 时，固定 $F_1 = 0.08$。因此，对于 $F_2$ 在 $0$ 到 $0.2$ 范围内的不同取值，在 QPDMLC 系统(5) 中采用不同振幅 $(d)$ 的方波信号。通过使用公式(7)和(6)对系统(5)的解 $x$ 和 $y$ 进行分析发现，只有当方波信号的振幅 $(d)$ 达到临界值或高于该临界值时，QPDMLC 系统才会通过其状态变量 $x$ 和 $y$ 传播该信号。对于所有其他 $d$ 值（即低于固定 $F_2$ 值对应的临界值），系统的状态变量 $x$ 要么处于 $x > 0$（高电平状态）区域，要么处于 $x < 0$（低电平状态）区域，或处于双稳态区域。此外，系统的状态变量 $y$ 始终被发现与状态变量 $x$ 相互补。

不失一般性，对于随机输入方波或数字信号，逻辑高(1)状态取为$+d$，逻辑低(0)状态取为 $-d$。然后，利用公式(7)和(6)分析状态变量x和y的特性，并将其绘制在双参数相图中，如图3(a)和图3(b)所示。系统(5)的状态变量x模拟输入方波或数字信号，使得逻辑高输入在输出端表现为$x> 0$，逻辑低输入在输出端表现为$x < 0$。QPDMLC系统(5)对随机输入方波或数字信号的这种响应对应于图3(a)中双参数相图的红色区域。因此，该区域称为信号传播区域。另一方面，在图3(a)中，绿色区域对应逻辑输出响应 0−状态，即$x < 0$，蓝色区域对应逻辑输出响应 1−状态，即$x > 0$，而粉色区域对应双稳态（$x > 0$和$x < 0$），无论数字输入信号的状态如何。因此，在我们的讨论中，将QPDMLC系统输出状态$x$（或$y$）$< 0$解释为逻辑低输出0，将状态$x$（或$y$）$> 0$解释为逻辑高输出1。

另一方面，该系统的相应状态变量 $y$ 模拟了反向输入方波或数字信号，对应于红色区域，而绿色区域对应逻辑输出响应0−状态，即 $y < 0$，蓝色区域对应逻辑输出响应 1−状态，即 $y > 0$，且粉色区域对应于双稳态，与输入信号的逻辑状态无关，如图3(b)所示。

Numerical simulations of the system(5)采用四阶龙格‐库塔（RK IV）算法进行了数值模拟。系统对随机数字输入信号的不同响应（状态变量x和y）分别绘制为双参数相图，如图3(c)和3(d)所示，结果与解析结果完全一致。

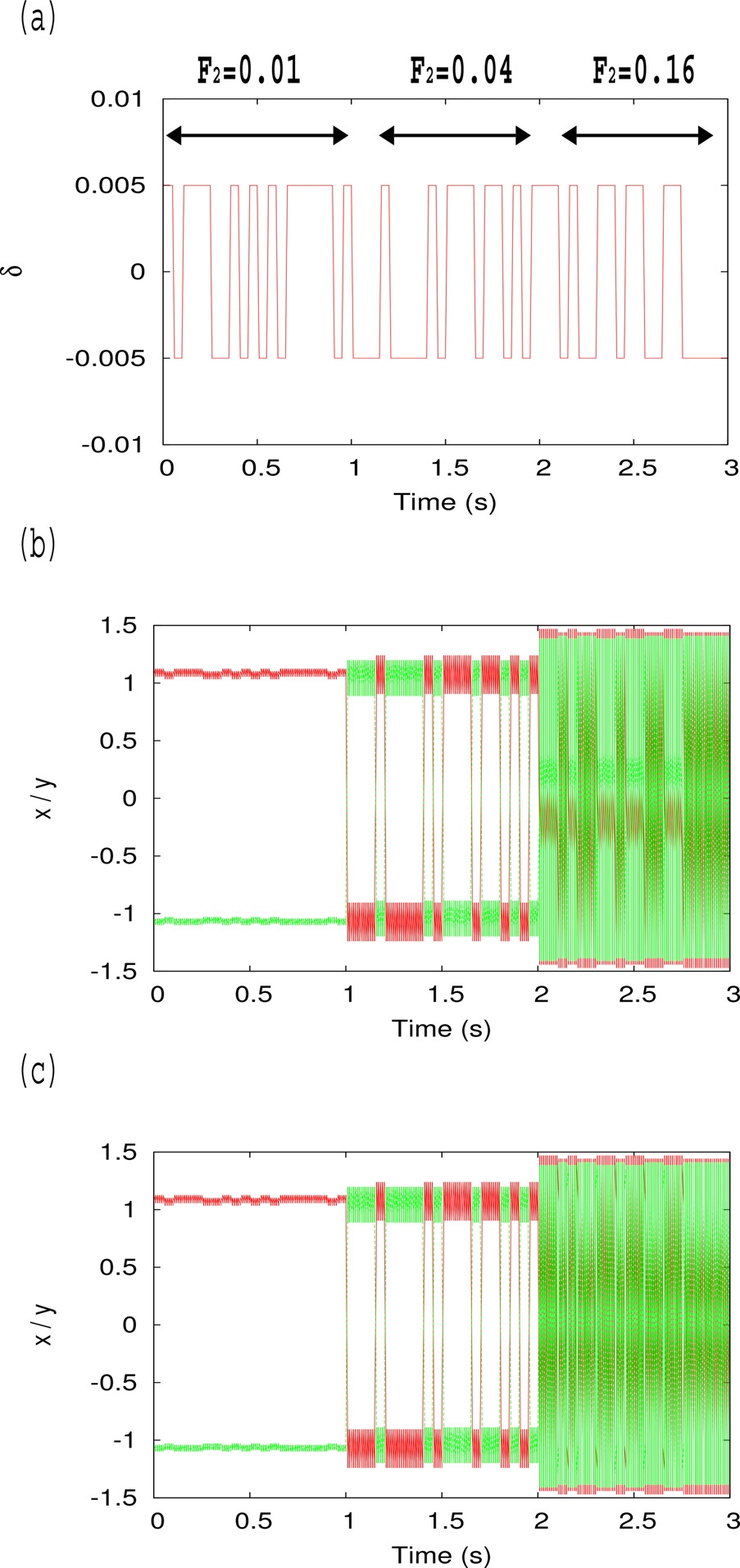
最后，通过在双参数相图的不同区域中选择不同时 间间隔下的$F_2$值，进一步验证了随机信号传播（见图 4(a)）在振幅$d = 0.006$时的上述行为。这些结果使用解析解绘制于图4(b)中（红线表示状态变量x，绿线表示状态变量y）。研究发现，在时间间隔 $[0: 1.0\,\text{s}]$内，当选择$F_2 = 0.01$时（对应于使用状态变量x时双参数相图中的蓝色区域（见图3(a)），以及使用状态变量y时的绿色区域（见图3(b)）），QPDMLC系统的状态变量x始终处于逻辑低电平状态（$x < 0$），而y处于逻辑高电平状态（$y > 0$），无论输入 $+d$或 $-d$的状态如何。另一方面，在时间间隔 $[1.0:2.0\,\text{s}]$内，当$F_2 = 0.04$时（对应图 3(a)和图3(b)中的红色区域），系统状态变量x跟随输入状态变化，证实了信号传播；而状态变量y则跟随输入的反向状态变化，证实了反向信号传播。随后，在时间间隔 $[2.0: 3.0\,\text{s}]$内，当$F_2 = 0.16$时（对应图3(a)和图 3(b)中的粉色区域），系统状态x和y处于双稳态。图 4(c)通过数值方法获得，也进一步确认了这些行为。

之间的相图，横轴为输入信号强度 d，纵轴为驱动力的振幅 F2，固定 F1 ＝ 0：08。(a) 和 (c) 分别表示通过分析解 （公式 (7)）和数值解得到的状态变量x对随机数字输入信号的响应；红色区域对应输入信号传播；绿色区域对应逻辑低态（x< 0），无论输入状态如何；蓝色区域对应逻辑高态（x> 0），无论输入状态如何；粉色区域对应双稳态（x> 0和 x< 0）。(b) 和 (d) 分别与 (a) 和 (c) 相同，但此处为y状态变量。)

的动态逻辑响应。（c）表示使用数值方法的系统(5)的动态逻辑响应。在区间:[0 : 1 0 2 ＝ 0] 01 [1 :s; F : 选择 在绿色区域；在区间: 0 : 2 0 2 ＝ 0 ] 04 [2 :s; F : 选择在红色区域；然后在区间: 0 : 3 0 2 ＝ 0 ] 16 :s; F : 选择在双 参数相图的蓝色区域。)

基于准周期驱动Murali‐Lakshmanan‐Chua电路的动态逻辑门与R‐S触发器的设计与实现

通过QPDMLC电路实现逻辑门

组合逻辑电路元件或逻辑门由奇异非混沌非线性系统构成，即带有外部不可公约频率驱动力和两个随机脉冲电压源 $I_0^1$ 和 $I_0^2$ 的MLC系统，而不是如图2所示的单个电压源 $I_0$。正如文卡特斯安等所指出，在基于非线性动力学的计算讨论中，通过选择 $F_1 = 0.08$ 和 $F_2 = 0.07454785$，将QPDMLC电路系统的参数设置为表现出奇异非混沌吸引子（SNA）。$I_1$ 和 $I_2$ 这两个电压源即用于此目的，并且在重新缩放后，它们将变为 $I_1 + I_2$ 而不是 $I$ 在公式 (5b) 和 (6)–(9) 中分别表示的。

利用这些输入信号，四种可能的输入组合 $(0, 0)$、$(0, 1)$、$(1, 0)$ 和 $(1, 1)$ 被合并为三种不同的输入组合 $(0, 0)$、$(0, 1)/(1, 0)$ 和 $(1, 1)$。低电平输入取为 $-1$ 表示逻辑0，高电平输入取为 $-2$ 表示逻辑1。不失一般性，设两个输入 $I_1$ 和 $I_2$ 在逻辑输入为0时取值为 $-1$，在逻辑输入为1时取值为 $-2$。然后，这两个逻辑输入通过与门或或门的方式进行不同组合的逻辑相加，从而得到结果：要么是逻辑低输出0（对应于小于或等于 $-d_T$ 的值），要么是逻辑高输出1（对应于大于或等于 $d_T$ 的值）。$d_T$ 的极性指明系统处于正势阱或负势阱中。此外，$d_T$ 是将在第三节讨论的QPDMLC系统中传播的数字输入信号的振幅。因此，$d_T$ 和 $F_2$ 的值将始终选择在QPDMLC系统的信号传播区域（即对应于状态变量 $x$ 的双参数相图中的红色区域，即图3(a)中的红色区域）内。令系统参数选择为 $d_T = 0.05$ 和 $F_2 = 0.07454785$。这是因为只有该区域内的参数才能使QPDMLC系统对给定的两个输入进行逻辑相加，最终产生类似于与门或或门操作的输出。因此，该区域也可称为“逻辑操作区域”。基于上述考虑，三种可能的输入组合将以与门或或门方式进行逻辑相加，且结果必须满足信号传播条件（即结果 $d_T$ 的值必须位于对应于状态变量 $x$ 的双参数相图的红色区域、信号传播区域或逻辑操作区域内），如下所示：

与门

$$
-1 + (-1) \leq -d_T, \quad (10a) \
-1 + (-2) \leq -d_T, \quad (10b) \
-2 + (-2) \geq d_T. \quad (10c)
$$

由式(10c)可得，$-2 \geq d_T/2$。代入式(10b)后，$-1 \leq -3d_T/2$ 也满足式(10a)。因此

$$
-1 \leq -\frac{3d_T}{2}, \quad (11a) \
-2 \geq \frac{d_T}{2}, \quad (11b)
$$

是与运算的条件。

或门

$$
-1 + (-1) \leq -d_T, \quad (12a) \
-1 + (-2) \geq d_T, \quad (12b) \
-2 + (-2) \geq d_T. \quad (12c)
$$

根据公式 (12c)，$-2 \geq 3d_T/2$；将上式代入公式 (12b)，同样满足公式 (12a)。因此

$$
-1 \leq -\frac{d_T}{2}, \quad (13a) \
-2 \geq \frac{3d_T}{2}, \quad (13b)
$$

是或运算的条件。

以一个例子为例，让我们在图3(a)所示的双参数相图的传播区域（红色区域）中固定参数，$F_1 = 0.08$；$F_2 = 0.07454785$，以及 $d_T = 0.05$。结果，根据公式(11)，输入信号的低态（$-1$）和高态（$-2$）分别变为 $-1 = -0.075$ 和 $-2 = 0.025$，用于与/与非运算。类似地，公式 (13) 给出 $-1 = -0.025$ 和 $-2 = 0.075$，分别用于或/或非运算。利用这些值，对于各种逻辑输入组合 $(-1, -1)$；$(-1, -2)$；$(-2, -1)$, 和 $(-2, -2)$, QPDMLC系统的状态变量 $x$ 同时模拟与门，$y$ 模拟与非门运算，如图5所示。类似地，对于 $-1 = -0.025$ 和 $-2 = 0.075$ 的各种组合，该系统表现出或门和或非门响应，如图6所示。

对应持续1.0秒的随机输入信号I 1 和I 2 ；(b) 实际的与门输出（1表示高电平状态，−1表示低电平状态）；(c) 表示使用解析解时系统(5)的动态逻辑响应；(d) 表示使用数值方法时系统(5)的动态逻辑响应。在区间[0: 1:0s]内，状态变量x模拟与运算，变量y模拟与非运算。)

A. 实验研究

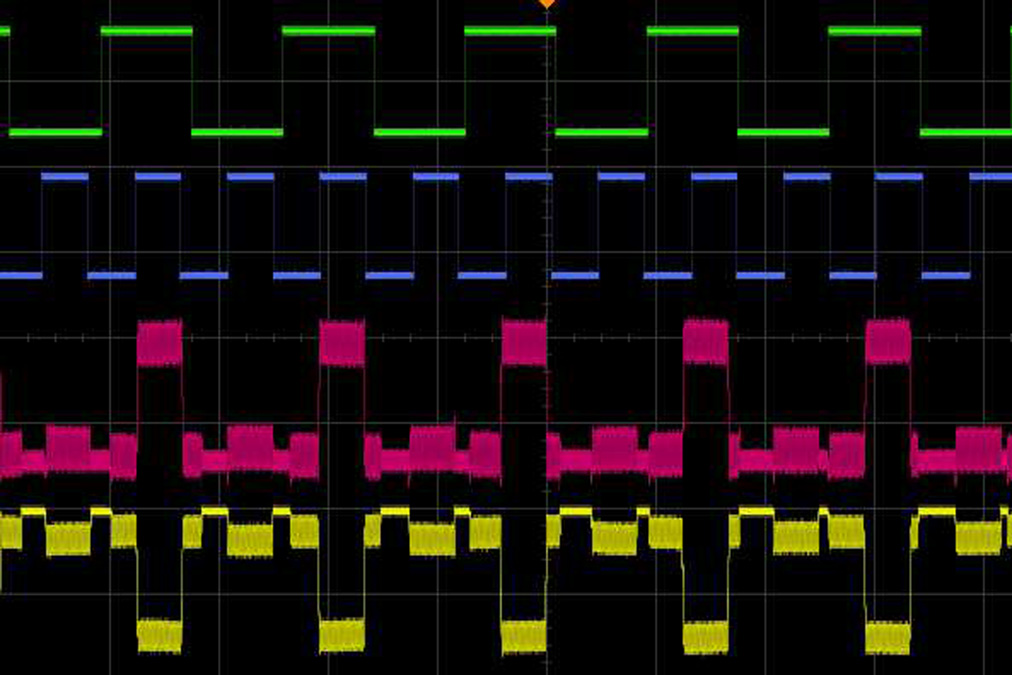
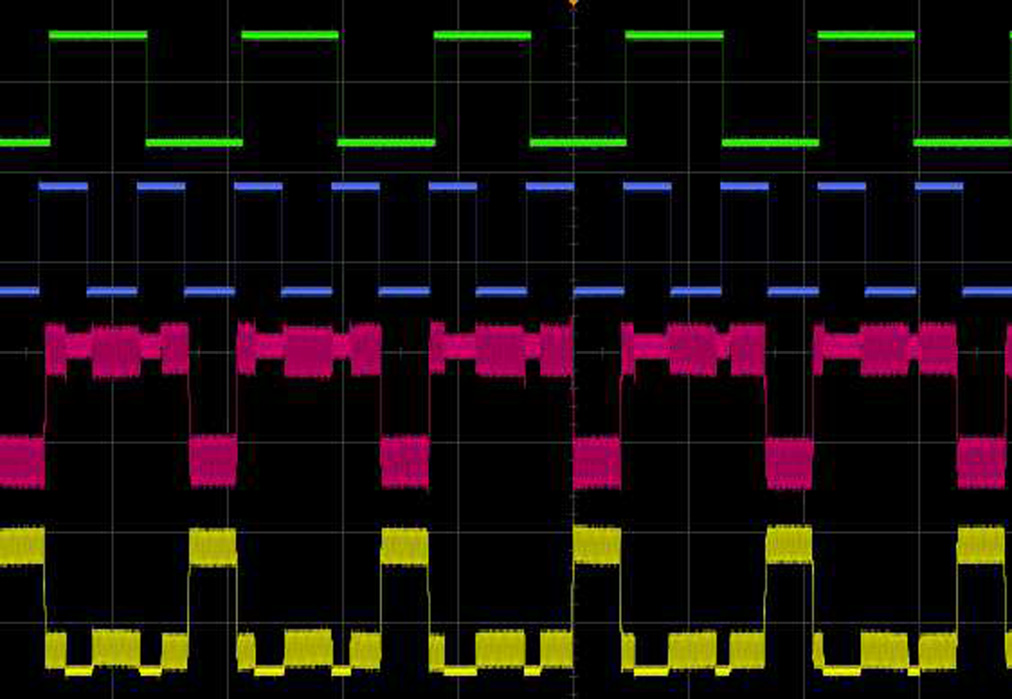
QPDMLC系统（即带有外部不可公约频率驱动力的MLC系统）在引入两个方波输入 $I_0^1$ 和 $I_0^2$ 而非单一输入方波 $I_0$ 时的动力学行为已通过实验进行研究，如图2所示。为了通过实验验证图2所示电路的数值结果，将电路参数设定为上述数值研究中所使用的无量纲参数对应的值：$C = 10\,\text{nF}$，$L = 18\,\text{mH}$，$R = 1340\,\Omega$，$R_s = 20\,\Omega$，$f_1 (= \Omega_1 / 2\pi) = 23706.667\,\text{Hz}$ 和 $f_2 (= \Omega_2 / 2\pi) = 7325.763\,\text{Hz}$；$f_1 = 0.056572\,\text{V} {\text{rms}}$ 以及 $f_2 = 0.05270\,\text{V} {\text{rms}}$。对于这组系统参数值，此前已观察到该电路表现出奇异的非混沌行为。现在，在两个输入 $I_0^1$ 和 $I_0^2$ 的作用下，通过测量电容“C”两端的电压“v”以及电感“L”中的电流 $i_L$（以电流检测电阻“$R_s$”上的电压降形式表示，即 $v_s = R_s i_L$），可以获得吸引子时间序列的变化。两个输入信号 $I_0^1$ 和 $I_0^2$ 以及电压“v”和“$v_s$”分别连接至安捷伦混合存储示波器(MSO‐X 3014A)的通道1、2、3和4。随后，对于两组适当的非对称输入方波，QPDMLC系统在“v”变量中表现出与门特性，在“$v_s$”变量中表现出与非门特性（见图7）。而对于另一组适当的非对称输入方波，该系统在测量“C”两端电压时表现为或门，在测量“$R_s$”两端电压时表现为或非门（见图8）。因此，与门和与非门以及或门和或非门的并行性内置于QPDMLC电路之中，有助于更快地执行逻辑运算。

V. 通过QPDMLC电路实现R‐S触发器

接下来，我们考虑两个模拟与门/与非门的量子点忆阻逻辑电路系统，它们通过耦合构成时序逻辑电路的基本单元，称为触发器电路。因此，表征高电平有效以及低电平有效的R‐S触发器的两个耦合量子点忆阻逻辑电路系统表示如下：

$$
\dot{x}_1 = y_1 - h(x_1), \
\dot{y}_1 = -\beta(1 + \delta)y_1 - \beta x_1 + F_1 \sin(\omega_1 t) + F_2 \sin(\omega_2 t) + S + I(y_2), \
\dot{x}_2 = y_2 - h(x_2), \
\dot{y}_2 = -\beta(1 + \delta)y_2 - \beta x_2 + F_1 \sin(\omega_1 t) + F_2 \sin(\omega_2 t) + R + I(y_1),
\quad (14)
$$

其中

$$
I(y_{1,2}) =
\begin{cases}
\frac{3y_{1,2}}{2}, & y_{1,2} < 0, \
\frac{y_{1,2}}{2}, & y_{1,2} > 0.
\end{cases}
$$

上述特征方程的解被发现与单个QPDMLC系统的解相似，只需分别将常数 $I$ 修改为 $R + I(y_1)$ 和 $S + I(y_2)$ 即可。因此，通过在公式(7)和(6)中分别将 $I$ 替换为 $S + I(y_2)$ 和 $R + I(y_1)$，即可得到解 $x_{1,2}$ 和 $y_{1,2}$，并且可以绘制出如图9(b)所示的耦合系统(14)的响应。在此，我们将 $y_1$ 解释为 R‐S触发器 的输出Q，将 $y_2$ 解释为输出 $\bar{Q}$。同时，状态变量 $y_{1,2} > 0$ 被视为逻辑高输出，$y_{1,2} < 0$ 被视为逻辑低输出。最后，高电平有效R‐S触发器 的各种操作描述如下：

1. 当S和R输入均为 $-1 = -0.075$ 或低电平时，输出 $y_1$ 和 $y_2$ 同时变为逻辑低(0)或 $y_{1,2} < 0$。这表示触发器的禁止状态。

2. 当S为 $-1 = -0.075$ 或低电平，且R为 $-2 = 0.025$ 或高电平时，$y_1$ 输出被置为逻辑高(1)或 $y_1 > 0$，且 $y_2$ 输出被复位或清零为低电平(0)或 $y_2 < 0$。这模拟了置位条件。

3. 当S为 $-2 = 0.025$ 或高电平，R为 $-1 = -0.075$ 或低电平时，$y_1$ 输出被复位为逻辑低(0)或 $y_1 < 0$，而 $y_2$ 输出被置为高(1)或 $y_2 > 0$。这模拟了复位条件。

4. 当S和R输入均为 $-2 = 0.025$ 或高电平时，耦合的 QPDMLC系统使输出 $y_1$ 和 $y_2$ 保持在先前的互补状态。这表明了保持或空闲或静止或记忆效应的条件。

类似地，状态变量 $x_1$ 作为 $Q’$ 和 $x_2$ 作为 $\bar{Q’}$ 的响应如图10(b)所示，该电路被定义为低电平有效R‐S触发器。发现状态变量 $x_{1,2}$ 的置位和复位条件互换了。上述结果通过龙格‐库塔四阶方法进行了数值验证，并分别在图9(c)和10(c)中绘制了状态变量 $y_{1,2}$ 和 $x_{1,2}$ 的波形。

的动态逻辑响应；（c） 表示通过数值方法获得的耦合QPDMLC系统(14)的动态逻辑响应。状态变量y1模拟R‐S触发器的Q输出，状态变量y2模拟 Q输出。S表示 置位Q＝ 1和 Q＝ 0，R表示复位Q＝ 0和 Q＝ 1，F表示禁止状态，即Q和 Q同时存在于同一状态，H表示保持前一状态不变。)

VI. 结论

总之，我们推导出了准周期驱动 Murali‐Lakshmanan‐Chua系统模拟动态逻辑门和基本R‐S触发器的方程，并给出了精确解析解。此外，我们证明了在双参数相图中被称为信号传播区域的某些区域内，方波或数字信号可以在准周期驱动的 Murali‐Lakshmanan‐Chua电路系统中实现传播。我们将这一信号传播的思想进一步拓展，用于构建组合逻辑电路的基本构建模块，即逻辑门，以及时序逻辑电路的基本构建模块，即触发器。特别地，通过合理选择被定义为不对称输入信号的逻辑高电平和逻辑低电平输入值，我们展示了利用QPDMLC系统直接且灵活地实现所需的OR/或非门以及与/与非门。这些输入信号正态和负态的不对称幅值是通过在信号中使用参数 $d$ 和 $F_2$ 对与门和或门的条件获得的双参数相图的传播区域。随后，我们扩展了这一思想，在与/与非条件下结合两个准周期驱动MLC系统，同时实现了高电平有效R‐S触发器和低电平有效R‐S触发器。所有这些行为均通过解析方法进行研究，并通过数值结果加以验证。这些逻辑门还通过实验得以实现。结论表明，所有这些动态计算均在不改变系统参数的情况下完成，而是依赖于输入方波信号的不对称幅值。这种用于数字电路的基本动态逻辑门和触发器的实现方案，可作为通用设备的组成部分，比静态布线硬件更加灵活。